[C++知识库]如何用C语言做离散傅里叶变化

1 离散傅里叶变换

此图大家都再熟悉不过了，任何周期信号都可以看作是一系列不同频率正弦信号叠加的结果。

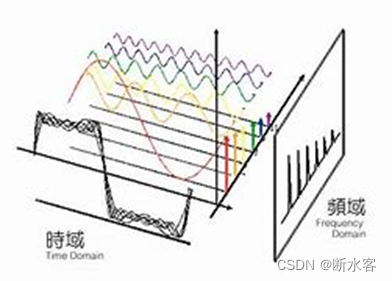
信号从时域变换到频域的过程，可以借助傅里叶变换（Fourier transform）完成。我们知道连续信号的傅里叶变换是一个积分过程，而处理连续信号并不是计算机所擅长的，通常是处理离散的采样信号。

物理信号的数字采样结果是含有N个点的点集，用x[n]，（n=1，2，…N）表示。对点集x[n]做的傅里叶变换，即本文要介绍的离散傅里叶变化（DFT，Discrete Fourier Transform）。

2 理解DFT的表达式

在看离散傅里叶变换的数学表达式之前，咱先认识一下频谱图。下面这张图横坐标是频率，纵坐标是权值，此图显示了某一信号中不同频率成分的权值情况。

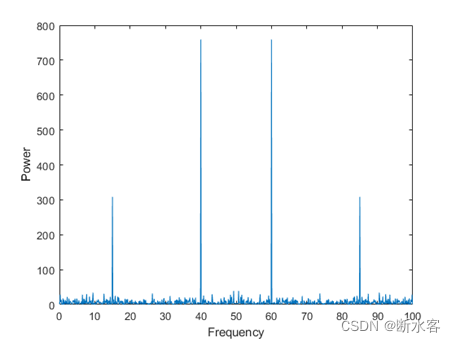
我们对信号做傅里叶变换，主要目的也就是想得到它的频谱图，也就是计算出每个频点对应的权值（或者不同频率成分的正弦信号的幅值）。

离散傅里叶变换的数学表达式如下

${\sum }_{n=0}^{N?1}x[n]W_N^{kn}$

其中N是采样点数量。

可以看到，等式左边是一个复数，等式右边是一个求和结果。此式可以这样理解——对于离散信号x[n]而言，他的第k个频率分量的复数形式$X[k]$是$x[n]W_N^{kn}$在整数n从0变化到N-1过程中得到的所有值求和的结果。也就是说，频谱图的横坐标为k的位置上竖线的高度就是$X[k]$的模（复数的模）。

所以只要能够计算出$x[n]W_N^{k}n$，就能得到第k个$X[k]$，进而也就能得到信号的频谱啦。那么怎去计算这些值呢？我们知道x[n]就是原信号的采样点，那$W_N^{k}n$是什么呢？

它是一个简写，实际上

$W_N^{kn}=e^{\frac{?j2kn}{N}}$

把它放到最开始那个公式里面，我们就得到

$X[k]={\sum }_{n=0}^{N?1}x[n](e^{\frac{?j2kn\Pi }{N}})$

求和符号里面就剩下两部分，一部分是原始信号，另一部分是$e^{\frac{?j2kn\Pi }{N}}$。

这样似乎足够了，用上面这个公式就可以得到$X[k]$，但是咱每次都得做$e$的指数运算，似乎不太好。我们可以用欧拉公式把指数计算换成正余弦求和运算。

$X[k]={\sum }_{n=0}^{N?1}x[n]cos?(\frac{2kn\Pi }{N})〗+j?{\sum }_{n=0}^{N?1}x[n]sin?(\frac{2kn\Pi }{N})$

这样我们可以通过求各点参数对应的正余弦函数得到该点的傅里叶变换结果。同时要记得计算的结果是一个复数——因为余弦部分对应实部，正弦部分对应虚部，我们可以用两部分的平方和计算出$X[k]$的模值。

$幅值=\sqrt{实{部}^2+虚{部}^2}$

$相位=arctan(\frac{虚部}{实部})$

上述这些计算都会在代码中体现。

3 用代码表达

Talk is free， show code please.

从上一节知道，某个频点的傅里叶变换可以分为正弦求和和余弦求和两部分，这两个计算过程分别用下面这两个函数来完成。

/* 傅里叶变换中的正弦求和过程 */
void cosComponent(double* transmitted, double* sample, int sampleSize);
/* 傅里叶变换中的余弦求和过程 */
void sinComponent(double* transmitted, double* sample, int sampleSize);

它们都是输入样本数据和样本数量，把计算结果保存到transmitted这个指针参数对应的空间中。定义如下

/* 计算余弦分量
	@param transmitted,计算得到的一系列余弦分量
	@param sample，采样数据样本
	@param sampleSize，样本数
	@retVal None
*/
void cosComponent(double* transmitted, double* sample, int sampleSize)
{
	memset(transmitted, 0, sampleSize);
	for (int k = 0;k < sampleSize;k++)
		for (int n = 0;n < sampleSize;n++) {
			transmitted[k] += sample[n] * cos((2 * PI * k * n) / (double)sampleSize);
		}
}

/* 计算正弦分量
	@param transmitted，计算得到的一系列正弦分量
	@param sample，采样数据样本
	@param sampleSize，样本数
	@retval None
*/
void sinComponent(double* transmitted, double* sample, int sampleSize)
{
	memset(transmitted, 0, sampleSize);
	for (int k = 0;k < sampleSize;k++)
		for (int n = 0;n < sampleSize;n++) {
			transmitted[k] += sample[n] * sin((2 * PI * k * n) / (double)sampleSize);
		}
}

有了上面这两个函数，咱就可以完成傅里叶变换了

/* 快速傅里叶变换
	@param cosComponent,计算得到的余弦分量
	@param sinComponent，计算得到的正弦分量
	@param sample,样本
	@param sampleSize，样本数
*/
void Fast_Fourier_Transform(double* cosComponent, double* sinComponent, double* sample, int sampleSize)
{
	memset(cosComponent, 0, sampleSize);
	memset(sinComponent, 0, sampleSize);
	for (int k = 0;k < sampleSize;k++)
		for (int n = 0;n < sampleSize;n++) {
			cosComponent[k] += sample[n] * cos((2 * PI * k * n) / (double)sampleSize);
			sinComponent[k] += sample[n] * sin((2 * PI * k * n) / (double)sampleSize);
		}
}

正余弦求和部分的计算结果分别对应复数结果的实部和虚部，得到它们之后可以用来求各频率分量的幅值和相位，同时可以结合采样率计算得到频谱图的横轴坐标。

/* 幅值计算 */
void amplitudeCaculate(double* amplitudes, double* cosComponent, double* sinComponent, int sampleSize);
/* 相位计算 */
void PhaseCalculate(double* phase, double* cosComponent, double* sinComponent, int sampleSize);
/* 频率计算，计算频谱图的横轴坐标 */
void frequencyCaculate(double* frequency, double sampleRate, int sampleSize);

输出频谱的流程如下，先计算得到各点的傅里叶变换，然后计算各点的幅值和相位。

/* 样本数据 */
double sample[] = {
	1,1.10749098133538,1.11803398874990,1.04177575203202,0.896802246667421,0.707106781186548,0.500000000000000,0.303221271895895,0.142039521920206,0.0366318242999842,0,0.0366318242999841,0.142039521920206,0.303221271895895,0.500000000000000,0.707106781186547,0.896802246667421,1.04177575203202,1.11803398874990,1.10749098133538,1.00000000000000,0.794622051254923,0.500000000000000,0.133794752552927,-0.278768257917525,-0.707106781186547,-1.11803398874989,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648084,-1.11803398874990,-0.707106781186546,-0.278768257917526,0.133794752552926,0.500000000000000,0.794622051254922,1.00000000000000,1.10749098133538,1.11803398874990,1.04177575203202,0.896802246667421,0.707106781186548,0.500000000000000,0.303221271895894,0.142039521920206,0.0366318242999842,0,0.0366318242999845,0.142039521920206,0.303221271895895,0.500000000000000,0.707106781186548,0.896802246667420,1.04177575203202,1.11803398874990,1.10749098133538,1.00000000000000,0.794622051254925,0.500000000000001,0.133794752552925,-0.278768257917525,-0.707106781186549,-1.11803398874989,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648084,-1.11803398874990,-0.707106781186551,-0.278768257917527,0.133794752552927,0.499999999999999,0.794622051254923,1.00000000000000,1.10749098133538,1.11803398874989,1.04177575203202,0.896802246667421,0.707106781186549,0.500000000000001,0.303221271895896,0.142039521920207,0.0366318242999840,0,0.0366318242999842,0.142039521920206,0.303221271895895,0.500000000000002,0.707106781186548,0.896802246667420,1.04177575203202,1.11803398874989,1.10749098133539,1.00000000000000,0.794622051254922,0.499999999999998,0.133794752552930,-0.278768257917524,-0.707106781186539,-1.11803398874990,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648085,-1.11803398874989,-0.707106781186552,-0.278768257917518,0.133794752552918,0.499999999999995,0.794622051254920,0.999999999999999,1.10749098133538,1.11803398874990,1.04177575203202,0.896802246667421,0.707106781186548,0.499999999999999,0.303221271895897,0.142039521920207,0.0366318242999841,0,0.0366318242999834,0.142039521920202,0.303221271895895,0.499999999999997,0.707106781186550,0.896802246667416,1.04177575203202,1.11803398874989,1.10749098133538,1.00000000000000,0.794622051254923,0.500000000000006,0.133794752552931,-0.278768257917523,-0.707106781186548,-1.11803398874989,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648084,-1.11803398874989,-0.707106781186553,-0.278768257917528,0.133794752552926,0.500000000000002,0.794622051254920,0.999999999999999,1.10749098133538,1.11803398874989,1.04177575203202,0.896802246667418,0.707106781186552,0.500000000000004,0.303221271895897,0.142039521920207,0.0366318242999841,0,0.0366318242999832,0.142039521920205,0.303221271895895,0.499999999999996,0.707106781186545,0.896802246667420,1.04177575203202,1.11803398874990,1.10749098133539,1.00000000000000,0.794622051254923,0.499999999999999,0.133794752552922,-0.278768257917523,-0.707106781186547,-1.11803398874989,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648085,-1.11803398874990,-0.707106781186553,-0.278768257917529,0.133794752552926,0.499999999999994,0.794622051254919,0.999999999999999
};
/* 样本相关参数
	@sampleSize：样本长度，即样本中数值的个数
	@sampleWidth：采样宽度，即采样区间的时间长度，以秒为单位
	@sampleRate：采样率，单位时间内采样的次数，=样本长度/采样宽度(次/秒)
*/
const int sampleSize = 201;
const int sampleWidth = 1;
const int sampleRate = sampleSize/sampleWidth;

int main()
{
	/* 计算结果容器 */
	double cosComponent[sampleSize] = { 0 };
	double sinComponent[sampleSize] = { 0 }; 
	double amplitudes[sampleSize] = { 0 };
	double phases[sampleSize] = { 0 };
	double frequencies[sampleSize] = {0};
	/* 快速傅里叶变换 */
	Fast_Fourier_Transform(cosComponent, sinComponent,sample,sampleSize);
	/* 计算序列号对应的频点 */
	frequencyCaculate(frequencies,sampleRate,sampleSize);
	/* 计算各频点幅值 */
	amplitudeCaculate(amplitudes, cosComponent, sinComponent, sampleSize);
	/* 计算各频点的相位 */
	PhaseCalculate(phases,cosComponent,sinComponent,sampleSize);
}

这部分是测试数据和参数

/* 样本数据 */
double sample[] = {
	1,1.10749098133538,1.11803398874990,1.04177575203202,0.896802246667421,0.707106781186548,0.500000000000000,0.303221271895895,0.142039521920206,0.0366318242999842,0,0.0366318242999841,0.142039521920206,0.303221271895895,0.500000000000000,0.707106781186547,0.896802246667421,1.04177575203202,1.11803398874990,1.10749098133538,1.00000000000000,0.794622051254923,0.500000000000000,0.133794752552927,-0.278768257917525,-0.707106781186547,-1.11803398874989,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648084,-1.11803398874990,-0.707106781186546,-0.278768257917526,0.133794752552926,0.500000000000000,0.794622051254922,1.00000000000000,1.10749098133538,1.11803398874990,1.04177575203202,0.896802246667421,0.707106781186548,0.500000000000000,0.303221271895894,0.142039521920206,0.0366318242999842,0,0.0366318242999845,0.142039521920206,0.303221271895895,0.500000000000000,0.707106781186548,0.896802246667420,1.04177575203202,1.11803398874990,1.10749098133538,1.00000000000000,0.794622051254925,0.500000000000001,0.133794752552925,-0.278768257917525,-0.707106781186549,-1.11803398874989,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648084,-1.11803398874990,-0.707106781186551,-0.278768257917527,0.133794752552927,0.499999999999999,0.794622051254923,1.00000000000000,1.10749098133538,1.11803398874989,1.04177575203202,0.896802246667421,0.707106781186549,0.500000000000001,0.303221271895896,0.142039521920207,0.0366318242999840,0,0.0366318242999842,0.142039521920206,0.303221271895895,0.500000000000002,0.707106781186548,0.896802246667420,1.04177575203202,1.11803398874989,1.10749098133539,1.00000000000000,0.794622051254922,0.499999999999998,0.133794752552930,-0.278768257917524,-0.707106781186539,-1.11803398874990,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648085,-1.11803398874989,-0.707106781186552,-0.278768257917518,0.133794752552918,0.499999999999995,0.794622051254920,0.999999999999999,1.10749098133538,1.11803398874990,1.04177575203202,0.896802246667421,0.707106781186548,0.499999999999999,0.303221271895897,0.142039521920207,0.0366318242999841,0,0.0366318242999834,0.142039521920202,0.303221271895895,0.499999999999997,0.707106781186550,0.896802246667416,1.04177575203202,1.11803398874989,1.10749098133538,1.00000000000000,0.794622051254923,0.500000000000006,0.133794752552931,-0.278768257917523,-0.707106781186548,-1.11803398874989,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648084,-1.11803398874989,-0.707106781186553,-0.278768257917528,0.133794752552926,0.500000000000002,0.794622051254920,0.999999999999999,1.10749098133538,1.11803398874989,1.04177575203202,0.896802246667418,0.707106781186552,0.500000000000004,0.303221271895897,0.142039521920207,0.0366318242999841,0,0.0366318242999832,0.142039521920205,0.303221271895895,0.499999999999996,0.707106781186545,0.896802246667420,1.04177575203202,1.11803398874990,1.10749098133539,1.00000000000000,0.794622051254923,0.499999999999999,0.133794752552922,-0.278768257917523,-0.707106781186547,-1.11803398874989,-1.47879177648084,-1.76007351067010,-1.93874485689029,-2,-1.93874485689029,-1.76007351067010,-1.47879177648085,-1.11803398874990,-0.707106781186553,-0.278768257917529,0.133794752552926,0.499999999999994,0.794622051254919,0.999999999999999
};
/* 样本相关参数
	@sampleSize：样本长度，即样本中数值的个数
	@sampleWidth：采样宽度，即采样区间的时间长度，以秒为单位
	@sampleRate：采样率，单位时间内采样的次数，=样本长度/采样宽度(次/秒)
*/
const int sampleSize = 201;
const int sampleWidth = 1;
const int sampleRate = sampleSize/sampleWidth;

根据计算输出绘制的频谱如下图所示

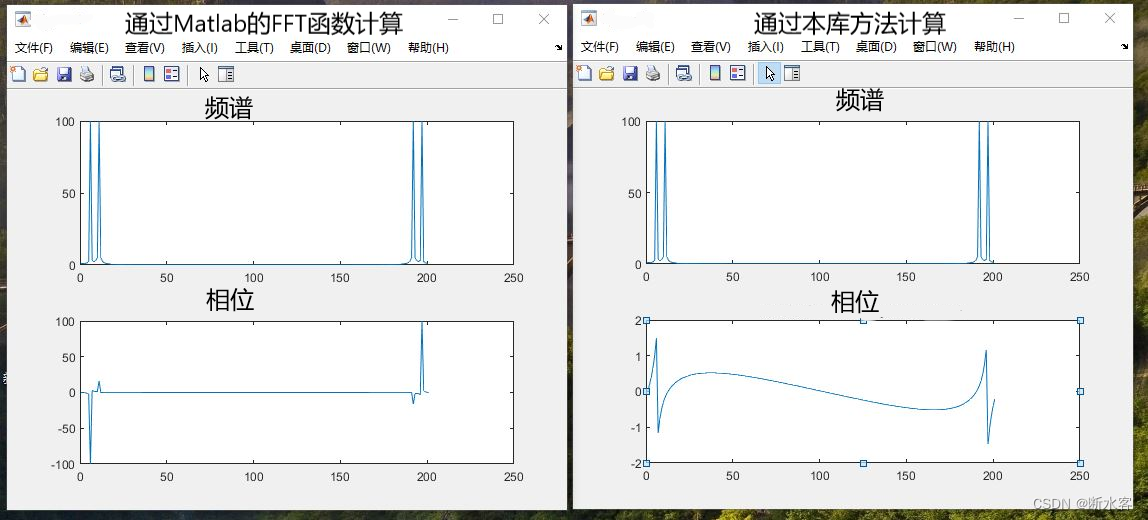
左边是用Matlab的FFT工具计算结果绘制的频谱，右图是用本文的函数得到的结果绘制的频谱。

4 结语

这里放出源码的Gitee仓库链接，自建工程编译运行后使用Matlab plot等绘图工具就可以得到文中地结果。

由于是C语言编写的，您也可以很方便地移植到单片机等嵌入式平台上。

遗憾的是，本文的傅里叶变换仅是没有采用蝴蝶算法的DFT，并不是快速傅里叶变换（DFT），后续对此将进行优化。

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系