高度平衡二叉搜索树
1. insert
一、先按照搜索树的规则找到插入点
二、插入数据
三、此时的树会发生变化
但是：
（1）在没有插入这个节点的时候，这个树还是高度平衡的，也就是说这个树的所有节点的平衡因子都是0或者1
（2）因为这个节点的插入，这个节点的所有父节点都会发生变化，我们按照规则将其（这些父节点的bf）重新赋值
1.curparent->left parent->bf–;
2.curparent->right parent->bf++:
3.更新以后，parent->bf0,更新结束。
说明：更新前parent->bf 是1或者-1，现在变成0，说明填上矮的那边，parent所在的子树高度不变
4.更新之后，parent->bf1/-1 继续往上更新。
说明：更新前，parent->bf 是0，现在变成1或者-1，我有一边变高了，parent所在的子树高度变了
5.更新以后，parent->bf==2/-2,parent所在子树已经不平衡了，需要旋转处理。
四、关于旋转处理
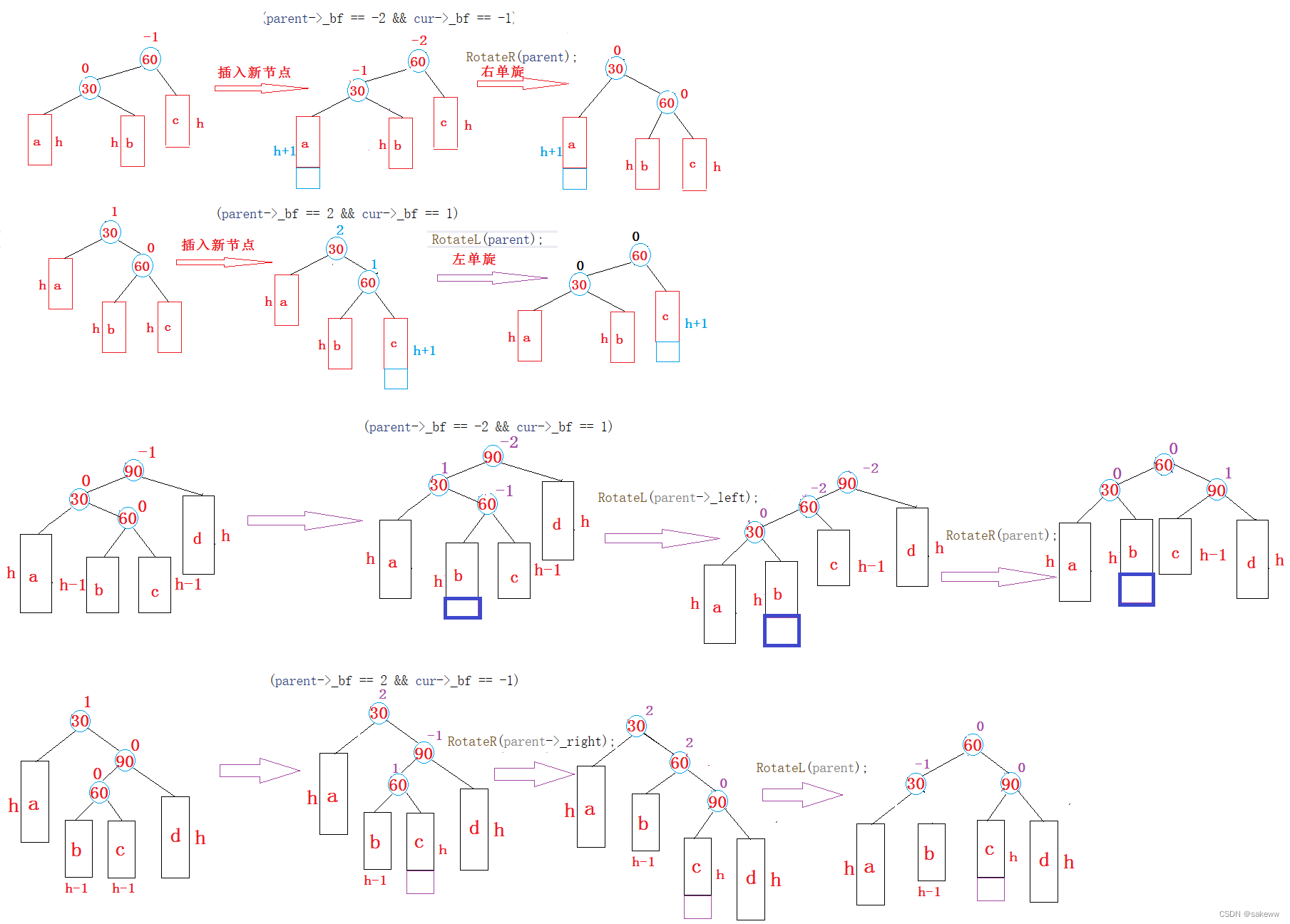
个人对这个旋转处理的理解：
- 一共四种情况，如果出现第五种情况，那么只能说明你的上一次旋转处理，处理的有问题，也就是你的代码写的有问题
- 比较难理解的是第一个和第三个
- 第一个
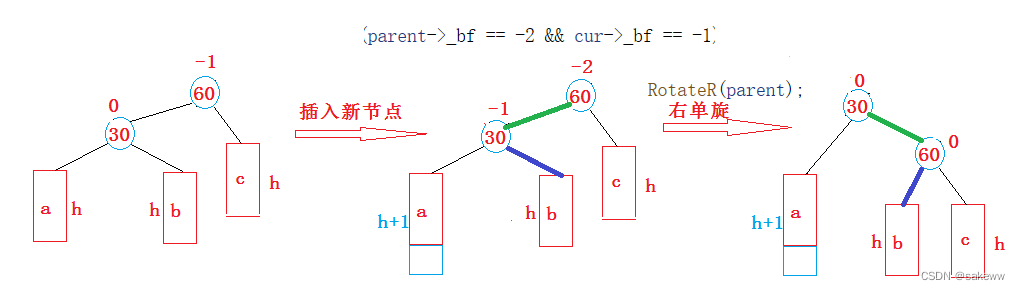需要变动的线，也就只有这两条，建议仔细观看这两条线段的变化，最好自己画一下，（不知道怎么说） - 第三个
需要变动的只是这三条线段，这三个线段的前世今生我也标记出来了
温馨提醒：这个代码有问题，但是整体思路是符合上述分析的那些点的
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while(cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else{
parent->_left = cur;
cur->_parent = parent;
}
//cur新增，只会影响cur祖先节点的平衡因子
//控制平衡
//1.更新平衡因子---新增节点到根节点的祖先路径
//2.出现异常的平衡因子，就需要旋转平衡处理
while (parent)
{
if (cur == parent->_left)
parent->_bf--;
else
parent->_bf++;
if (parent->_bf == 0)
break;
else if (parent->_bf == 1 || parent->_bf == -1)
{
//继续往上更新
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//旋转处理
if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == 1) // 左单旋
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
else
{
//说明插入更新平衡因子之前，树中的平衡因子就有问题了
assert(false);
}
}
return true;
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* parentParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (_root == parent){
_root = subR;
subR->_parent = nullptr;
}
else{
if (parentParent->_left == parent)
parentParent->_left = subR;
else
parentParent->_right = subR;
subR->_parent = parentParent;
}
subR->_bf = parent->_bf = 0;
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if(subLR) subLR->_parent = parent;//subLR可能为空
Node* parentparent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (parentparent->_left == parent)
parentparent->_left = subL;
else
parentparent->_right = subL;
subL->_parent = parentparent;
}
subL->_bf = 0;
parent->_bf = 0;
}
void RotateLR(Node* parent)
{
RotateL(parent->_left);
RotateR(parent);
}
void RotateRL(Node* parent)
{
RotateR(parent->_right);
RotateL(parent);
}
最终理解草图：
2. 如何判断你的AVL树符合规则
高度平衡
1.检查平衡因子？
不行，
因为平衡因子是你规定的，在你的代码中可能会直接设置的“正确”
2.检查高度？
int Height(Node* root)
{
if (root == nullptr) return 0;
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
return max(leftHeight, rightHeight)+1;
}
bool IsBalance()//balance均衡
{
return _IsBalance(_root);
}
bool _IsBalance(Node* root)
{
if (root == NULL) return true;
//对当前树进行检查
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
return abs(rightHeight - leftHeight) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
平衡因子是否正确
bool _IsBalance(Node* root)
{
if (root == NULL) return true;
//对当前树进行检查
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
if (rightHeight - leftHeight != root->_bf)
{
cout << root->_kv.first << "现在是:" << root->_bf << endl;
cout << root->_kv.first << "应该是:" << rightHeight - leftHeight << endl;
return false;
}
return abs(rightHeight - leftHeight) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
开始检查
当输入为：int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
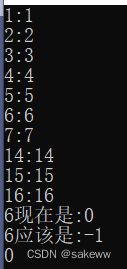
出现问题
解决步骤：
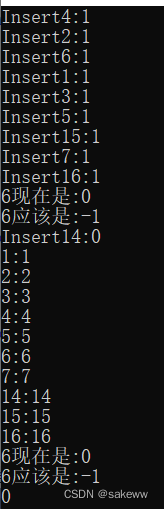
则可以推出是插入14时，出现问题
根据监控可以画出这个二叉树
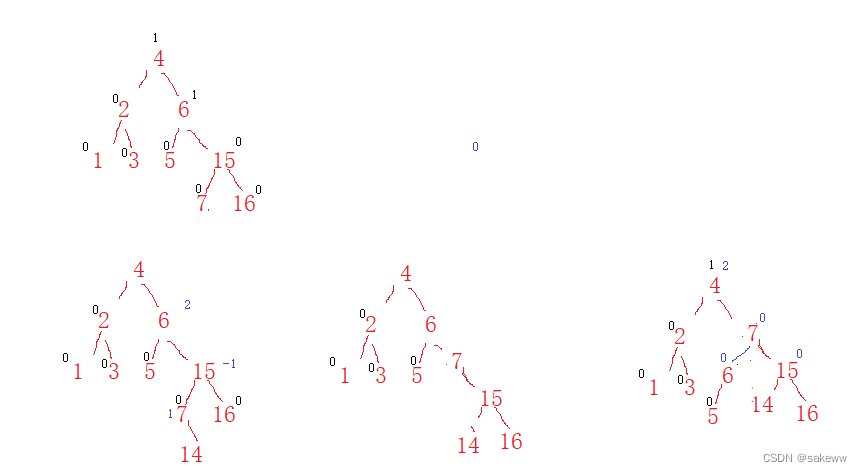
可以推出是双旋出了问题
双旋分为两种类型，各自三种情况
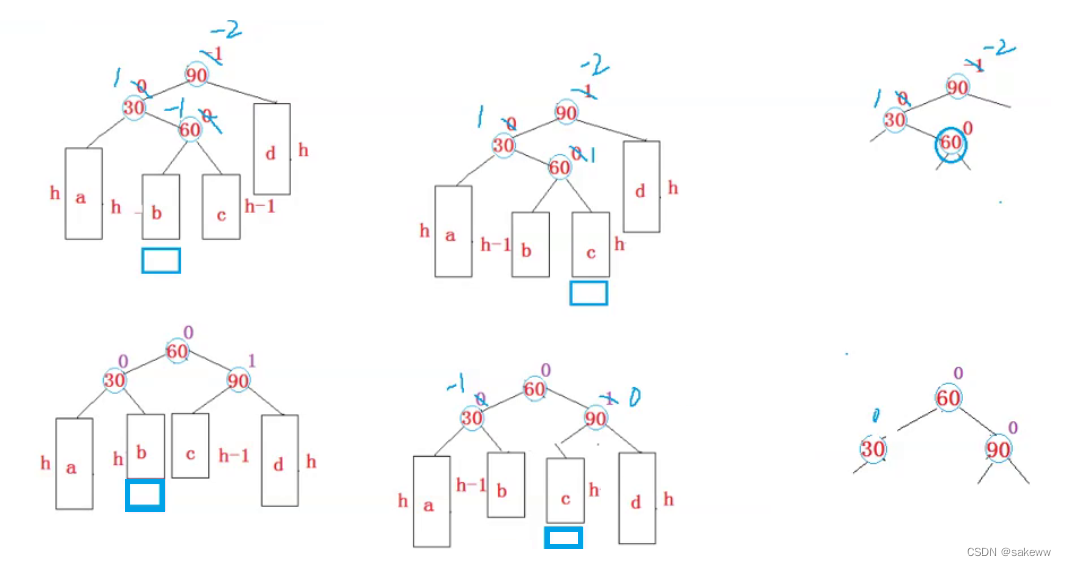
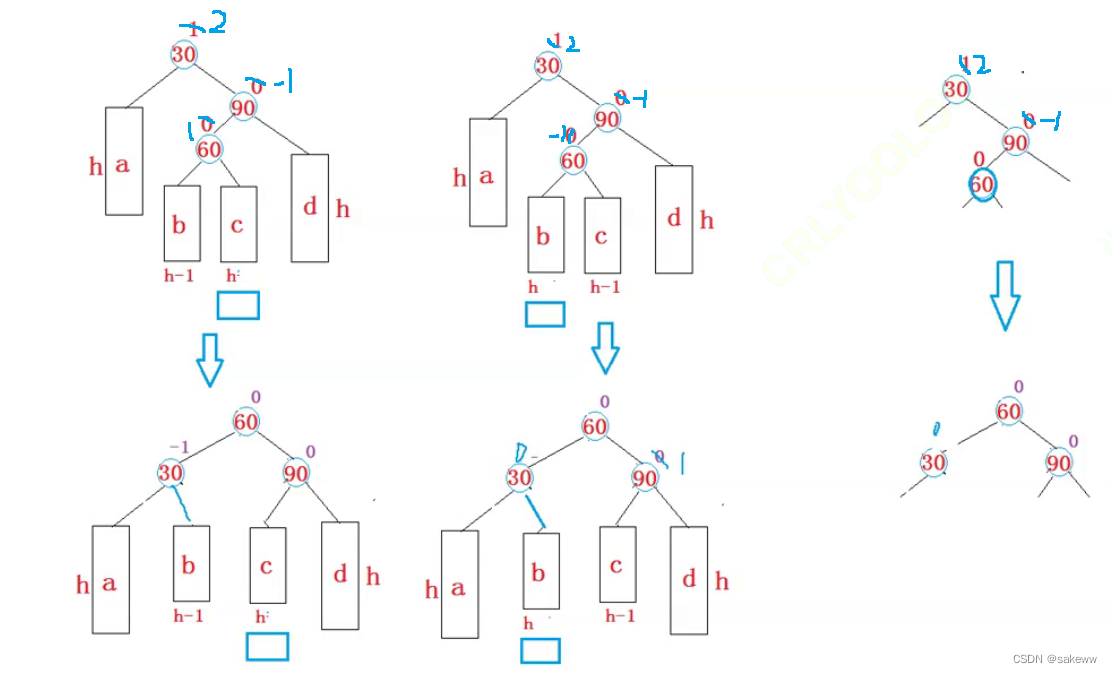
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 1)
{
parent->_bf = 0;
subR->_bf = -1;
subRL->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 1)
{
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
3.最终代码
#pragma once
template<class K,class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
pair<K, V> _kv;
int _bf;//balance factor 平衡因子
AVLTreeNode(const pair<K,V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_bf(0)
,_kv(kv)
{}
};
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
AVLTree()
:_root(nullptr)
{}
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while(cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else{
parent->_left = cur;
cur->_parent = parent;
}
//cur新增，只会影响cur祖先节点的平衡因子
//控制平衡
//1.更新平衡因子---新增节点到根节点的祖先路径
//2.出现异常的平衡因子，就需要旋转平衡处理
while (parent)
{
if (cur == parent->_left)
parent->_bf--;
else
parent->_bf++;
if (parent->_bf == 0)
break;
else if (parent->_bf == 1 || parent->_bf == -1)
{
//继续往上更新
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//旋转处理
if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == 1) // 左单旋
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
else
{
//说明插入更新平衡因子之前，树中的平衡因子就有问题了
assert(false);
}
}
return true;
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* parentParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (_root == parent){
_root = subR;
subR->_parent = nullptr;
}
else{
if (parentParent->_left == parent)
parentParent->_left = subR;
else
parentParent->_right = subR;
subR->_parent = parentParent;
}
subR->_bf = parent->_bf = 0;
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if(subLR) subLR->_parent = parent;//subLR可能为空
Node* parentparent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (parentparent->_left == parent)
parentparent->_left = subL;
else
parentparent->_right = subL;
subL->_parent = parentparent;
}
subL->_bf = 0;
parent->_bf = 0;
}
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 1)
{
parent->_bf = 0;
subR->_bf = -1;
subRL->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 1)
{
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
void InOder()
{
_InOrder(_root);
}
void _InOrder(Node* root)
{
if (root == NULL) return;
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
int Height(Node* root)
{
if (root == nullptr) return 0;
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
return max(leftHeight, rightHeight)+1;
}
bool IsBalance()//balance均衡
{
return _IsBalance(_root);
}
bool _IsBalance(Node* root)
{
if (root == NULL)
return true;
// 对当前树进行检查
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
if (rightHeight - leftHeight != root->_bf)
{
cout << root->_kv.first << "现在是:" << root->_bf << endl;
cout << root->_kv.first << "应该是:" << rightHeight - leftHeight << endl;
return false;
}
return abs(rightHeight - leftHeight) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
private:
Node* _root;
};
void TestAVLTree()
{
AVLTree<int, int> t;
int a[] = {4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
for (auto e : a)
{
t.Insert(make_pair(e, e));
cout << t.IsBalance() << endl;//检查代码
}
t.InOder();
cout << t.IsBalance() << endl;
}
