IEEE754浮点数

一个浮点数包括三部分: 符号部分(Sign)、指数部分(Exponent)、分数部分(Fraction)
- IEEE754浮点数不是均匀分布的。仅能代表有限个数的实数
- 对于normal浮点数,1.xxxx中的1是隐含存在的
- normal浮点数0有正负之分(S=0/1, E=0, Fraction=0)
- 有subnormal数(非常小,接近数值0): E=0, Fraction部分不为0
- IEEE754浮点数内部计算寄存器多出两位(保证gaurd & rounding)
- 有四种截断/舍入模式(rounding)
- 有overflow/underflow浮点计算异常。underflow危害不大,overflow需要特殊关注。overflow一个情形是从其他类型转换引起的(e.g.,一个很大的整数转成float, 或double转成float), 另外一个教科书级例子是hypot计算 x 2 + y 2 \sqrt{x^2+y^2} x2+y2?, 和求多维向量长度 ∑ x i 2 \sqrt{\sum{x_i^2}} ∑xi2??, 类似计算要时刻避免浮点overflow溢出!
- 比较: inf>1, 返回1; NaN>1、NaN==1、NaN<1都返回0
- 对于subnormal数一般有两种处理方式: flush to zero .vs. gradual underflow。subnormal数对性能影响较大,可以指定编译选项打开或关闭lush to zero;gradual underflow一般对比较精细计算中有帮助,比如求函数数值导数等。
单精度浮点数可表示范围:
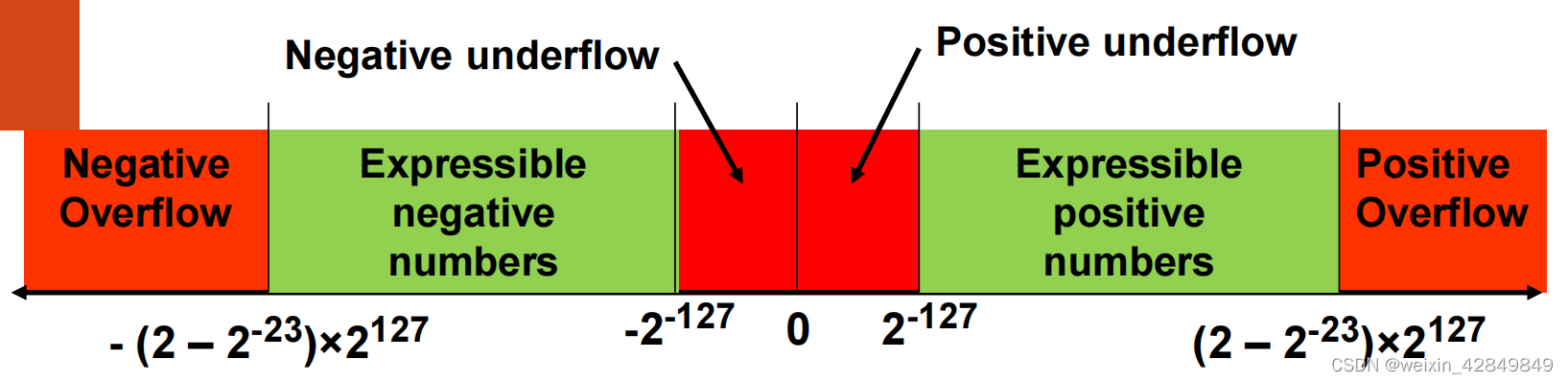
单精度(float,32bits)
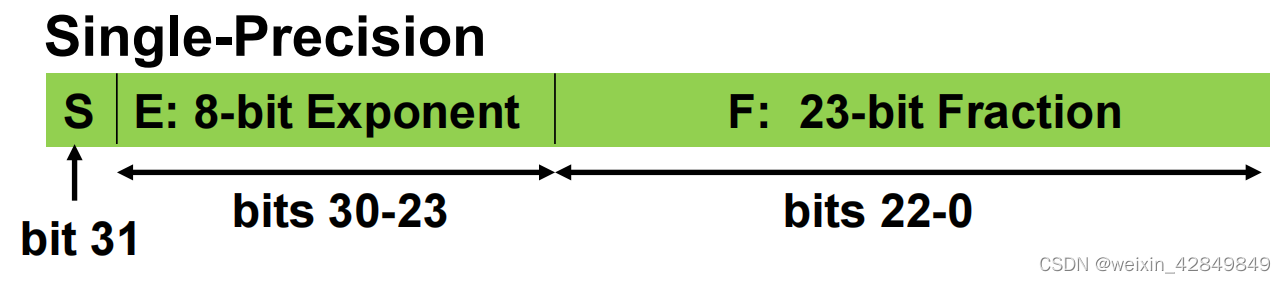
| 说明 | |
|---|---|
| Bias | 127 |
| E范围 | [1…254], 0和255保留 |
| Range | 2 ? 126 2^{-126} 2?126 to 2 + 127 2^{+127} 2+127 |
一些特殊单精度数(调用std::numeric_limits<float>获取)
| 浮点数 | 二进制表示 |
|---|---|
| 0 | 00000000000000000000000000000000 |
| -0 | 10000000000000000000000000000000 |
| 1 | 00111111100000000000000000000000 |
| -1 | 10111111100000000000000000000000 |
| eps | 00110100000000000000000000000000 |
| 1+eps | 00111111100000000000000000000001 |
| min | 00000000100000000000000000000000 |
| max | 01111111011111111111111111111111 |
| denorm_min | 00000000000000000000000000000001 |
| infinity | 01111111100000000000000000000000 |
| sNaN | 01111111101000000000000000000000 |
| qNaN | 01111111110000000000000000000000 |
双精度(double,64bits)
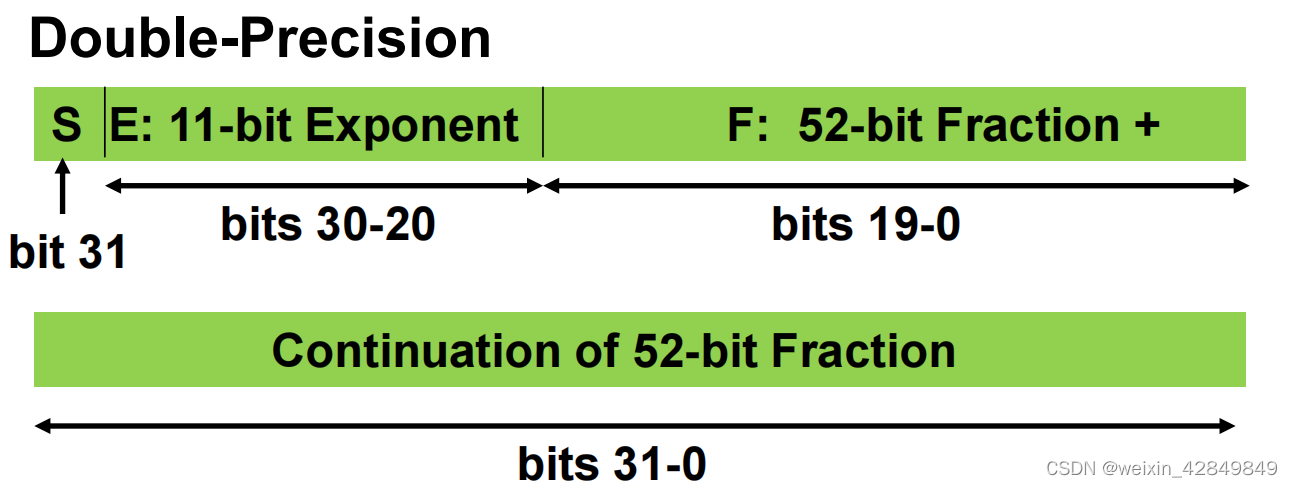
| 说明 | |
|---|---|
| Bias | 1023 |
| E范围 | [1…2046], 0和2047保留 |
| Range | 2 ? 1022 2^{-1022} 2?1022 to 2 + 1023 2^{+1023} 2+1023 |
一些特殊双精度数(调用std::numeric_limits<double>获取)
| 浮点数 | 二进制表示 |
|---|---|
| 0 | 0000000000000000000000000000000000000000000000000000000000000000 |
| -0 | 1000000000000000000000000000000000000000000000000000000000000000 |
| 1 | 0011111111110000000000000000000000000000000000000000000000000000 |
| -1 | 1011111111110000000000000000000000000000000000000000000000000000 |
| eps | 0011110010110000000000000000000000000000000000000000000000000000 |
| 1+eps | 0011111111110000000000000000000000000000000000000000000000000001 |
| min | 0000000000010000000000000000000000000000000000000000000000000000 |
| max | 0111111111101111111111111111111111111111111111111111111111111111 |
| infinity | 0111111111110000000000000000000000000000000000000000000000000000 |
| sNaN | 0111111111110100000000000000000000000000000000000000000000000000 |
| qNaN | 0111111111111000000000000000000000000000000000000000000000000000 |
浮点数加减法流程逻辑

工具程序
/************************************
测试IEEE浮点数标准、表示形式等
*************************************/
#include <cmath>
#include <iostream>
#include <bitset>
#include <limits>
#include <type_traits>
#include <cstdint>
#include <sstream>
#include <string>
using namespace std;
template<typename R>
std::ostream &dump_bits(const R x,std::ostream &os=std::cout)
{
uint8_t *u8=(uint8_t *)&x;
string s("");
//assume little-endian
for(int i=sizeof(R)-1; i>=0; --i)
{
std::bitset<8> b(u8[i]);
s+=b.to_string();
}
os<<s;
return os;
}
template<typename R>
std::ostream &dump_hex(const R x,std::ostream &os=std::cout)
{
os<<std::hexfloat;
os<<x;
os<<std::defaultfloat;
return os;
}
template<typename T>
void print_limits()
{
using flimits=numeric_limits<T>;
cout<<"radix:\t"<<flimits::radix<<"\n";
cout<<"min_exponent:\t"<<flimits::min_exponent<<"\n";
cout<<"max_exponent:\t"<<flimits::max_exponent<<"\n";
cout<<"digits:\t"<<flimits::digits<<"\n";
cout<<"digits10:\t"<<flimits::digits10<<"\n";
cout<<"epsilon:\t"<<flimits::epsilon()<<"\n";
cout<<"inf:\t"<<flimits::infinity()<<"\n";
cout<<"qNan:\t"<<flimits::quiet_NaN()<<"\n";
cout<<"sNan:\t"<<flimits::signaling_NaN()<<"\n";
cout<<"min:\t"<<flimits::min()<<"\n";
cout<<"max:\t"<<flimits::max()<<"\n";
}
template<typename T>
void print_bits_and_hex()
{
static_assert(std::is_same_v<T,float> || std::is_same_v<T,double> || std::is_same_v<T,long double>);
using flimits=numeric_limits<T>;
auto dump=[](std::ostream &os, string name, const T &x)->std::ostream &
{
os<<name<<"\t";
dump_bits(x,os);
os<<" ";
os<<std::hexfloat;
os<<x;
os<<std::defaultfloat;
os<<"\n";
return os;
};
dump(cout,"infinity",flimits::infinity());
dump(cout,"sNaN",flimits::signaling_NaN());
dump(cout,"qNaN",flimits::quiet_NaN());
dump(cout,"0",T(0.0));
dump(cout,"-0",T(-0.0));
dump(cout,"1",T(1));
dump(cout,"-1",T(-1));
dump(cout,"eps", flimits::epsilon());
dump(cout,"1+eps", flimits::epsilon()+T(1));
dump(cout,"min",flimits::min());
dump(cout,"max",flimits::max());
dump(cout,"denorm_min",flimits::denorm_min());
}
int main(int argc, char **argv)
{
cout<<R"(
=========================================================================
单精度浮点数(float) limits
=========================================================================)"<<"\n";
print_limits<float>();
cout<<R"(
=========================================================================
双精度浮点数(double) limits
=========================================================================)"<<"\n";
print_limits<double>();
cout<<R"(
=========================================================================
单精度浮点数(float)二进制模式
=========================================================================)"<<"\n";
print_bits_and_hex<float>();
cout<<R"(
==========================================================================
双精度浮点数(double)二进制模式
==========================================================================)"<<"\n";
print_bits_and_hex<double>();
cout<<R"(
==========================================================================
长精度浮点数(long double)二进制模式
==========================================================================)"<<"\n";
print_bits_and_hex<long double>();
//=======================================================================
//inf可和其他结果比较
cout<<((numeric_limits<float>::infinity()>1.0f)?"inf>1":"inf<=1")<<"\n";
//inf参加运算,结果是inf
cout<<numeric_limits<float>::infinity()/2.0f<<"\n";
//nan和其他数值比较,结果都为false
cout<<(numeric_limits<float>::quiet_NaN()>1.0f)<<"\n";
cout<<(numeric_limits<float>::quiet_NaN()<1.0f)<<"\n";
//0有特殊运算定义
cout<<(-0.0f<0.0f)<<"\n";
return(0);
}
//编译: g++ -std=c++17 cxx_ex3.cpp