二叉搜索树的特征
- 左子树永远比根节点小,右子树永远比根节点大
- 也是key模型,看某个数据在不在集合里面。
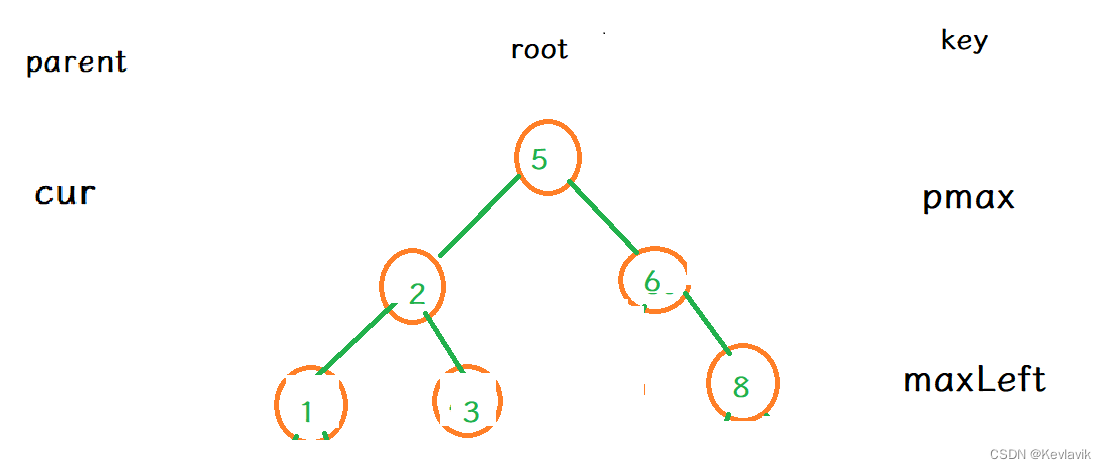
搜索树的添加
- key值比根值大,往右边插入,小,往左边插入
- key值和根节点值比较,确定插入在根节点的左边还是右边,根节点一定是某个叶子结点。
- 比如插入 4,一定是在3的右边
- 下面的x 当作key
template<class K>
struct bstn
{
bstn()
{
cout << "单个链表结点的声明初始化" << endl;
}
bstn(const K& x)
:_left(nullptr)
, _right(nullptr)
, _value(x)
{
}
bstn* _left;
bstn* _right;
K _value;
};
template<class K>
bool bst<K>::Insert(const K& x)
{
return bst<K>::_Insert(x);
}
template<class K>
bool bst<K>::_Insert(const K& x)
{
if (_root==nullptr)/ /空树的处理
{
_root = new Node(x);/ /调用自定义类型并用x初始化
return true;
}
Node* parent = nullptr;/ /防止走到空找不到根节点
Node* cur = _root;
while (cur)
{
/ /比右边大,就去右子树的右边插入,
if (x>cur->_value)
{
parent = cur;
cur = cur->_right;
}
else if(x<cur->_value) / /,比根值 小去左边插入
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
/ /这个版本的搜索二叉树不支持值相等
}
}
/ /一定比叶子节点值 大或小 进行连接插入
cur = new Node(x); /new会调用自定义类型的构造函数初始化
if (parent->_value < cur->_value) /判断插入在根的左边还是右边
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
搜索树的遍历打印
template<class K>
bool bst<K>::Ergodic()
{
return _Ergodic(_root);
}
template<class K>
bool bst<K>::_Ergodic(Node* root)
{
/视为一个满二叉树进行遍历,找到我左为空返回,根,右子树为空返回,在返回上一层;以此类推
if (root == nullptr)
{
return false;
}
_Ergodic(root->_left);
cout << root->_value << " ";
_Ergodic(root->_right);
}
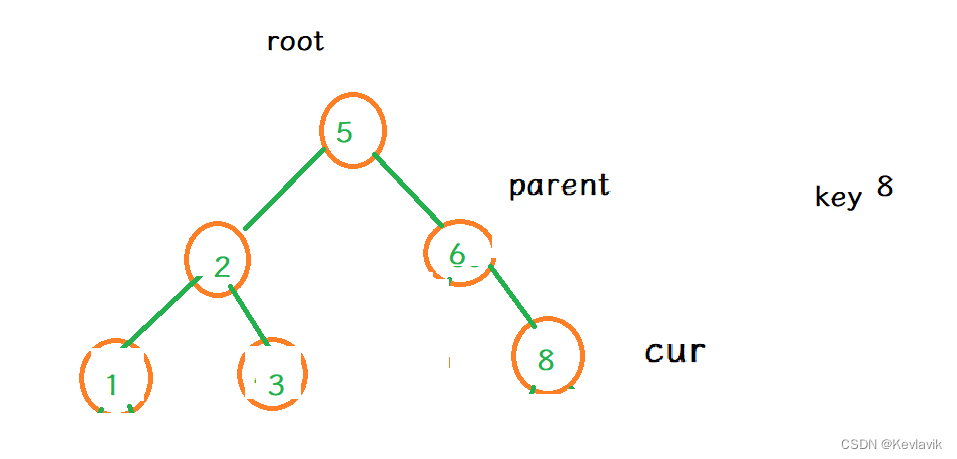
搜索树的查找
- key值比根值大,往右边找;比根值小,往左边找,比如说找:8
Node* FindR(const K& key)
{
return _FindR(_root, key);
}
Node* _Find(const K& x)
{
Node* cur = _root;
while (cur)
{
if (x>cur->_value)
{
cur = cur->_right;
}
else if(x<cur->_value)
{
cur = cur->_left;
}
else
{
/ /不小于左边,不大于右边
return cur;
}
}
return nullptr;
}
搜索二叉树的删除
- 先找到那个值:key值比根值大,往右边找;比根值小,往左边找,
- 找到以后两种情况:
- (key值)结点的一侧为空 ,父结点连接上不为空的一侧,删除(key值)结点;5,6,8.删除5
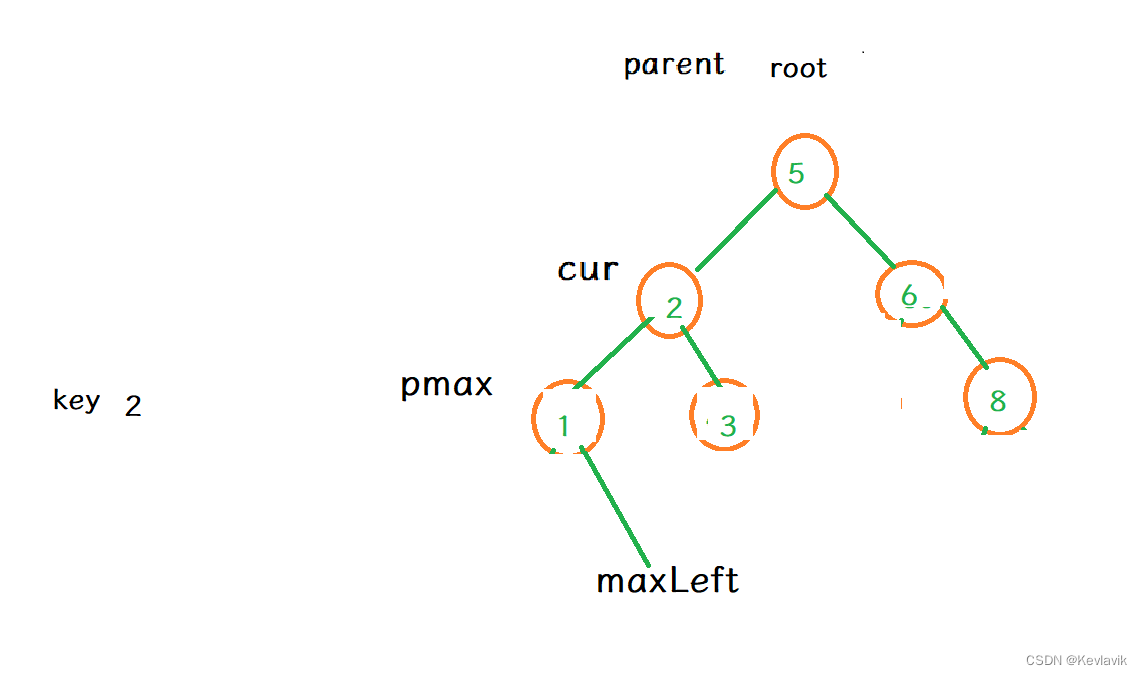
- (key值)结点的两侧都不为空:找(key值)左右两边的最值替换:找左边最大的或右边最小的替换。
- 往根的左边走一步,如果右边不为空,然后持续往右走;最大值的右子树必然是空,往右找到空,记录父节点,然后删除最大值节点。
- 比如删除 2
bool Erase(const K& key)
{
return _Erase(_root, key);
}
template<class K>
bool bst<K>::_Erase(const K& x) / /x ---》 key
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_value < x)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_value>x)
{
parent = cur;
cur = cur->_left;
}
else / /上面走完之后 此处 值相等 找到
{
/ /左子树或右子树为空,双亲结点连接上孩子结点不为空的一侧,删除key值节点
if (cur->_left == nullptr)
{
if (_root == cur)
{
_root = cur->_right;
}
else
{
if (cur = parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (_root == cur)
{
_root = cur->_left;
}
else
{
if (cur = parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else / /两边都不为空 左边的最大值节点和 key节点交换值 , 删除最大值节点
{
Node* maxLeft = cur->_left;
Node* pmax = cur;
while (maxLeft->_right) / /不为空就往右边走 一个值记录最值的父节点
{
pmax = maxLeft;
maxLeft = maxLeft->_right;
}
cur->_value = maxLeft->_value;
if (pmax->_right=maxLeft) / /此时最大值节点的右边为空,左边还可能有子树比它小的
{
pmax->_right = maxLeft->_left;/ / 判断最大值节点是父结点的哪一边
}
else / /让父节点接上最大值节点的左子树
{
pmax->_left = maxLeft->_left;
}
delete maxLeft;
}
return true; / /删除完成返回
}
}
return false; / /走到空说明没有那个值
}
递归版本
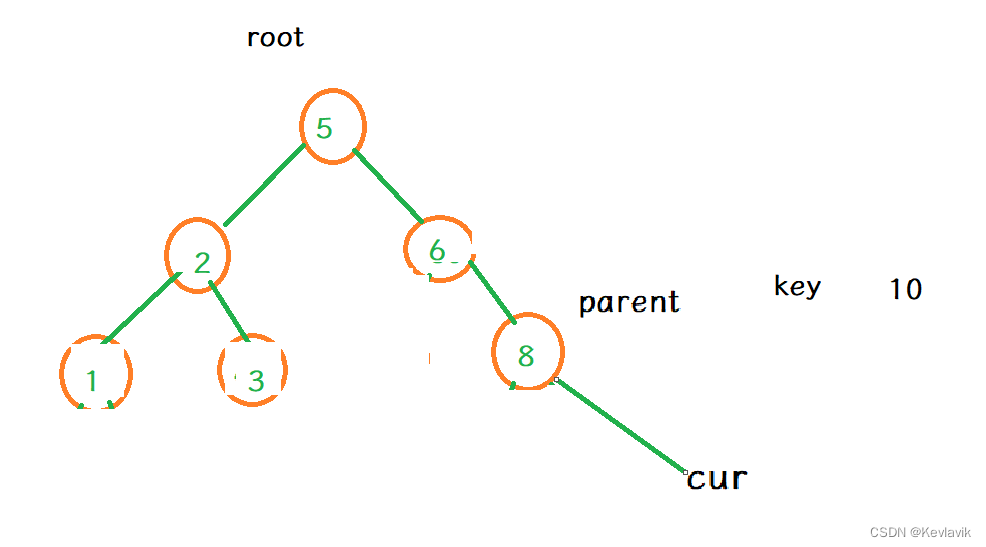
递归插入
- 插入10
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
template<class K>
bool bst<K>::_InsertR(Node*& root, const K& key)
{
if (root==nullptr) / /是对8右指针的引用
{
root = new Node(key); / / 8->right = .....接上即可
return true;
}
else
{
if (root->_value < key)
return _InsertR(root->_right, key);
else if (root->_value > key)
return _InsertR(root->_left, key);
else
return false;
}
}
递归查找
- 比如查找:3
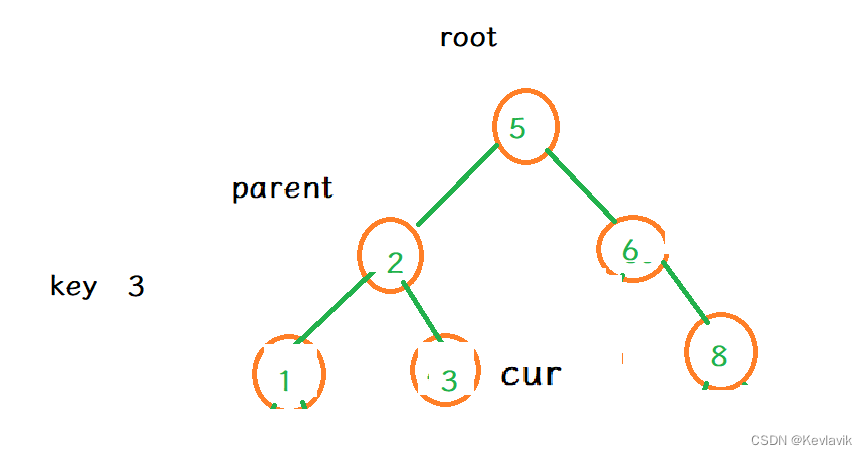
Node* FindR(const K& key)
{
return _FindR(_root, key);
}
template<class K>
bst<K>::Node* bst<K>::_FindR(Node*& root,const K& key) / /3
{
if (root == nullptr) / /2的右子树引用 3
{
return nullptr;
}
if (root->_value < key) / /2
return _FindR(root->_right, key); / /不大
else if (root->_value > key) / / 5 2 / /不小
return _FindR(root->_left, key);
else
return root; / /相等返回 秒啊
}
递归删除
- 比如删除:2
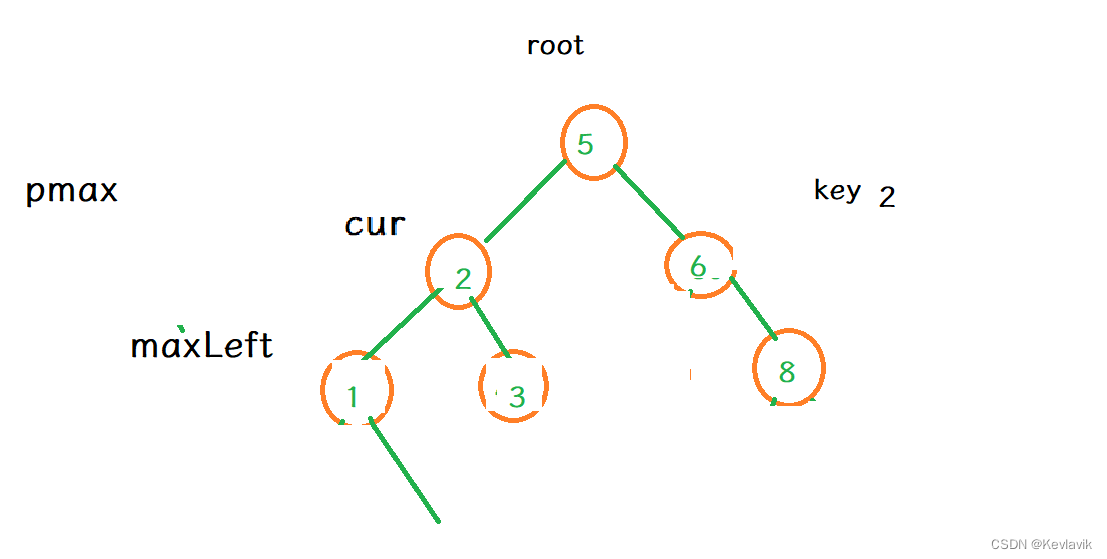
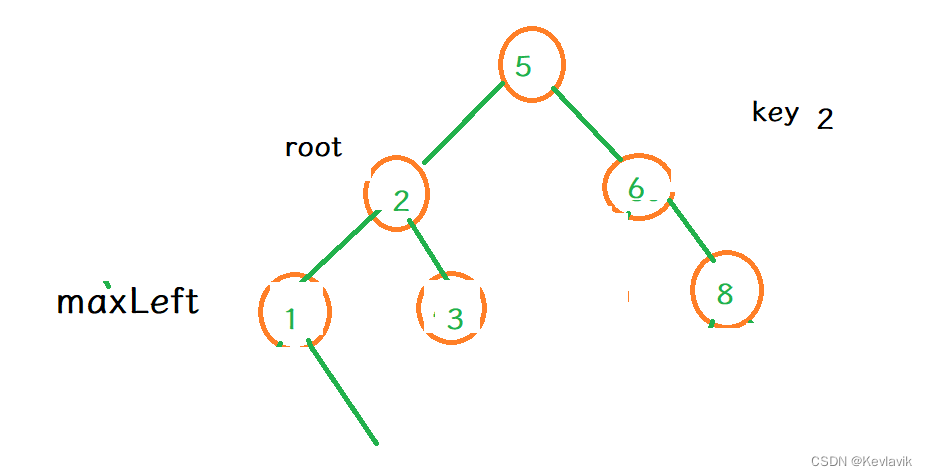
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
template<class K>
bool bst<K>::_EraseR(Node*& root,const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_value<key)
{
return _EraseR(root->_right, key);
}
else if (root->_value>key) / /5 > 2
{
return _EraseR(root->_left, key); / /ture 返回....
}
else
{
Node* del = root; / /root 是 对2的引用 也是2这个节点
if (root->_left == nullptr)
{
root == root->_right;/ / 5的left 链接到key值不为空的一侧
}
else if (root->_right == nullptr)
{
root = root->_left; / /最后删除del
}
else / / 有 1 3
{
Node* maxLeft = root->_left; / /root 还是2
while (maxLeft->_right) / / 左孩子节点的右子树为空则 说明左孩子的值就是最大值
{
maxLeft = maxLeft->_right;
}
root->_value = maxLeft->_value;/ /替换
return _Erase(root->_left,maxLeft->key); / /再递归删除 最大值节点
/ / 2的左边引用 1 相等 ; 1的节点交给 del ;1的左边为空, 2左边的引用 链接到引用的右边;删除 del ,返回。
}
delete del;
return true;
}
}
接口总览
template<class K>
class bst
{
public:
typedef bstn<K> Node;
bst()
{
cout << "搜索二叉树的节点" << endl;
}
bool Insert(const K& x);
bool Ergodic();
Node* Find(const K& x)
{
return _Find(x);
}
bool Erase(const K& x)
{
return _Erase(x);
}
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
Node* FindR(const K& key)
{
return _FindR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
bool _Insert(const K& x);/ /隐藏实现细节
bool _Ergodic(Node* root);
bool _Erase(const K& x);
Node* _Find(const K& x)
{
Node* cur = _root;
while (cur)
{
if (x>cur->_value)
{
cur = cur->_right;
}
else if(x<cur->_value)
{
cur = cur->_left;
}
else
{
/ /不小于左边,不大于右边
return cur;
}
}
return nullptr;
}
bool _InsertR(Node*& root,const K& key);
Node* _FindR(Node*& root,const K& key);
bool _EraseR(Node*& root,const K& key);
Node* _root;
};
key-Value 模型
- 场景:字典翻译,统计单词出现的次数; 刷身份证进站。
- 是对Key模型的改造:
- 添加一个V模板参数即可,添加时多添加一个参数
- 找到Key就能删除Value
基建
namespace KEY_VALUE
{
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
: _left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
.....
private:
Node* _root = nullptr;
}
key-Value的添加
bool _InsertR(Node*& root, const K& key, const V& value)
{
if (root==nullptr)
{
root = new Node(key,value);
return true;
}
else
{
if (root->_key < key)
return _InsertR(root->_right, key);
else if (root->_key > key)
return _InsertR(root->_left, key);
else
return false;
}
}
key-Value的遍历打印
bool _Ergodic(Node* root)
{
if (root == nullptr)
{
return false;
}
_Ergodic(root->_left);
cout << root->_key << " "<<root->_value<<endl;
_Ergodic(root->_right);
}
key-Value的查找
Node* _FindR(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key>cur->_key)
{
cur = cur->_right;
}
else if(key<cur->_key)
{
cur = cur->_left;
}
else
{
/ /不小于左边,不大于右边
return cur;
}
}
return nullptr;
}
key-Value的删除
bool _EraseR(Node*& root,const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key<key)
{
return _EraseR(root->_right, key);
}
else if (root->_key>key)
{
return _EraseR(root->_left, key);
}
else
{
Node* del = root;
if (root->_left == nullptr)
{
root == root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* maxLeft = root->_left;
while (maxLeft->_right)
{
maxLeft = maxLeft->_right;
}
root->_key = maxLeft->_key;/ /替换
root->_value =maxLeft->_value;
return _Erase(root->_left,maxLeft->_key); / /再递归删除 最大值节点
}
delete del;
return true;
}
}
简单字典
void TestDict()
{
KEY_VALUE::BSTree<string, string> dict;
dict.InsertR("crash", "崩溃");
dict.InsertR("priority", "优先级");
string str;
while (cin >> str)
{
if (str == "Q")/ /quit 退出
{
break;
}
else
{
auto ret = dict.FindR(str); / /返回的是个结构体指针Node*
if (ret == nullptr)
{
cout << "This word is not available in the dictionary, please re-enter it" << endl;
}
else
{
cout << ret->_key << "->" << ret->_value << endl;
}
}
}
}
统计单词(字符串)出现次数
void TestCWord()
{
string str[] = { "i","dont","have","a","dream","when","i","was","a","child" };
KEY_VALUE::BSTree<string, int> countree;
for (auto& i : str)
{
auto ret = countree._FindR(i);
if (ret==nullptr)
{
countree._InsertR(i, 1);/ /没有则进行插入,次数是第一次
}
else
{
ret->_value++;/ /有则 int value ++
}
}
countree._Ergodic();
}
结束
- 按时吃饭,不要熬夜,太累了就睡觉…

| 






