参考文献:Malkin Z. A new method to subdivide a spherical surface into equal-area cells[J]. arXiv preprint arXiv:1612.03467, 2016.
一种根据面积均分球面的方法是根据经纬度来分,即将直角坐标
(
x
,
y
,
z
)
(x,y,z)
(x,y,z)转换成极坐标
(
θ
,
?
,
r
)
(\theta, \phi, r)
(θ,?,r),然后将
θ
\theta
θ和
?
\phi
?均分。均分
?
\phi
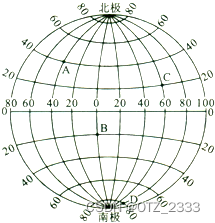
?(经度)确实能让分出来的小块面积相等,但
θ
\theta
θ(维度)分块后是不均匀的,如下图
网上找到一篇博客介绍了两种均分方法:正多面体(柏拉图体regular polyhedron)、Hierarchical Equal Area isoLatitude Pixelization(这个方法甚至专门有个c++库)

但是这两种方法感觉在原理和实现上都很复杂,于是经过一番搜寻找到了论文16年的一篇论文《A new method to subdivide a spherical surface into equal-area cells》
方法
这篇论文的方法跟开头介绍的错误分法都是从经纬度( θ \theta θ和 ? \phi ?)下手,但它并不是均分。主要步骤分两步:
- 首先将纬度划分成
x
x
x块
- 相邻块之间的宽度不完全一样,但是大致相同,而且整个划分关于赤道对称
- 将每一个纬度带
i
(
i
=
1
,
2
,
.
.
.
,
x
)
i(i=1,2,...,x)
i(i=1,2,...,x),均分成
y
i
y_i
yi?块。
- 不同纬度带划分的块数不一样。纬度越高块数越少,赤道附近的块接近正方形
- 同样关于赤道对称
- 要求划分完成后每一块的面积相等
划分的方法论文中并没有给,只给了将球面均分成46、130、406块的划分方式
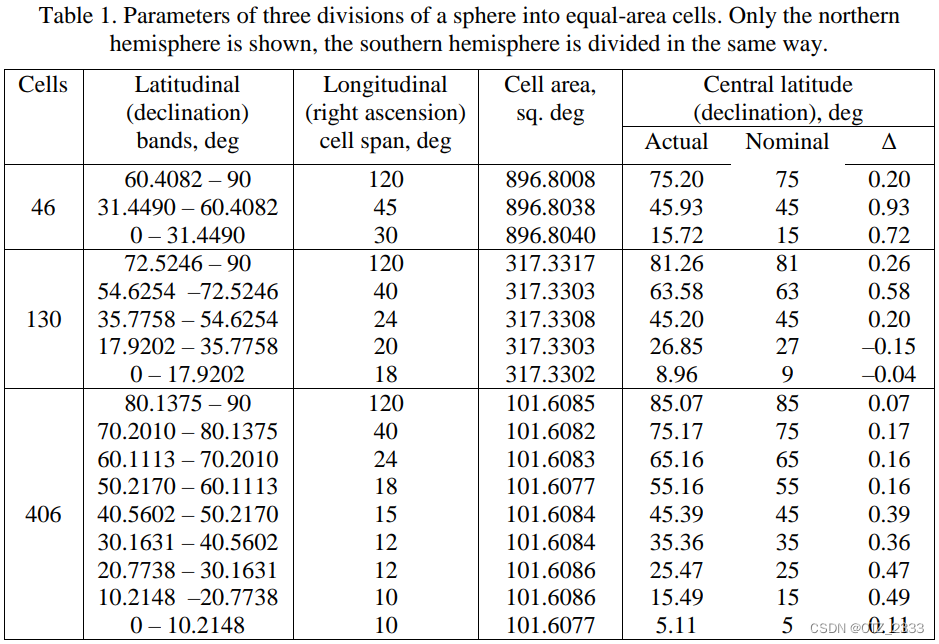
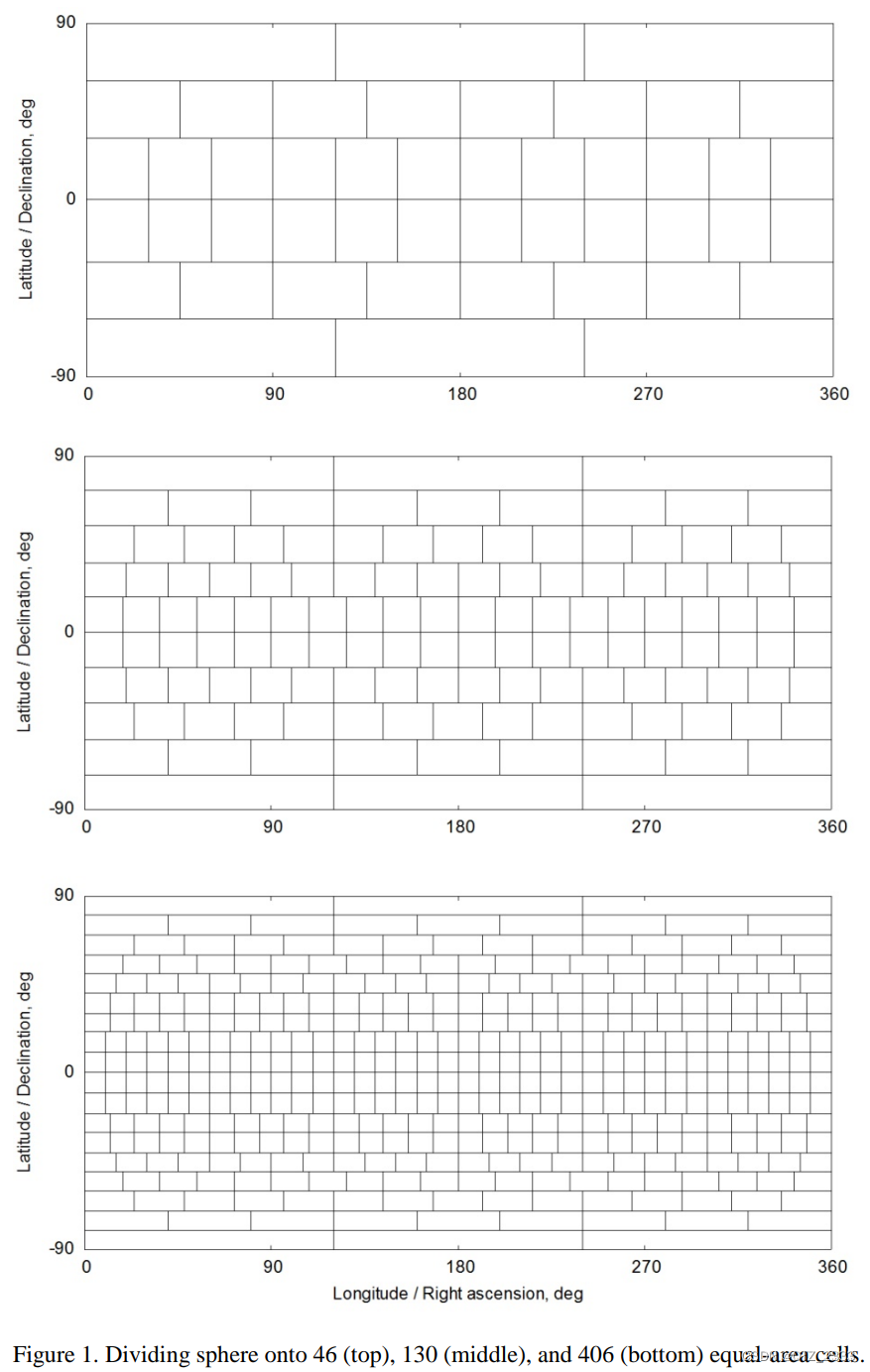
由于我手边工作的需要,这些划分数量太多了,我就自己手推了
x
=
4
x=4
x=4和
x
=
5
x=5
x=5的划分方式,而且我并没有要求“赤道附近的块接近正方形”
x = 4 x=4 x=4的划分方式
- 因为关于赤道对称,上半球有两个纬度带,最高纬度带对应角度为 θ \theta θ,第二个为 π / 2 ? θ \pi/2-\theta π/2?θ
- 最高纬度带的面积可以用球冠面积公式得到
S 1 = 2 π r h = 2 π r ( 1 ? c o s θ ) r = 2 π r 2 ( 1 ? c o s θ ) S_1=2\pi rh=2\pi r (1-cos\theta)r=2\pi r^2 (1-cos\theta) S1?=2πrh=2πr(1?cosθ)r=2πr2(1?cosθ) - 根据半球面积可以计算得到第二个纬度带的面积
S 2 = S 半 球 ? S 1 = 2 π r 2 ? 2 π r 2 ( 1 ? c o s θ ) = 2 π r 2 c o s θ S_2 = S_{半球}-S_1 = 2\pi r^2 - 2\pi r^2 (1-cos\theta) =2 \pi r^2 cos\theta S2?=S半球??S1?=2πr2?2πr2(1?cosθ)=2πr2cosθ - 假设第一个纬度带分
m
m
m块,第二个纬度带分
n
n
n块,则要求
2 π r 2 ( 1 ? c o s θ ) m = 2 π r 2 c o s θ n ( 1 ? c o s θ ) c o s θ = m n \frac{2\pi r^2 (1-cos\theta)}{m}=\frac{2\pi r^2 cos\theta }{n}\\ \frac{(1-cos\theta)}{cos\theta }=\frac{m}{n} m2πr2(1?cosθ)?=n2πr2cosθ?cosθ(1?cosθ)?=nm? - (可选)如果想要让赤道附近的块尽量接近正方形,我们可以大致估算一下
n
n
n的范围
- 赤道附近的每个块的高度(纬度带的宽度)为 h = r ? ( π / 2 ? θ ) h=r*(\pi/2-\theta) h=r?(π/2?θ)
- 赤道附近的纬度带分
n
n
n块,则我们想要上下边的长度尽量接近高度,即
l 上 = 2 π r s i n θ n ≈ r ? ( π / 2 ? θ ) → n = 2 π s i n θ π / 2 ? θ l 下 = 2 π r n ≈ r ? ( π / 2 ? θ ) → n = 2 π π / 2 ? θ l_{上}=\frac{2\pi r sin\theta}{n}\approx r*(\pi/2-\theta)\rightarrow n = \frac{2\pi sin\theta}{\pi/2-\theta}\\ l_{下}=\frac{2\pi r }{n} \approx r*(\pi/2-\theta)\rightarrow n = \frac{2\pi}{\pi/2-\theta} l上?=n2πrsinθ?≈r?(π/2?θ)→n=π/2?θ2πsinθ?l下?=n2πr?≈r?(π/2?θ)→n=π/2?θ2π? - 将这两条线画出来可以看到
n
n
n越大,越接近正方形
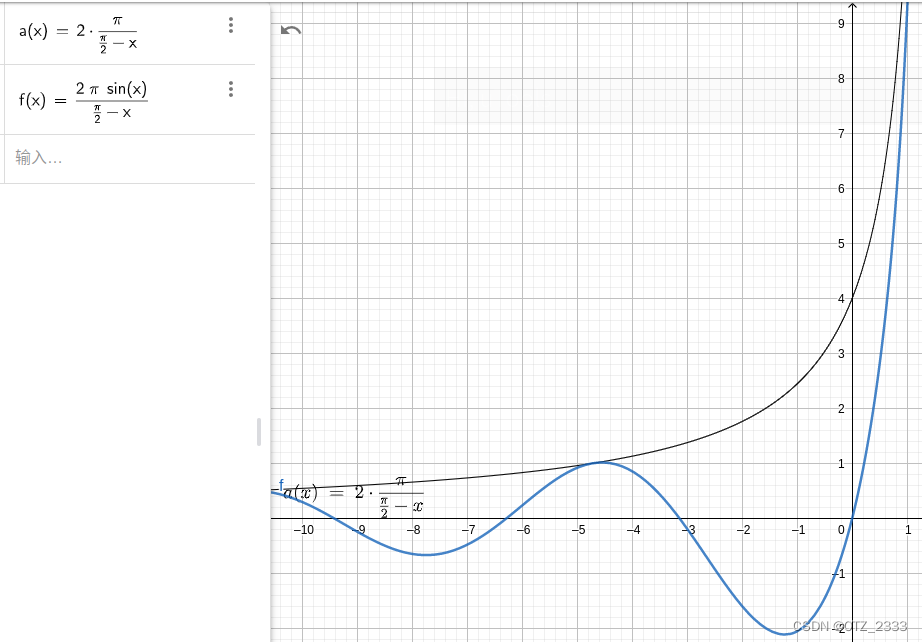
- (可选)如果想要纬度带宽度大致相同,即要求
θ
≈
π
/
4
\theta\approx\pi/4
θ≈π/4,带入之前的公式得
m n = ( 1 ? c o s θ ) c o s θ ≈ ( 1 ? c o s π / 4 ) c o s π / 4 ≈ 0.414 \frac{m}{n}=\frac{(1-cos\theta)}{cos\theta }\approx \frac{(1-cos\pi/4)}{cos\pi/4 }\approx0.414 nm?=cosθ(1?cosθ)?≈cosπ/4(1?cosπ/4)?≈0.414 - 接下来只要按照想要的划分方式给
m
m
m和
n
n
n赋整数,就能求解
θ
\theta
θ,例如
- m = 2 , n = 3 , θ = 53.130 ° m=2, n=3, \theta=53.130\degree m=2,n=3,θ=53.130°
- m = 3 , n = 4 , θ = 55.150 ° m=3, n=4, \theta=55.150\degree m=3,n=4,θ=55.150°
- m = 3 , n = 5 , θ = 51.318 ° m=3, n=5, \theta=51.318\degree m=3,n=5,θ=51.318°
- m = 4 , n = 5 , θ = 56.217 ° m=4, n=5, \theta=56.217\degree m=4,n=5,θ=56.217°
- m = 3 , n = 6 , θ = 48.190 ° m=3, n=6, \theta=48.190\degree m=3,n=6,θ=48.190°
- m = 3 , n = 7 , θ = 45.573 ° m=3, n=7, \theta=45.573\degree m=3,n=7,θ=45.573°
| Total Cell | Cells | Latitudinal | Longitudinal |
|---|---|---|---|
| 10 | 2 3 3 2 | 0-53.13° 53.13°-90° 90°-126.87° 126.87°-180° | 180° 120° 120° 180° |
| 14 | 3 4 4 3 | 0-55.15° 55.15°-90° 90°-124.85° 124.85°-180° | 120° 90° 90° 120° |
| 18 | 4 5 5 4 | 0-56.22° 56.22°-90° 90°-123.78° 123.78°-180° | 90° 72° 72° 90° |
| 20 | 3 7 7 3 | 0-45.573° / 0 - 0.7954 45.573°-90° / 0.7954 - 1.5708 90°-134.427° / 1.5708 - 2.3462 134.427°-180° / 2.3462 - 3.1416 | 120° / 2.0944 51.43° / 0.8976 51.43° / 0.8976 120° / 2.0944 |
x = 5 x=5 x=5的划分方式
- 虽然 x = 5 x=5 x=5为奇数,但是因为关于赤道对称,这里算上半球有2.5个纬度带,即第三个纬度带只算一半。三个纬度带从高到底对应的角度分别为 θ , ? , π / 2 ? θ ? ? \theta, \phi, \pi/2-\theta-\phi θ,?,π/2?θ??
- 最高纬度带的面积可以用球冠面积公式得到
S 1 = 2 π r h = 2 π r ( 1 ? c o s θ ) r = 2 π r 2 ( 1 ? c o s θ ) S_1=2\pi rh=2\pi r (1-cos\theta)r=2\pi r^2 (1-cos\theta) S1?=2πrh=2πr(1?cosθ)r=2πr2(1?cosθ) - 根据球冠面积同样可以计算得到第二个纬度带的面积
S 2 = 2 π r 2 ( 1 ? c o s ( θ + ? ) ) ? 2 π r 2 ( 1 ? c o s θ ) = 2 π r 2 ( c o s θ ? c o s ( θ + ? ) ) S_2 = 2\pi r^2(1-cos(\theta+\phi)) - 2\pi r^2 (1-cos\theta) =2 \pi r^2 ( cos\theta - cos(\theta+\phi)) S2?=2πr2(1?cos(θ+?))?2πr2(1?cosθ)=2πr2(cosθ?cos(θ+?)) - 根据半球面积可以计算得到最后半个纬度带的面积
S 2.5 = S 半 球 ? ( S 1 + S 2 ) = 2 π r 2 ? 2 π r 2 ( 1 ? c o s ( θ + ? ) ) = 2 π r 2 c o s ( θ + ? ) S_{2.5} = S_{半球}-(S_1+S_2) = 2\pi r^2 - 2\pi r^2(1-cos(\theta+\phi)) =2 \pi r^2 cos(\theta+\phi) S2.5?=S半球??(S1?+S2?)=2πr2?2πr2(1?cos(θ+?))=2πr2cos(θ+?) - 假设第一个纬度带分
m
m
m块,第二个纬度带分
n
n
n块,最后半个纬度带分
o
o
o块,则要求
2 π r 2 ( 1 ? c o s θ ) m = 2 π r 2 ( c o s θ ? c o s ( θ + ? ) ) n = 2 ? 2 π r 2 c o s ( θ + ? ) o 1 ? c o s θ m = c o s θ ? c o s ( θ + ? ) n = 2 c o s ( θ + ? ) o \frac{2\pi r^2 (1-cos\theta)}{m}=\frac{2 \pi r^2 ( cos\theta - cos(\theta+\phi))}{n}=2*\frac{2 \pi r^2 cos(\theta+\phi)}{o}\\ \frac{1-cos\theta}{m}=\frac{ cos\theta - cos(\theta+\phi)}{n}=\frac{2cos(\theta+\phi)}{o} m2πr2(1?cosθ)?=n2πr2(cosθ?cos(θ+?))?=2?o2πr2cos(θ+?)?m1?cosθ?=ncosθ?cos(θ+?)?=o2cos(θ+?)? - 接下来只要按照想要的划分方式给
m
m
m、
n
n
n和
o
o
o赋整数,就能求解
θ
\theta
θ和
?
\phi
?,例如
- m = 3 , n = 4 , o = 5 , θ = 46.826 ° , ? = 27.916 ° m=3, n=4, o=5, \theta=46.826\degree, \phi=27.916\degree m=3,n=4,o=5,θ=46.826°,?=27.916°
- m = 3 , n = 4 , o = 6 , θ = 45.573 ° , ? = 26.969 ° m=3, n=4, o=6, \theta=45.573\degree, \phi=26.969\degree m=3,n=4,o=6,θ=45.573°,?=26.969°
- m = 4 , n = 5 , o = 6 , θ = 48.190 ° , ? = 27.333 ° m=4, n=5, o=6, \theta=48.190\degree, \phi=27.333\degree m=4,n=5,o=6,θ=48.190°,?=27.333°
| Total Cell | Cells | Latitudinal | Longitudinal |
|---|---|---|---|
| 19 | 3 4 5 4 3 | 0-46.826° 46.826°-74.743° 74.743°-105.257° 105.257°- 133.174° 133.174°-180° | 120° 90° 72° 90° 120° |
| 24 | 4 5 6 5 4 | 0-48.190° 48.190°-75.522° 75.522°-104.478° 104.478°- 131.810° 131.810°-180° | 90° 72° 60° 72° 90° |
c++代码
这里以“统计球形点云落在每个块中的数量”为例,划分方式为 x = 4 , m = 3 , n = 7 x=4, m=3, n=7 x=4,m=3,n=7
/**
* 统计球形点云落在每个块中的数量
* @param[in] points n*3的矩阵,存储三维点云
* @param[out] nums 统计结果,存储顺序北极->南极 & 经度0°->360°
*/
void ClassifyCentroidVector(const Eigen::MatrixXf &points, vector<int> &nums) {
direct.resize(20);
Eigen::Vector4f block_theta(0., 0.7954, 1.5708, 2.3462);
Eigen::Vector4f block_phi(2.0944, 0.8976, 0.8976, 2.0944);
Eigen::Vector4i offset(0, 3, 10, 17);
for (int k = 0; k < points.rows(); k++) {
//笛卡尔坐标系转换为球坐标系
const float x = points(k, 0), y = points(k, 1), z = points(k, 2);
float r = sqrt(x * x + y * y + z * z);
float theta = acos(z / r);
float fai = atan2(y, x) + M_PI; // 取值范围0-2π
int coord_theta = -1;
for(int i = 0; i < block_theta.size(); i++)
if(theta > block_theta(i)){
coord_theta = i;
break;
}
assert(coord_theta != -1);
int coord_phi = int(fai/block_phi(coord_theta));
direct[offset(coord_theta)+coord_phi] += 1;
}
}