[C++知识库]【C++从入门到踹门】第二十篇：布隆过滤器

布隆过滤器

在使用新闻app看新闻时，一旦刷新就会为我们不停地推荐新的内容，他每次推荐时要去重，过滤掉哪些已经浏览过的内容。那么新闻客户端是如何去重的呢？服务器记录了用户看过的所有历史记录，当推荐系统推荐新闻时先对历史记录进行过滤，滤掉重复的内容。那么它又是如何进行快速查找的呢？

我们可以想到如下的方法：

1. 哈希表：用哈希表存储用户记录，缺点：浪费空间；
2. 位图存储记录，缺点：不能解决哈希冲突；
3. 布隆过滤器：哈希与位图的结合

布隆过滤器的概念

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。

相较于传统的List，Set，Map数据结构，此种方式不仅可以提升查询效率，也可以节省大量的内存空间。但是返回的结果是概率性的，而不是确切的。

布隆过滤器是一个大型位图（bit数组）+多个无偏哈希函数。

一个bit数组：

如果我们要映射一个值到布隆过滤器中，则需要使用多个不同的无偏哈希函数来生成多个哈希值，并对每个哈希值所指向的bit位置为1。

无偏哈希函数就是能把元素的hash值计算的比较均匀的哈希函数。

例如针对字符串"Bloom"和三个不同的哈希函数，分别生成哈希值2、5、7，则bit位图可转为：

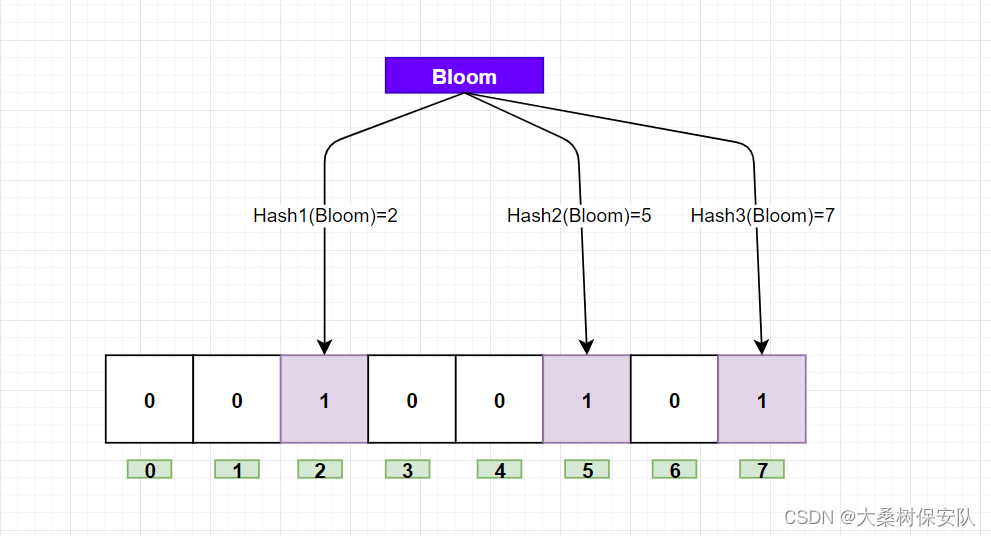
显然，如果我们要查询Bloom这个字符串是否存在，只要这个bit数组中的2、5、7都为1，则大概率存在"Bloom"字符串。

现在我们再存一个值"Filter"哈希函数返回3、6、7，则bit数组变为：

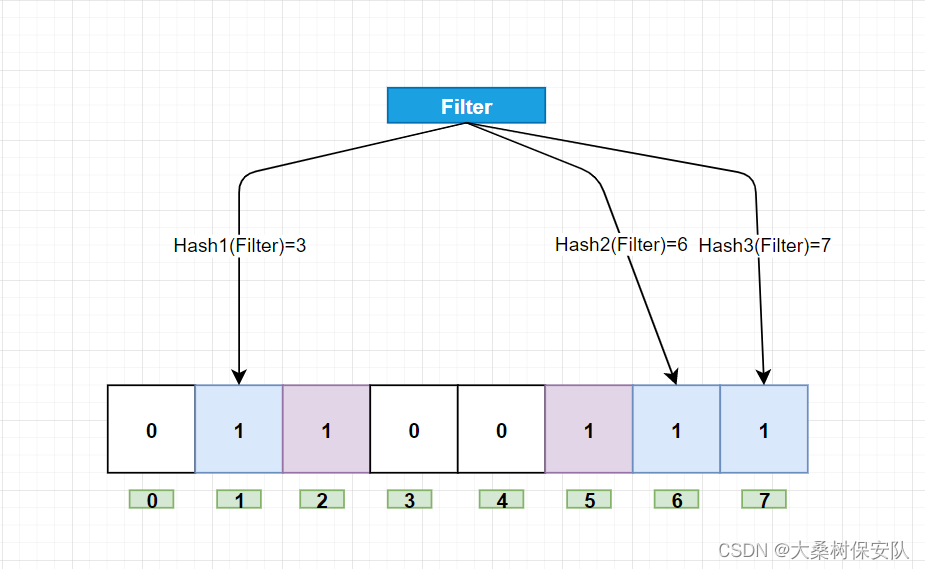
7这个位置的bit位由于哈希值冲突，所以覆盖了。

如果要想查询"Function"这个值是否存在，其哈希值为0、1、2，结果发现0号bit位的值为0，说明没有一个值映射到这个bit位上，因此我们可以确定不存在"Function"这个值。

随着添加的值越来越多，被置为1的bit位也越来越多，这样即使有些值本身并不存在，但是万一哈希函数映射的比特位正好都置为了1，那么他就会被误判为存在。

所以布隆过滤器能告诉我们，某样值只有一定不存在和可能存在。

布隆过滤器使用场景

• 网页URL去重；
• 邮件过滤，使用布隆过滤器来做邮件的黑名单处理；
• 对爬虫网址进行过滤，爬过的不用再爬；
• 解决推荐过的内容不再推荐（短视屏往下滑动不会刷到重复）
• 数据库内置布隆过滤器，如果数据不存在，就减少了数据库的IO请求，因为一旦一个值必定不存在的话，我们可以不用进行后续昂贵的查询请求。

布隆过滤器的优缺点

• 优点

1. 增加和查询元素的时间复杂度为O(K)，K为哈希函数的个数，与数据量大小无关；
2. 哈希函数相互之间没有关系，方便硬件并行运算；
3. 布隆过滤器只需存储状态值，无需存储元素内容，在需要保密的场合有很大优势；
4. 在能够承受一定误判率的情况下，布隆过滤器相较于其他数据结构有很大的空间优势；
5. 使用同一组哈希函数的布隆过滤器可以进行交集，并集和差集运算。

• 缺点

1. 有误判率，即存在假阳性（False Position），不能准确判断元素是否在集合中，且随着元素的增加，误判率会随之升高。
2. 不能获取元素本身
3. 一般情况下不能从布隆过滤器中删除元素
4. 如果采用计数方式删除，可能产生计数回绕问题

🚩关于布隆过滤器中删除元素的问题：

我们很容易想到把比特位数组变为多个bit位数组或者整数数组，每插入一个元素相应的计数器加一，这样删除元素时，将计数器减掉就可以了，然而要保证安全的删除元素并非如此简单，首先我们要保证删除的元素的确在布隆过滤器之中，这一点单凭过滤器便无法保证。

如何选择哈希函数个数和布隆过滤器的长度

如果布隆过滤器过小，很快所有的bit位都会置1，那么查询任何值都是“可能存在”。布隆过滤器的长度会直接影响误报率，布隆过滤器长度与误报率成反比。

并且我们还需考虑哈希函数个数，哈希函数越多映射的位置越多，前期的误报率很低，但是随着而来的是效率的降低，同时布隆过滤器的空间消耗的很快，误报率又会回升。

k为哈希函数的个数，m为布隆过滤器的长度，n为插入的元素的个数，p为误报率。

布隆过滤器的长度和哈希函数的个数可参考公式：

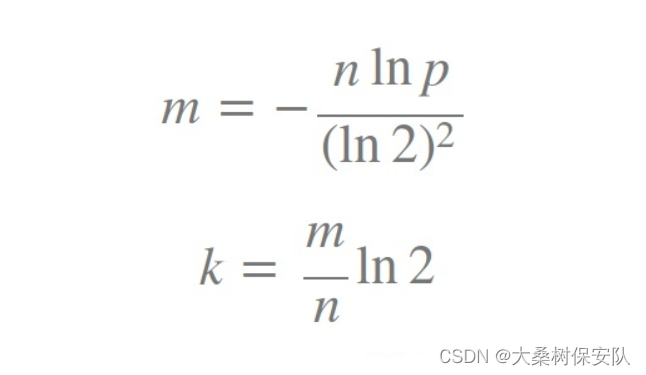
自制简易布隆过滤器

整体框架

底层数据结构选择STL中的 <bitset>

我们如果选用3个哈希函数，通过上述公式计算，布隆过滤器的长度应该设置为可插入容量的4.3倍左右，这里选择取5倍。

template<size_t N,class K=string,class HashFunc1=BKDRHash,class HashFunc2=APHash,class HashFunc3=DJBHash>//映射三个bit位
class BloomFilter
{
private:
	bitset<N*5> _bs;
public:
};

模板参数 N 为可插入元素容量的上限，由用户调用时给出。

之后的模板参数为处理的数据类型，以及相应的哈希函数。如果用户不显式给出，其缺省值将处理string类型的数据。

三个字符串哈希函数如下：他们作为缺省参数。处理字符串类型

struct BKDRHash
{
	size_t operator()(const string& s)
	{
		size_t value=0;
		for (auto ch : s)
		{
			value *= 131l;
			value += ch;
		}
		return value;
	}
};

struct APHash
{
	size_t operator()(const string& s)
	{
		size_t value = 0;
		for (size_t i=0;i<s.size();++i)
		{
			if ((i & 1) == 0)
			{
				value ^= ((value << 7) ^ s[i] ^ (value >> 3));
			}
			else
			{
				value ^= (~(value << 11) ^ s[i] ^ (value >> 5));
			}
		}  
		return value;
	}
};

struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t value = 5381;
		for (auto ch : s)
		{
			value += (value<<5)+ch;
		}
		return value;
	}
};

更多字符串处理函数可参考博文：字符串哈希算法

上述选择的三个字符串哈希函数的冲突率是较低的。

插入

通过哈希函数找到三个位置，再将其bit位图置为1；

public:
	void Set(const K& key)
	{
		int len = 5 * N;
		size_t index1 = HashFunc1()(key) % len;
		size_t index2 = HashFunc2()(key) % len;
		size_t index3= HashFunc3()(key) % len;
		_bs.set(index1);
		_bs.set(index2);
		_bs.set(index3);
	
	}

查找

分别查找映射位，一旦有一个映射位为0，则说明该数据一定不存在。而如果映射位全部为1，说明该数据大概率存在（有可能是其他数据在这些bit位的映射，从而产生误判），所以布隆过滤器只能提供模糊查找，如需精确查询，只能直接查询数据库，但是如果数据不存在则是准确的。

public:
	bool Test(const K& key)
	{
		int len = 5 * N;
		size_t index1 = HashFunc1()(key) % len;
		if (_bs.test(index1) == false)
		{
			return false;
		}
		size_t index2 = HashFunc2()(key) % len;
		if (_bs.test(index2) == false)
		{
			return false;
		}
		size_t index3 = HashFunc3()(key) % len;
		if (_bs.test(index3) == false)
		{
			return false;
		}
		return true;//存在误判
	}

完整代码

#include<iostream>
#include <bitset>
#include <string>
using namespace std;

struct BKDRHash
{
	size_t operator()(const string& s)
	{
		size_t value=0;
		for (auto ch : s)
		{
			value *= 131l;
			value += ch;
		}
		return value;
	}
};

struct APHash
{
	size_t operator()(const string& s)
	{
		size_t value = 0;
		for (size_t i=0;i<s.size();++i)
		{
			if ((i & 1) == 0)
			{
				value ^= ((value << 7) ^ s[i] ^ (value >> 3));
			}
			else
			{
				value ^= (~(value << 11) ^ s[i] ^ (value >> 5));
			}
		}  
		return value;
	}
};

struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t value = 5381;
		for (auto ch : s)
		{
			value += (value<<5)+ch;
		}
		return value;
	}
};

template<size_t N,class K=string,class HashFunc1=BKDRHash,class HashFunc2=APHash,class HashFunc3=DJBHash>//映射三个bit位
class BloomFilter
{
private:
	bitset<N*5> _bs;
public:
	void Set(const K& key)
	{
		//cout << HashFunc1()(key) << endl;
		//cout << HashFunc2()(key) << endl;
		//cout << HashFunc3()(key) << endl;b 
	
		int len = 5 * N;
		size_t index1 = HashFunc1()(key) % len;
		size_t index2 = HashFunc2()(key) % len;
		size_t index3= HashFunc3()(key) % len;
		_bs.set(index1);
		_bs.set(index2);
		_bs.set(index3);
	
	}
	 
	bool Test(const K& key)
	{
		int len = 5 * N;
		size_t index1 = HashFunc1()(key) % len;
		if (_bs.test(index1) == false)
		{
			return false;
		}
		size_t index2 = HashFunc2()(key) % len;
		if (_bs.test(index2) == false)
		{
			return false;
		}
		size_t index3 = HashFunc3()(key) % len;
		if (_bs.test(index3) == false)
		{
			return false;
		}
		return true;//存在误判
	}

};

布隆过滤器的应用

1. 给40亿个整数，没排过序，给一个数，如何快速判断这个数是否在这40个整数之中？

40亿个int=40亿4Bytes=4G4Bytes=16GB，显然这个简单的工作对于内存却是很大的负担。

我们选择使用位图（bitset）来记录一个数据的存在状态，比特位为1则说明存在
，40亿个bit位=512MB
，将占用512MB的内存。

2. 给定100亿个整数，设计算法找到只出现一次的整数？

100亿个整数=10G*4Bytes=40GB，如果使用位图标记则占用512MB。

这种情况下，一个整数就存在3种状态：0次，1次，2次及以上。我们使用两个位图来封装一个类，进行数字出现次数的标记：00——0次，01——1次，11——2次及以上。

3. 给两个文件，分别有100亿个整数，只用1G内存，如何找到两个文件的交集？

分别使用两个位图分别对两个文件的数进行出现状态统计，随后两个位图按位与即可。每个位图占用512MB，两个位图1GB。

4. 1个文件有个100亿个整型，1G内存，设计算法找到出现次数不超过两次的所有整数？

不超过两次，意味着有四种状态：0次、1次、2次、≥3次。

需要用到两个位图进行标记：00——0次，01——1次，10——2次，11——≥3次。

一个位图存放所有4字节范围的整数占512MB，两个文件1G内存。

5. 给两个文件，分别有100亿个query，只用1G内存，如何找到两个文件的交集？分别给出近似算法和精确算法？

query通常为URL的查询字符或者SQL的查询语句，假设每个query占30个字节，那么100亿个query将会占用大量的空间，所以放弃将其放入内存直接对比的方法。

近似算法：使用布隆过滤器，将query使用哈希函数映射到bit位上。该法会有误判的概率，如果一个数据不在布隆过滤器中，则必定不存在，如果存在 于布隆过滤器中，它也未必存在。

精确算法：精确查找只能直接查询数据，由于数据量过大，只能对其进行切割——哈希切割

对于一个文件，我们将其划分为200个小文件，使用哈希函数将query进行哈希映射，映射值为i，然后 i=i%200，将其放入到编号为i的文件中，对两个文件都进行这样的切割，Ai和Bi。

由于使用的是同一个哈希函数，所以相同的query一定会被映射到同一个编号的文件中，所以我们只需按序将编号相同的Ai和Bi放入内存中寻找交集即可。

6. 给一个超过100个G的log file，log存有多个IP地址，设计算法找到出现次数最多的IP地址？以及如何找到出现次数为Top K的IP？如何使用Linux系统指令实现？

使用哈希函数拆分成200份文件， 相同的IP一定进入同一个小文件，那我们可以使用map统计一个小文件的ip的次数，就是它准确的次数（pair<string,int> max_count_ip），遍历每一个文件找到出现次数最大的IP地址。

若寻找Top K，那么可使用优先级队列 priority_queue<pair<string,int>,vector<pair<string,int>>，less>,less仿函数将比较pair中int的大小，使用小堆可满足找最大的K个值的条件。

Linux的指令如下：

sort log_file | uniq -c | sort -nr | head -k

sort log_file对文件进行排序，使得相同的IP地址聚在一起，接着使用uniq -c进行去重，并将重复的次数显示在每列的旁边，通过这个次数来使用sort -nr进行降序排序，使得出现次数最高的IP地址在前面，然后使用head -k获取前k个IP地址。

参考文章：详解布隆过滤器的原理，使用场景和注意事项

拓展：

一致性哈希

哈希与加密

— end —

青山不改 绿水长流