[C++知识库]【GAMES101】作业4 Bézier 曲线

一.作业描述

二.作业解析

1.递归Bezier实现代码

分析了下文档的意思，大概是用递归的方法实现De Casteljau算法。实现起来也比较简单，递归函数的递归出口在control_points中的点数为1时,返回求出的这个点，递归的代码如下所示。

void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) 
{
    // TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
    // recursive Bezier algorithm.


    for (double t = 0.0; t <= 1.0; t += 0.001) 
    {   
        auto point= recursive_bezier(control_points,t);
        std::cout <<  point.x << ", "<< point.y << ")" << '\n';
        window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
    }

}

cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t) 
{
    // TODO: Implement de Casteljau's algorithm
    if(control_points.size()==1){return control_points[0];} 
    std::vector<cv::Point2f> v;
    for(int i=0;i<control_points.size()-1;i++)
    {
        cv::Point2f p=t*control_points[i]+(1-t)*control_points[i+1];
        v.push_back(p);
    }    
    return recursive_bezier(v,t);

}

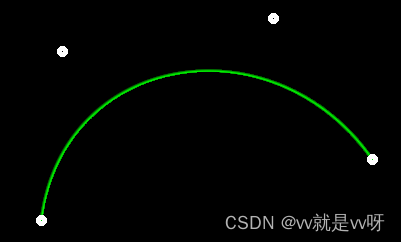
直接调用原代码给出的native_bezier。

两个函数一起调用效果如下所示。

2.Bezier曲线反走样

直接绘制除的Bezier曲线存在走样的问题。

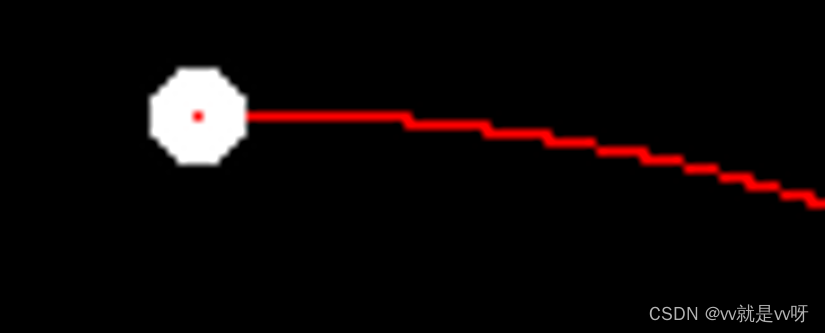
反走样的思路是计算九宫格中与当前点相邻的8个像素点坐标与当前点坐标距离，并根据距离设置颜色线性渐变（思路参考作业4（提高）含Bazier曲线的反走样处理）按照这个思路绘制的边缘效果比其他方法都更强一些。

void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) 
{
    // TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
    // recursive Bezier algorithm.


    for (double t = 0.0; t <= 1.0; t += 0.001) 
    {   
        auto point= recursive_bezier(control_points,t);
        std::cout <<  point.x << ", "<< point.y << ")" << '\n';
        for(int i=-1;i<=1;i++){
            for(int j=-1;j<=1;j++){
                cv::Point2f t;
                t.x=point.x+i;
                t.y=point.y+j;
                float d=sqrt(pow(t.x-((int)t.x+i)-0.5,2)+pow(t.y-((int)t.y+j)-0.5,2));
                float ratio=1.0-sqrt(2)/3.0*d;
                window.at<cv::Vec3b>(t.y, t.x)[1] = std::fmax(255*ratio,window.at<cv::Vec3b>(t.y, t.x)[1]);
            }
        }
        // window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
    }

}

反走样效果如下所示，比起之前的效果要流畅很多。