前言

主要探究递推和递归之间的关系

提示：以下是本篇文章正文内容，本人可能有理解不到位的地方，请批评指正。

一、递推原理

1.递推概念

指从已知条件出发，依据某种递推关系，逐次推出所要求的各中间结果及最后结果。其中初始条件或是问题本身已经给定，或是通过对问题的分析与化简后确定。

2.递推关系

指一个问题的结果与其子问题的结果之间的关系。

3.递推特点

可用递推算法求解的题目一般有以下两个特点：
1)问题可以划分成多个状态；
2)除初始状态外，其它各个状态都可以用固定的递推关系式表示。

4.递推详例

帕斯卡三角形是排列成三角形的一系列数字。在帕斯卡三角形中，每一行的最左边和最右边的数字总是1。对于其余的每个数字都是前一行中直接位于它上面的两个数字之和。
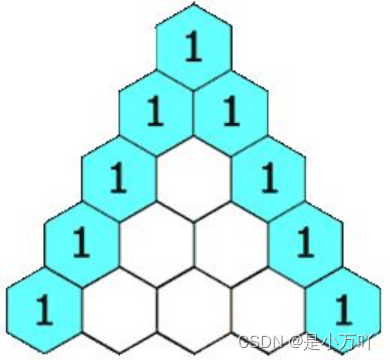
在这里插入图片描述

首先，我们定义一个函数 f(i,j)，它将会返回帕斯卡三角形第i行、第j列的数字。然后，我们可以用下面的公式来表示这一递推关系：f(i,j)=f(i?1,j?1)+f(i?1,j)。

5.解决递推问题的步骤

1)建立递推关系式；(问题可以划分成多个状态；除初始状态外，其它各个状态都可以用固定的递推关系式来表示。实际解题中，题目不会直接给出递推关系式，而是需要通过分析各种状态，找出递推关系式。)
2)确定边界条件；
3)递推求解。

二、递归原理

1.递归的概念

递归指的是在函数的定义中使用函数自身的方法。但在使用递归时，程序员需要注意定义一个从函数退出的条件，否则会进入死循环。递归函数在解决许多数学问题上起了至关重要的作用，比如计算一个数的阶乘、生成斐波那契数列等。

2.构成递归的条件

1)子问题须与原始问题为同样的事，且更为简单；
2)具有终止条件，也就是递归不能无限制地调用本身，须有个出口，化简为非递归状况处理。并且终止条件必须是在递归最开始的地方。

3.递归的模板

1.void recursion()  
2.{  
3.   statements;  
4.   ... ... ...  
5.   recursion(); /* 函数调用自身 */  
6.   ... ... ...  
7.}  
8.   
9.int main()  
10.{  
11.   recursion();  
12.}

4.递归详例

(1)问题描述
斐波那契数列：1、1、2、3、5、8、13、21…，即第一项 f(1) = 1,第二项 f(2) = 1…,第 n 项目为 f(n) = f(n-1) + f(n-2)。求第 n 项的值是多少。
在这里插入图片描述
(2)问题分析
1)先确定f(n)的功能是求第n项的值；
2)当 n = 1或者 n = 2 ,我们可以轻易地知道结果f(1)=f(2)=1。所以递归结束条件可以为n<= 2 时，f(n)==1；
3)由题目可知f(n) = f(n-1) + f(n-2)。
(3)代码示例

1.#include <stdio.h>  
2.int Fibon1(int n)  
3.{  
4.    if (n == 1 || n == 2)  
5.    {  
6.        return 1;  
7.    }  
8.    else  
9.    {  
10.        return Fibon1(n - 1) + Fibon1(n - 2);  
11.    }  
12.}  
13.int main()  
14.{  
15.    int n = 0;  
16.    int ret = 0;  
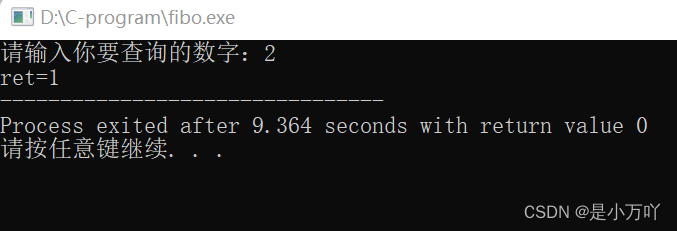
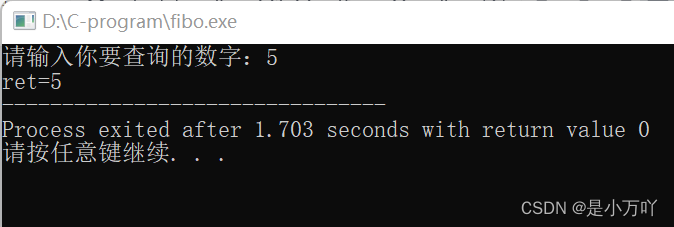
17.    printf("请输入你要查询的数字：");  
18.    scanf("%d", &n);  
19.    ret = Fibon1(n);   
20.    printf("ret=%d", ret);  
21.    return 0;  
22.}

运行结果：
在这里插入图片描述

三、递推和递归都可实现的算法

1.问题描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
在这里插入图片描述

2.问题分析

首先设跳上n级台阶有f(n)种跳法。在所有跳法中，青蛙的最后一步只有两种情况：跳上1级或2级台阶。
1)当为一级台阶时：剩下n-1阶台阶，此时有f(n-1)种跳法；
当为二级台阶时：剩下n-2阶台阶，此时有f(n-2)种跳法。

3.递归实现

1.#include <stdio.h>  
2.int Fn(int n) {  
3.    if (n <= 2) {  
4.        return n;  
5.    }  
6.    else if (n > 2) {  
7.        return Fn(n - 1) + Fn(n - 2);  
8.    }  
9.}  
10.int main() {  
11.    int n = 0;  
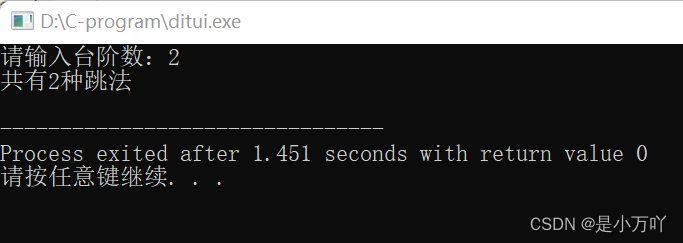
12.    printf("请输入台阶数：");  
13.    scanf("%d", &n);  
14.    printf("共有%d种跳法\n", Fn(n));  
15.    return 0;  
16. }

运行结果：
在这里插入图片描述

4.递推实现

1.#include <stdio.h>  
2.int Fn(int n) {  
3.    int a = 1;  
4.    int b = 2;  
5.    int c = 0;  
6.    if (n == 1) {  
7.        return 1;  
8.    }  
9.    else if (n == 2) {  
10.        return 2;  
11.    }  
12.    else {  
13.        for (int i = 3;i <= n;i++) {  
14.            c = a + b;  
15.            a = b;  
16.            b = c;  
17.        }  
18.        return c;  
19.    }  
20.}  
21.int main() {  
22.    int n = 0;  
23.    printf("请输入台阶数：");  
24.    scanf("%d", &n);  
25.    printf("共有%d种跳法\n", Fn(n));  
26.    return 0;  
27.}

四、递推和递归的优缺点

1.递推的优缺点

1)优点
a.可以从已知的问题着手，推测出未知的状态；
b.在问题规模较大时，性能优于递归。
2)缺点
a.存在多次循环；
当问题规模较简单时，性能较差。

2.递归的优缺点

1)优点
a.有更好的可读性和可维护性；
b.复杂问题用递归解决问题比循环更加简便；
c.某些问题只能用递归解决。
2)缺点
a.递归通常会出现很多次重复计算，导致时间复杂度提高；
b.在边界条件设置不当的情况下很有可能陷入死循环或者内存溢出的情况；
c.调用栈时可能会溢出，每一次函数调用都会在内存栈中分配空间，而每个进程的栈的容量都是有限的，当调用的层次太多时，就会超出栈的容量，从而导致栈溢出。