An integer sequence with length?nn, denoted by?a_1,a_2,\cdots,a_na1?,a2?,?,an?, is generated randomly, and the probability of being?1,2,\cdots,n1,2,?,n?are all?\frac{1}{n}n1??for each?a_iai??(i=1,2,\cdots,n)(i=1,2,?,n).
Your task is to calculate the expected number of permutations?p_1,p_2,\cdots,p_np1?,p2?,?,pn??from?11?to?nn?such that?p_i \le a_ipi?≤ai??holds for each?i=1,2,\cdots,ni=1,2,?,n.
Input
The only line contains an integer?nn?(1 \leq n \leq 50)(1≤n≤50).
Output
Output the expected number of permutations satisfying the condition. Your answer is acceptable if its absolute or relative error does not exceed?10^{-9}10?9.
Formally speaking, suppose that your output is?xx?and the jury's answer is?yy. Your output is accepted if and only if?\frac{|x - y|}{\max(1, |y|)} \leq 10^{-9}max(1,∣y∣)∣x?y∣?≤10?9.
| Inputcopy | Outputcopy |
|---|---|
2 | 1.000000000000 |
Sample 2
| Inputcopy | Outputcopy |
|---|---|
3 | 1.333333333333 |
Sample 3
| Inputcopy | Outputcopy |
|---|---|
50 | 104147662762941310907813025277584020848013430.758061352192 |
题意:长度为n的a数组中,每个数是1,2,3,4..n的概率都是1/n,对于全排列的p数组(如1,2,3。1,3,2。2,1,3。2,3,1。3,1,2。3,2,1),全部下标i都成立的pi<ai的数学期望是多少。
题意比较难懂,就是所有全排列的p数组答案+起来,p数组为1,2答案2/4,因为a数组有1,2。2,2可以,两个的概率是2/2*2=0.5,p数组为2,1的答案也是0.5,最后就是1.000000。
思路:答案简单算算可以知道为:(n!*n!)/n^n。没有公式直接算即可。
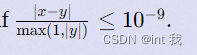 ,他的意思应该是前10位对就ok,所以c++的long double和py直接小数计算都可
,他的意思应该是前10位对就ok,所以c++的long double和py直接小数计算都可
?代码:
#include<bits/stdc++.h>
using namespace std;
#define fo(a,b) for(int i=a;i<=b;i++)
#define inf 0x3f3f3f3f
#define dou long double
#define M 100005
dou res=1,n;
int main(){
cin>>n;
for(dou i=1;i<=n;i++){
res*=i*i/n;
}
printf("%.15Lf\n",res);
return 0;
}
py代码:
n=(int)(input())
res=1
for i in range(1,n+1):
res*=1.0/n*i*i
print(res)