文章目录
一、AVL树的旋转规则
1.AVL树概述(示意图)
AVL树是为了解决BST(二叉搜索树)树在一些情况下树的形状退化成线性链表而诞生的一种树。它有着BST树的特点(中序遍历是顺序的),但是有新的特点:对于每个节点来说,左右子树的高度差小于等于1.因此,AVL树是高度平衡的二叉搜索树。为了保持平衡,在四种情况下,树的结构要进行变形。这四种情况分别为:
- 左孩子的左子树太高
- 右孩子的右子树太高
- 左孩子的右子树太高
- 右孩子的左子树太高
在发生上面四种情况时,则需要变形操作。变形的操作分为左旋和右旋。
- 通过左旋,能让情况2变成平衡。
- 通过右旋,能让情况1变成平衡。
- 通过左平衡(左旋加右旋),能让情况3平衡。
- 通过右平衡(右旋加左旋),能让情况4平衡。
下面是四种情况的示意图:
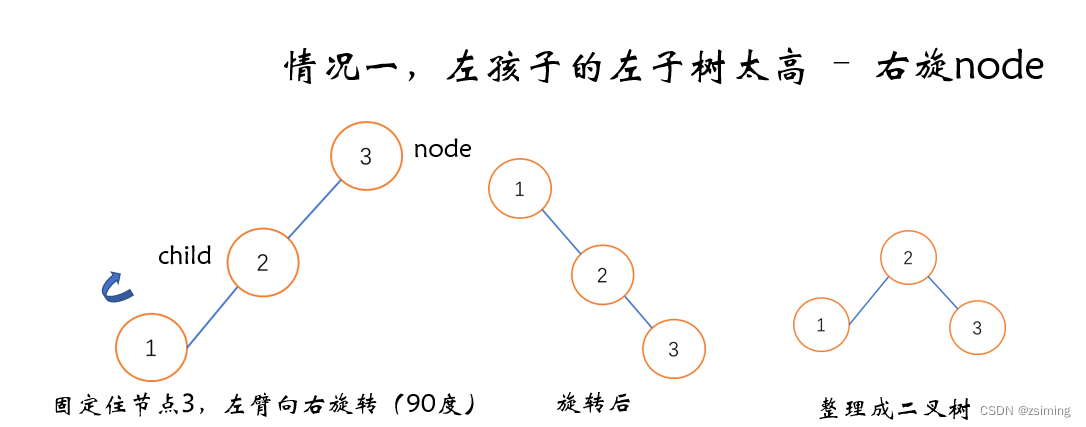
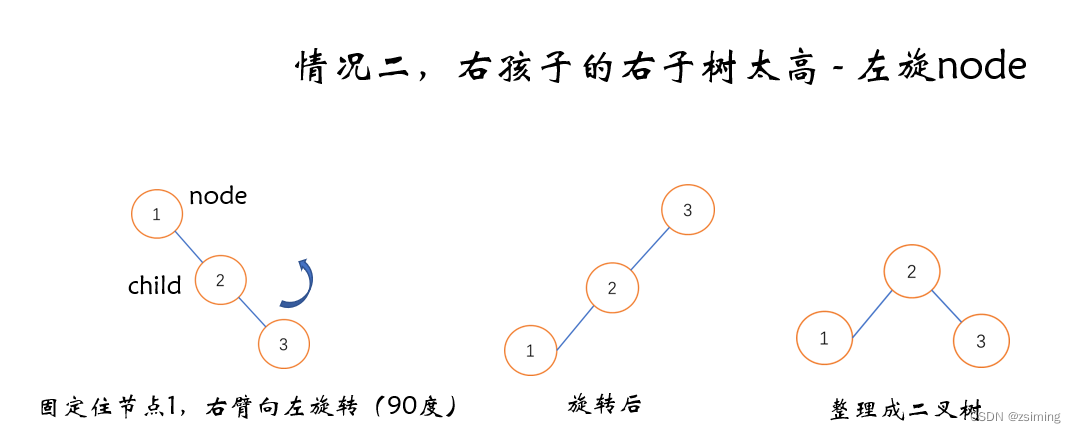
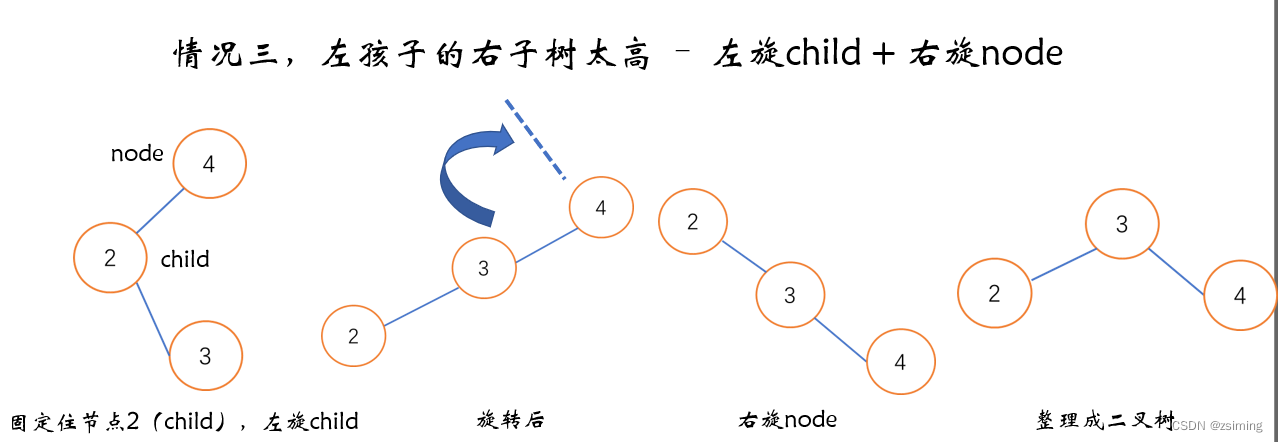
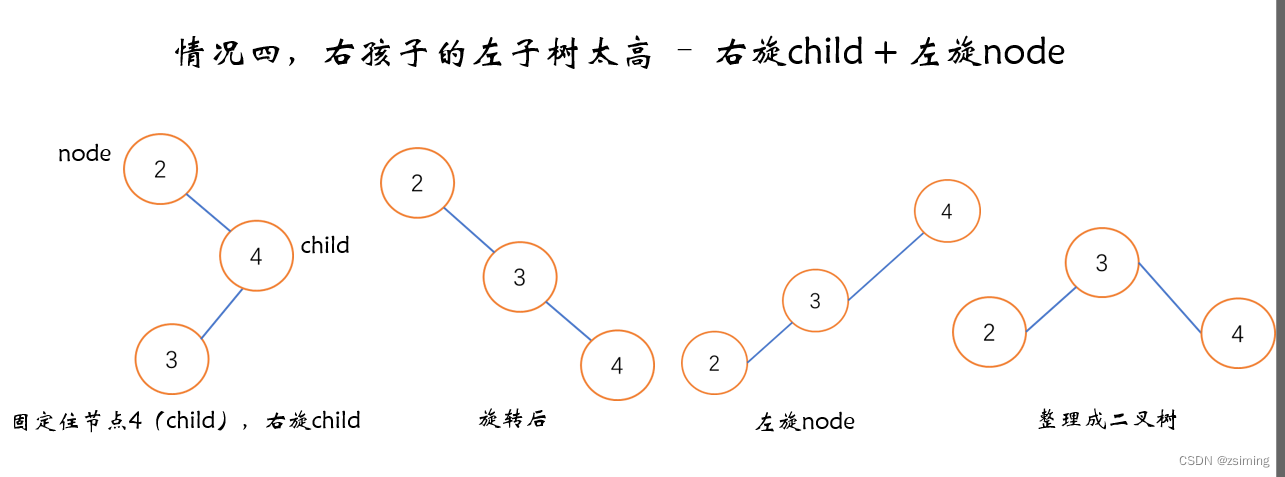
2. 四种操作的代码:
2.1 左旋
// 左旋
Node* leftRotate(Node* node) {
Node* child = node->right;
node->right = child->left;
child->left = node;
// 更新高度
node->_height = max(height(node->left), height(node->right)) + 1;
child->_height = max(height(child->left), height(child->right)) + 1;
return child;
}
2.2 右旋
//右旋
Node* rightRoate(Node* node) {
Node* child = node->left;
node->left = child->right;
child->right = node;
// 更新高度
node->_height = max(height(node->left), height(node->right)) + 1;
child->_height = max(height(child->left), height(child->right)) + 1;
return child;
}
2.3 左平衡(左旋+右旋)
//左平衡: 左孩子的右子树太高
Node* leftBalance(Node* node) {
node->left = leftRotate(node->left);
return rightRoate(node);
}
2.4 右平衡
//右平衡:右孩子的左子树太高
Node* rightBalance(Node* node) {
node->right = leftRotate(node->right);
return rightRoate(node);
}
二、AVL树的实现
AVL树的重点在于插入和删除操作。
1.插入操作
- AVL树的插入和BST树的插入一样,
都是通过深度遍历来实现的。不同的地方是AVL树在每层递归结束之后,都会检查当前的节点是否满足高度平衡这个条件。如果不满足,就使用左右旋转或左右平衡来让当前节点平衡。
2.插入操作代码
// 内部的插入操作
Node* insert(Node* node, const int& val) {
if (node == nullptr) {
return new Node(val);
}
if (node->_val > val) {
node->left = insert(node->left, val);
// 调整高度
if (height(node->left) - height(node->right) > 1) {
if (height(node->left->left) >= height(node->left->right)) {
node = rightRoate(node);
} else {
node = leftBalance(node);
}
}
} else if (node->_val < val) {
node->right = insert(node->right, val);
// 调整高度
if (height(node->right) - height(node->left) > 1) {
if (height(node->right->right) >= height(node->right->left)) {
node = leftRotate(node);
} else {
node = rightBalance(node);
}
}
} else {
; //已经有该节点了,不做任何操作
}
node->_height = max(height(node->left), height(node->right)) + 1;
return node;
}
3.删除操作
AVL树的删除是通过二分搜索实现的。在找到需要删除的节点后,可以分为三种情况:
- 待删除的节点有左右孩子
- 待删除的节点只有左孩子
- 待删除的节点只有右孩子
如果删除的节点有左右孩子,那么为了减少旋转操作:我们可以找出待删除节点究竟是左子树比较高还是右子树比较高。如果是左子树比较高,我们就把待删除节点的前驱节点(最后一个大于待删除节点的节点)数据覆盖到待删除节点上,再删除前驱节点。反之,我们就把待删除节点的后继节点(第一个大于待删除节点的节点)覆盖到待删除节点上,再删除后继节点。
而如果只有左右孩子的话,就比较简单:待删除节点释放后,把左右孩子返回即可。
完成了删除操作之后,我们在每层回溯时来检查每个节点的左右子树高度是否平衡。如果不平衡,就使用左右旋转或左右平衡来让当前节点平衡。
2.插入操作代码
// 内部的删除操作
Node* remove(Node* node, const int& val) {
if (node == nullptr) return nullptr;
if (node->_val > val) {
node->left = remove(node->left, val);
// 已经删除完毕,在回溯中检查左子树有没有因为删除而失衡
if (height(node->right) - height(node->left) > 1) {
if (height(node->right->right) >= height(node->right->left)) {
node = leftRotate(node);
} else {
node = rightBalance(node);
}
}
} else if (node->_val < val) {
node->right = remove(node->right, val);
// 已经删除完毕,在回溯中检查右子树有没有因为删除而失衡
if (height(node->left) - height(node->right) > 1) {
if (height(node->left->left) >= height(node->left->right)) {
node = rightRoate(node);
} else {
node = leftBalance(node);
}
}
} else {
// 1.存在左右孩子
if (node->left && node->right) {
// 如果左子树比右子树高就用前驱补到node的位置
if (height(node->left) >= height(node->right)) {
Node* pre = node->left;
while (pre->right != nullptr) {
pre = pre->right;
}
// 将前驱的数据覆盖到当前节点中
node->_val = pre->_val;
// 删除前驱
node->left = remove(node->left, pre->_val);
} else {
// 如果左子树比右子树矮就用后继补到node的位置
Node* post = node->right;
while (post->left != nullptr) {
post = post->left;
}
// 将后继的数据覆盖到node的位置
node->_val = post->_val;
// 删除后继
node->right = remove(node->right, post->_val);
}
} else {
// 2.只存在左孩子
if (node->left != nullptr) {
Node* tmp = node->left;
delete node;
return tmp;
}
// 3.只存在右孩子
if (node->right != nullptr) {
Node* tmp = node->right;
delete node;
return tmp;
}
// 4.没有左孩子和没有右孩子
if (node->left == nullptr && node->right == nullptr) {
delete node;
return nullptr;
}
}
}
node->_height = max(height(node->left), height(node->right)) + 1;
return node;
}
3、完整实现
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
struct Node {
Node* left;
Node* right;
int _val;
int _height;
Node(int val) : _val(val), _height(1), left(nullptr), right(nullptr) {}
};
class AVLTree {
private:
Node* _root;
// 得到树的高度
int height(Node* node) {
return node ? node->_height : 0;
}
// 左旋
Node* leftRotate(Node* node) {
Node* child = node->right;
node->right = child->left;
child->left = node;
// 更新高度
node->_height = max(height(node->left), height(node->right)) + 1;
child->_height = max(height(child->left), height(child->right)) + 1;
return child;
}
//右旋
Node* rightRoate(Node* node) {
Node* child = node->left;
node->left = child->right;
child->right = node;
// 更新高度
node->_height = max(height(node->left), height(node->right)) + 1;
child->_height = max(height(child->left), height(child->right)) + 1;
return child;
}
//左平衡: 左孩子的右子树太高
Node* leftBalance(Node* node) {
node->left = leftRotate(node->left);
return rightRoate(node);
}
//右平衡:右孩子的左子树太高
Node* rightBalance(Node* node) {
node->right = leftRotate(node->right);
return rightRoate(node);
}
// 内部的插入操作
Node* insert(Node* node, const int& val) {
if (node == nullptr) {
return new Node(val);
}
if (node->_val > val) {
node->left = insert(node->left, val);
// 调整高度
if (height(node->left) - height(node->right) > 1) {
if (height(node->left->left) >= height(node->left->right)) {
node = rightRoate(node);
} else {
node = leftBalance(node);
}
}
} else if (node->_val < val) {
node->right = insert(node->right, val);
// 调整高度
if (height(node->right) - height(node->left) > 1) {
if (height(node->right->right) >= height(node->right->left)) {
node = leftRotate(node);
} else {
node = rightBalance(node);
}
}
} else {
; //已经有该节点了,不做任何操作
}
node->_height = max(height(node->left), height(node->right)) + 1;
return node;
}
// 内部的删除操作
Node* remove(Node* node, const int& val) {
if (node == nullptr) return nullptr;
if (node->_val > val) {
node->left = remove(node->left, val);
// 已经删除完毕,在回溯中检查左子树有没有因为删除而失衡
if (height(node->right) - height(node->left) > 1) {
if (height(node->right->right) >= height(node->right->left)) {
node = leftRotate(node);
} else {
node = rightBalance(node);
}
}
} else if (node->_val < val) {
node->right = remove(node->right, val);
// 已经删除完毕,在回溯中检查右子树有没有因为删除而失衡
if (height(node->left) - height(node->right) > 1) {
if (height(node->left->left) >= height(node->left->right)) {
node = rightRoate(node);
} else {
node = leftBalance(node);
}
}
} else {
// 1.存在左右孩子
if (node->left && node->right) {
// 如果左子树比右子树高就用前驱补到node的位置
if (height(node->left) >= height(node->right)) {
Node* pre = node->left;
while (pre->right != nullptr) {
pre = pre->right;
}
// 将前驱的数据覆盖到当前节点中
node->_val = pre->_val;
// 删除前驱
node->left = remove(node->left, pre->_val);
} else {
// 如果左子树比右子树矮就用后继补到node的位置
Node* post = node->right;
while (post->left != nullptr) {
post = post->left;
}
// 将后继的数据覆盖到node的位置
node->_val = post->_val;
// 删除后继
node->right = remove(node->right, post->_val);
}
} else {
// 2.只存在左孩子
if (node->left != nullptr) {
Node* tmp = node->left;
delete node;
return tmp;
}
// 3.只存在右孩子
if (node->right != nullptr) {
Node* tmp = node->right;
delete node;
return tmp;
}
// 4.没有左孩子和没有右孩子
if (node->left == nullptr && node->right == nullptr) {
delete node;
return nullptr;
}
}
}
node->_height = max(height(node->left), height(node->right)) + 1;
return node;
}
public:
AVLTree() : _root(nullptr) {}
// 得到头部节点
Node* getHead() {
return _root;
}
// 用户调用的插入操作
void insert(const int& val) {
_root = insert(_root, val);
}
// 用户调用的删除操作
void remove(const int& val) {
_root = remove(_root, val);
}
};
void printTree(Node* root) {
queue<Node*> que;
if (root) que.push(root);
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; ++i) {
Node* cur = que.front(); que.pop();
cout << cur->_val << " ";
if (cur->left) que.push(cur->left);
if (cur->right) que.push(cur->right);
}
cout << endl;
}
}
int main() {
{
// 测试左旋
AVLTree tree;
for (int i = 0; i < 10; ++i) {
tree.insert(i);
}
// 打印二叉树
Node* head = tree.getHead();
printTree(head);
// 测试删除操作
tree.remove(7);
tree.remove(4);
tree.remove(5);
tree.remove(6);
head = tree.getHead();
printTree(head);
}
// 测试右旋
/*{
AVLTree tree;
for (int i = 10; i >= 0; --i) {
tree.insert(i);
}
Node* head = tree.getHead();
printTree(head);
}*/
return 0;
}