质数
在大于1的整数中,只有1和本身两个约数,则称为素数(质数)。
1.质数的判断(试除法)
int prime(long long n)
{
??? if(n<2) return 0;//要求大于1 的正整数
??? else
??? {
??????? for(int i=2;i<n;i++)//遍历一遍,时间复杂度妥妥的O(n)超时
??????? {
??????????? if(n%i==0) return 0;
??????? }
??? }
??? return 1;
}优化一下:
由于n/d=x,同时n/x=d也成立,所以可以得出约数是成对存在的。
由此我们只需要枚举一下较小的的那个,即d<=n/d,把循环条件改写成i<=n/i,这样时间复杂度就为O(sqrt(n))了。
?题面:
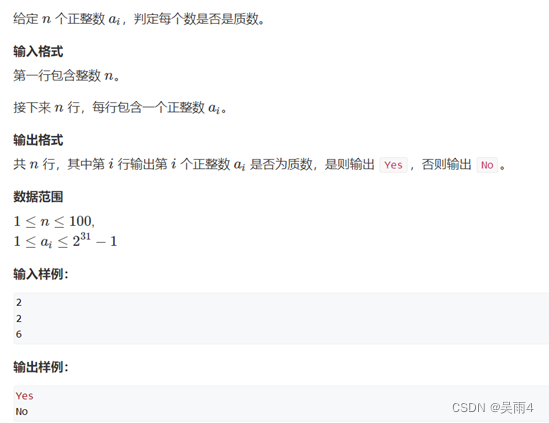
2.分解质因数(试除法)
质因数是指能整除给定整除的质数因子。
【若两个数只有1一个共同的质因子,称为互质】
【1和任何一个正整数都是互为质数】
【任何一个数都可以看成多个质因子相乘,n=p1^k1*p2^k2*…*pn^kn】
题面:
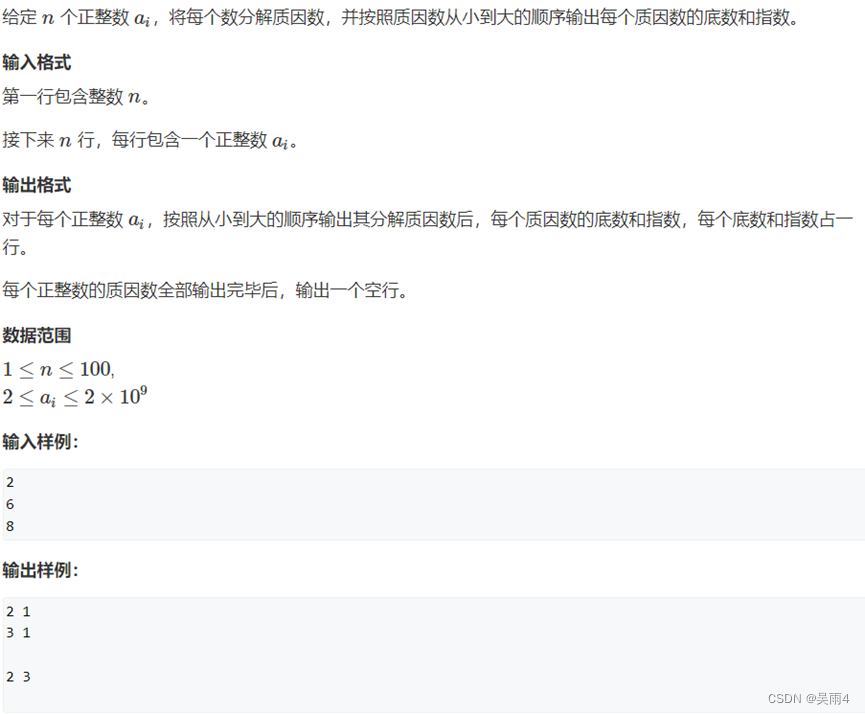
?代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll t;
cin>>t;
while(t--)
{
ll n;
cin>>n;
for(int i=2;i<=n;i++)//时间复杂度是O(n),超时咯
{
if(n%i==0)//看似是找出来的是n的因数,而非质因数。
/*但其实这里没问题,由于下面一旦找到了能被整除的i,n会进入循环一直除i知道除不了为止。拿4来举例子,在i=2的时候就n/=2 ——>n=2,又n/=2——>n=0.没有i=4什么事了,所以把因数为合数的情况全部除尽了,保证都是质因数。*/
{
int s=0;
while(n%i==0)//找出指数为多少
{
n/=i;
s++;
}
cout<<i<<" "<<s<<endl;
}
}
cout<<endl;//输出有每个数据要换行的要求
}
return 0;
}
优化一下:
由于n中最多只有一个大于sqrt(n)的质因子
因此循环条件换成i<=n/i,同时加上一个特判if(n>1) cout<<n<<" "<<1<<endl;
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll t;
cin>>t;
while(t--)
{
ll n;
cin>>n;
for(int i=2;i<=n/i;i++)//时间复杂度为O(sqrt(n)),最多为sqrt(n)
{
if(n%i==0)
{
int s=0;
while(n%i==0)
{
n/=i;
s++;
}
cout<<i<<" "<<s<<endl;
}
}
if(n>1) cout<<n<<" "<<1<<endl;
cout<<endl;
}
return 0;
}
3.筛质数

题目链接:868. 筛质数 - AcWing题库
题面:

代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
int primes[N],cnt,n;
bool st[N];
int main()
{
??? cin>>n;
??? for(int i=2;i<=n;i++)
??? {
??????? if(!st[i])//依次从小到大质数遍历,最小的为2
??????????? primes[cnt++]=i;
??????? for(int j=i+i;j<=n;j+=i)//把i的倍数都删掉
??????????? st[j]=true;
??? }
??? cout<<cnt<<endl;
??? return 0;
}时间复杂度计算:
n/2+n/3+n/4+…+n/n
=n(1/2+1/3+1/4+…+1/n)
当n趋于正无穷时,后面为调和级数,值为ln n+c (c为0.57)
又因为ln n<log2 n
所以时间复杂度为:O(nlog2 n)
优化一下:把第二个循环放到if里面去,就是埃氏筛法
具体的埃氏筛法传送门:
埃拉托色尼筛选法巧解质数问题(埃氏筛法求解素数问题)_吴雨4的博客-CSDN博客
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
int primes[N],cnt,n;
bool st[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=2;i<=n;i++)
{
if(!st[i])//依次从小到大质数遍历,最小的为2
{
primes[cnt++]=i;
for(int j=i+i;j<=n;j+=i)//把i的倍数都删掉
st[j]=true;
}
}
cout<<cnt<<endl;
return 0;
}

?两次都能AC,但是第二个筛法比第一个快了五倍。
?还有一种线性筛法:(数据范围为1e7时比埃氏筛法又快了一倍)
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
int primes[N],cnt,n;
bool st[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=2;i<=n;i++)
{
if(!st[i])//依次从小到大质数遍历,最小的为2
primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0) break;
}
}
cout<<cnt<<endl;
return 0;
}