[C++知识库]欧拉函数的实现（C语言）

?我们先来看个例子：

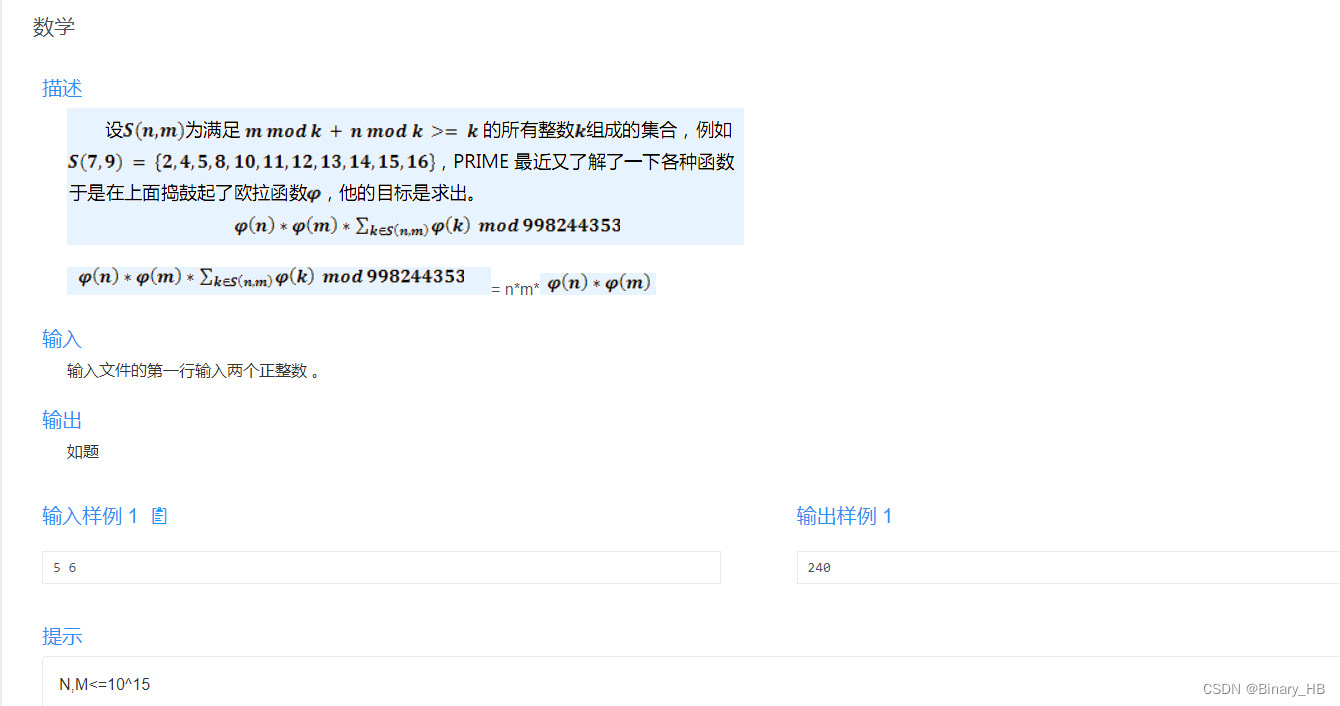
?前面这一堆话其实对解题没有任何帮助，这个题目其实是要我们直接输出n*m*φ（n）*φ（m）的结果。其中φ（n）是欧拉函数。

首先我们看看什么是欧拉函数:

一.什么是欧拉函数
欧拉函数就是指：对于一个正整数n，小于或等于n的正整数中与n互质的正整数个数（包括1）的个数，记作 φ ( n )

二.欧拉函数的一些性质
若n为质数，则φ ( n ) = n - 1;
若m与n互质，则φ ( n*m ) = φ ( n ) * φ ( m );
若正整数n与a互质，那么就有
若n为奇数时，φ ( 2n ) = φ ( n );
若n = pk且p是质数，那么φ ( n ) = (p - 1) * pk-1 = pk - pk-1.

原文链接：https://blog.csdn.net/weixin_45843077/article/details/108741889

我们再来看看什么是互质数;

互质数就是指两个数的最大公约数只有1。例如6和3的最大公约数是3，它们不是互质数；10和9的最大公约数为1，它们互为质数。

那么如何证明两个数字是否为互质数：

我这里用到的是欧几里得的辗转相除法

大致思想是：

1 首先设r为a/b所得余数即 r = a % b （0≤r<b）

?2? 如果r= 0，程序结束；b 即为最大公约数。

3? 如果r!= 0?：则将b赋给a， r赋给b ，又返回执行第一步。

int fun(int m,int n)
{
    int mod;
    mod=m%n;
    while(mod!=0)
    {
        a=b;
        b=mod;
        mod=a%b;
    }
    return n;
}

?

接下来就是整个代码段

?
#include<iostream>
#include<math.h>
#define size 1000
using namespace std;
int zhishu(int n)//判断是否为质数
{
    int flag=0;
    for(int i=2; i<sqrt(n); i++)
    {
        if (n%i==0)
            flag++;
    }
    if(n!=1&&flag==0)
        return 1;//是质数
    else
        return 0;
}
int func(int n)//欧拉函数的实现函数
{
    if(zhishu(n))
        return n-1;
    int sum=0;
    for(int j=1; j<n; j++)//欧几里得算法
    {
        int m=n;
        int i=j;
        int mod;//余数；
        while(i!=0)
        {
            mod=m%i;
            m=i;
            i=mod;
        }
        if(m==1)
            sum++;
    }
    return sum;
}
int main()
{
    long long l,r;
    cin>>l>>r;
    cout<<l*r*func(l)*func(r);
    return 0;
}

?