17.4 树
?? ?描述一种非常有用的树:二叉树搜索树(binary search tree),可以很好地说明实现树的技巧。
?? ?树是一种数据结构,它要么为空,要么具有一个值并具有零个或多个孩子(child),每个孩子本身也是树。这个递归的定义正确地提示了一棵树的高度并没有内在的限制。二叉树(binary tree)是树的一种特殊形式,它的每个节点至多具有两个孩子,分别称为左孩子(left)和右孩子(right)。二叉搜索树具有一个额外的属性:每个节点的值比它的左子树所有结点的值都要大,但比它的右子树所有结点都要小。
?? ?注意,这个定义排除了树中存在值相同的节点的可能性。这些属性使二叉搜索树成为一种用关键值快速查找数据的优秀工具。图17.1是二叉搜索树的一个例子。这棵树的每个节点正好具有一个双亲节点(它的上层节点),并有零个、一个或两个孩子(直接在它下面的节点)。
?? ?唯一的例外是最上面的那个节点,称为树根,它没有双亲结点。没有孩子的节点被称为叶节点(leaf node)或叶子(leaf)。在绘制树时,根位于顶端,叶子位于底部。(注意,这和自然世界中根在底,叶在上的树实际上是颠倒的。)
?? ?17.4.1 在二叉搜索树中插入
?? ?当一个新值添加到一棵二叉搜索树时,它必须被放在合适的位置,继续保持二叉搜索树的属性。幸运的是,这个任务是很简单的。基本算法如下所示:
?? ?如果树为空:
?? ??? ?把新值作为根节点插入
?? ?否则:
?? ??? ?如果新值小于当前节点的值:
?? ??? ??? ?把新值插入到当前节点的左子树
?? ??? ?否则:
?? ??? ??? ?把新值插入到当前节点的右子树
?? ?这个算法的递归表达式正是树的递归定义的直接结果。
?? ?提示:
?? ?由于递归在算法的尾部出现(尾部递归),因此可以使用迭代更有效地实现这个算法。
?? ?17.4.2 从二叉树搜索树删除节点
?? ?从树中删除一个值比从堆栈或队列中删除一个值更为困难。从一棵树的中部删除一个节点将导致它的子树和树的其余部分断开---必须重新连接它们,否则它们将会丢失。
?? ?我们必须处理3种情况:删除没有孩子的节点;删除只有一个孩子的节点;删除有两个孩子的节点。第一种情况很简单,删除一个叶节点不会导致任何子树断开,所以不存在重新连接的问题。删除只有一个孩子的节点几乎同样简单:把这个节点的双亲结点和它的孩子连接起来就可以了。这个解决方法防止了子树的断开,而且仍能维持二叉搜索树的次序。最后一种情况要困难得多。如果一个节点有两个孩子,则它的双亲不能连接到它的两个孩子。解决这个问题的一种策略是不删除这个节点,而是删除它的左子树中值最大的那个节点,并用这个值代替原先应被删除的那个节点的
值。
?? ?17.4.3 在二叉树搜索树中查找
?? ?由于二叉搜索树的有序性,因此在树中查找一个特定的值是非常容易的。下面是它的算法:
?? ?如果树为空:
?? ??? ?这个值不存在于树中
?? ?否则:
?? ??? ?如果这个值和根节点的值相等:
?? ??? ??? ?成功找到这个值
?? ??? ?否则:
?? ??? ??? ?如果这个值小于根节点的值:
?? ??? ??? ??? ?查找左子树
?? ??? ??? ?否则:
?? ??? ??? ??? ?查找右子树
?? ?这个递归算法也属于尾部递归,所以采用迭代方案失效效率更高。
?? ?当值被找到是该做些什么呢?这取决于用户的需要。有时,用户只需要确定这个值是否存在于数中。这是,返回一个真/假值就足够了。如果数据是一个由一个关键字字段标识的结构,用户需要访问这个查找到的结构的非关键值成员,这就要求函数返回一个指向该结构的指针。
?? ?17.4.4 树的遍历
?? ?与堆栈和队列不同,树并未限制用户只能访问一个值。因此数具有另一个基本操作---遍历(traversal)。当检查一棵树的所有节点时,就是在遍历这棵树。遍历数的节点有几种不同的次序,最常用的是前序(pre-order)、中序(in-order)、后序(post-order)和层次遍历(breadth-first)。所有类型的遍历都是从树的根节点或希望开始遍历的子树的根节点开始。前序遍历检查节点的值,然后递归地遍历左子树和右子树。中序遍历首先遍历左子树,然后检查当前节点当前节点的值,最后遍历右子树。后序遍历首先遍历左右子树,然后检查当前节点的值。 最后,层次遍历逐层检查树的节点。首先处理根节点,接着是它的孩子,再接着是它的孙子,一次类推。
?? ?前3种遍历方法可以很容易地使用递归来实现,最后这种层次遍历要采用一种使用队列的迭代算法。?
?? ?17.4.5 二叉搜索树接口
?? ?程序17.7的接口提供了用于把值插入到一棵二叉搜索树的函数的原型。它同时包含了一个find函数,与查找树中某个特定的值,它的返回值是一个指向找到的值的指针。它只定义了一个遍历函数,因为其余遍历函数的接口只是名字不同而已。
?? ?/*
?? ?**二叉搜索树模块的接口。?
?? ?*/
?? ?#define TREE_TYPE int /*树的值类型。*/
?? ?
?? ?/*
?? ?**insert
?? ?**向树添加一个新值。参数是需要被添加的值,它必须原先不存在于树中。
?? ?*/
?? ?void insert( TREE_TYPE value );
?? ?
?? ?/*
?? ?**find
?? ?**查找一个特定值,这个值作为第1个参数传递给函数。
?? ?*/
?? ?TREE_TYPE *find( TREE_TYPE value );
?? ?
?? ?/*
?? ?**pre_order_traverse
?? ?**执行树的前序遍历。它的参数是一个回调函数指针,它所指向的函数将在树中处理每个节点时被调用,节点的值
?? ?**作为参数传递给这个函数。
?? ?*/?
?? ?void pre_order_traverse( void (*callback)( TREE_TYPE value ) );
程序17.7 二叉搜索树结构?? ?tree.h
?? ?17.4.6 实现二叉搜索树
?? ?尽管树的链式实现是最为常见的,但将二叉搜索树存储于数组中也是完全可能的。当然,数组的固定长度限制了可以插入到树中的元素的数量。如果使用动态数组,当原先的数组溢出时,就可以创建一个更大的空间并把值复制给它。
?? ?1.数组形式的二叉搜索树
?? ?用数组表示树的关键是使用下标来寻找某个特定值的双亲和孩子。规则很简单:
?? ?节点N的双亲是节点N/2。
?? ?节点N的左孩子是节点2N。
?? ?节点N的右孩子是节点2N+1。
?? ?双亲节点的公式是成立的,因为整除操作符将截去小数部分。
?? ?警告:
?? ?这里有个小问题。这些规定假定树的根节点是第1个节点,但C的数组下标从0开始。最容易的解决方案是忽略数组的第1个元素。如果元素非常大,这种方法将浪费很多空间,如果这样,可以使用基于零下标数组的另一套规则:
?? ?节点N的双亲结点是节点(N+1)/2-1。
?? ?节点N的左孩子节点是节点2N+1。
?? ?节点N的右孩子节点是节点2N+2。?
?? ?程序17.8是一个由静态数组实现的二叉搜索树。这个实现方法有几个有趣之处。它使用第1种更简单的规则来确定孩子节点,这样数组声明的长度比宣称的长度大1,它的第1个元素被忽略。它定义了一些函数来访问一个节点的左右孩子。尽管计算很简单,但这些函数名还是让使用这些函数的代码看上去更清晰。这些函数同时简化了“修改模块以便使用其他规则”的任务。?
?? ?这种实现方式使用0这个值提示一个节点未被使用。如果0是一个合法的数据值,那就必须另外挑选一个不同的值,而且数组元素必须进行动态初始化。另一个技巧是使用一个比较数组,它的元素是布尔类型,用于提示哪个节点被使用。
?? ?数组形式的树的问题在于数组空间常常利用得不够充分。空间之所以被浪费,是因为新值必须插入到树中特定的位置,无法随便放置到数组中的空位置。
?? ?为了说明这个情况,假定我们使用一个拥有100个元素的数组来容纳一棵树。如果值1,2,3,4,5,6和7以这个次序插入,它们将分别存储在数组中1,2,4,8,16,32和64的位置。但现在值8不能被插入,因为7的右孩子将存储于位置128,数组的长度没有那么长。这个问题会不会实际发生取决于值插入的顺序。如果相同的值以4,2,1,3,6,5和7的顺序插入,它们将占据数据1~7的位置,这样插入8这个值便毫无困难。
?? ?使用动态分配的数组,当需要更多空间时可以对数组进行重新分配。但是,对于一棵不平衡的树,这个技巧并不是一个好的解决方案,因为每次的新插入都将导致数组的大小扩大一倍,这样可用于动态分配的内存很快便会耗尽。一个更好的方法是使用链式二叉树而不是数组。
? ? /*
?? ?**一个使用静态数组实现的二叉树搜索树。数组的长度只能通过修改#define定义
?? ?**并对模块进行重新编译来实现。?
?? ?*/?
?? ?#include "tree.h"
?? ?#include <stdio.h>
?? ?#include <assert.h>
?? ?
?? ?#define TREE_SIZE 100 /*Max # of values in the trees*/
?? ?#define ARRAY_SIZE ( TREE_SIZE + 1 )
?? ?
?? ?/*
?? ?**用于存储树的所有结点的数组。?
?? ?*/
?? ?static TREE_TYPE tree[ ARRAY_SIZE ];
?? ?
?? ?/*
?? ?**left_child
?? ?**计算一个节点左孩子的下标。?
?? ?*/
?? ?static int?
?? ?left_child( int current ){
?? ??? ?return current * 2;
?? ?}?
?? ?
?? ?/*
?? ?**right_child
?? ?**计算一个节点右孩子的下标。?
?? ?*/
?? ?static int?
?? ?right_child( int current ){
?? ??? ?return current * 2 + 1;
?? ?}?
?? ??
?? ?/*
?? ?**insert
?? ?*/
?? ?void?
?? ?insert( TREE_TYPE value ){
?? ??? ?int current;
?? ??? ?
?? ??? ?/*
?? ??? ?**确保值为非零,因为零用于提示一个未使用的节点。
?? ??? ?*/
?? ??? ?assert( value != 0 );
?? ??? ?
?? ??? ?/*
?? ??? ?**从根节点开始
?? ??? ?*/
?? ??? ?current = 1;
?? ??? ?
?? ??? ?/*
?? ??? ?**从合适的子树开始,直到到达一个叶节点。
?? ??? ?*/
?? ??? ?while( tree[ current ] != 0 ){
?? ??? ??? ?/*
?? ??? ??? ?**根据情况,进入叶节点或右子树(确信未出现重复的值)
?? ??? ??? ?*/
?? ??? ??? ?if( value < tree[ current ] ){
?? ??? ??? ??? ?current = left_child( current );
?? ??? ??? ?}else{
?? ??? ??? ??? ?assert( value != tree[ current ] );
?? ??? ??? ??? ?current = right_child( current );
?? ??? ??? ?}
?? ??? ??? ?assert( current < ARRAY_SIZE );
?? ??? ?}
?? ??? ?
?? ??? ?tree[ current ] = value;?
?? ?}?
?? ?
?? ?/*
?? ?**find
?? ?*/
?? ?TREE_TYPE *
?? ?find( TREE_TYPE value ){
?? ??? ?int current;
?? ??? ?
?? ??? ?/*
?? ??? ?**从根节点开始。直到找到那个值,进入合适的子树。?
?? ??? ?*/
?? ??? ?current = 1;
?? ??? ?while( current < ARRAY_SIZE && tree[ current ] != value ){
?? ??? ??? ?/*
?? ??? ??? ?**根据情况,进入左子树或右子树。?
?? ??? ??? ?*/
?? ??? ??? ?if( value < tree[ current ] ){
?? ??? ??? ??? ?current = left_child( current );
?? ??? ??? ?}else{
?? ??? ??? ??? ?current = right_child( current );
?? ??? ??? ?}
?? ??? ?}?
?? ??? ?if( current < ARRAY_SIZE ){
?? ??? ??? ?return tree + current;?
?? ??? ?}else{
?? ??? ??? ?return 0;
?? ??? ?}
?? ?}
?? ?
?? ?/*
?? ?**do_pre_order_traverse
?? ?**执行一层前序遍历,这个帮助函数用于保存当前正在处理的节点的信息。
?? ?**它并不是用户接口的一部分。
?? ?*/
?? ?static void
?? ?do_pre_order_traverse( int current, void (*callback)( TREE_TYPE value ) ){
?? ??? ?if( current < ARRAY_SIZE && tree[ current ] != 0 ){
?? ??? ??? ?callback( tree[ current ] );
?? ??? ??? ?do_pre_order_traverse( left_child( current ), callback );
?? ??? ??? ?do_pre_order_traverse( right_child( current ), callback );?
?? ??? ?}
?? ?}
?? ?
?? ?/*
?? ?**pre_order_traverses
?? ?*/
?? ?void
?? ?pre_order_traverse( void (*callback)( TREE_TYPE value ) ){
?? ??? ?do_pre_order_traverse( 1, callback );
?? ?}?
程序17.8 用静态数组实现二叉搜索树?? ?a_tree.c
/*
**tree.h
**二叉搜索树模块的接口。?
*/
#define TREE_TYPE int /*树的值类型。*/
/*
**print?
**打印数组中的某个值。?
*/
void print( TREE_TYPE value );
/*
**insert
**向树添加一个新值。参数是需要被添加的值,它必须原先不存在于树中。
*/
void insert( TREE_TYPE value );
/*
**find
**查找一个特定值,这个值作为第1个参数传递给函数。
*/
TREE_TYPE *find( TREE_TYPE value );
/*
**pre_order_traverse
**执行树的前序遍历。它的参数是一个回调函数指针,它所指向的函数将在树中处理每个节点时被调用,节点的值
**作为参数传递给这个函数。
*/?
void pre_order_traverse( void (*callback)( TREE_TYPE value ) );
/*
**tree_2.cpp
**一个使用静态数组实现的二叉树搜索树。数组的长度只能通过修改#define定义
**并对模块进行重新编译来实现。?
*/?
#include "tree.h"
#include <stdio.h>
#include <assert.h>
#define TREE_SIZE 100 /*Max # of values in the trees*/
#define ARRAY_SIZE ( TREE_SIZE + 1 )
/*
**用于存储树的所有结点的数组。?
*/
static TREE_TYPE tree[ ARRAY_SIZE ];
/*
**left_child
**计算一个节点左孩子的下标。?
*/
static int?
left_child( int current ){
?? ?return current * 2;
}?
/*
**right_child
**计算一个节点右孩子的下标。?
*/
static int?
right_child( int current ){
?? ?return current * 2 + 1;
}?
?
/*
**print?
**打印数组中的某个值。?
*/
void print( TREE_TYPE value ){
?? ?printf( "%d ", value );?? ?
}?
/*
**insert
*/
void?
insert( TREE_TYPE value ){
?? ?int current;
?? ?
?? ?/*
?? ?**确保值为非零,因为零用于提示一个未使用的节点。
?? ?*/
?? ?assert( value != 0 );
?? ?
?? ?/*
?? ?**从根节点开始
?? ?*/
?? ?current = 1;
?? ?
?? ?/*
?? ?**从合适的子树开始,直到到达一个叶节点。
?? ?*/
?? ?while( tree[ current ] != 0 ){
?? ??? ?/*
?? ??? ?**根据情况,进入叶节点或右子树(确信未出现重复的值)
?? ??? ?*/
?? ??? ?if( value < tree[ current ] ){
?? ??? ??? ?current = left_child( current );
?? ??? ?}else{
?? ??? ??? ?assert( value != tree[ current ] );
?? ??? ??? ?current = right_child( current );
?? ??? ?}
?? ??? ?assert( current < ARRAY_SIZE );
?? ?}
?? ?
?? ?tree[ current ] = value;?
}?
/*
**find
*/
TREE_TYPE *
find( TREE_TYPE value ){
?? ?int current;
?? ?
?? ?/*
?? ?**从根节点开始。直到找到那个值,进入合适的子树。?
?? ?*/
?? ?current = 1;
?? ?while( current < ARRAY_SIZE && tree[ current ] != value ){
?? ??? ?/*
?? ??? ?**根据情况,进入左子树或右子树。?
?? ??? ?*/
?? ??? ?if( value < tree[ current ] ){
?? ??? ??? ?current = left_child( current );
?? ??? ?}else{
?? ??? ??? ?current = right_child( current );
?? ??? ?}
?? ?}?
?? ?if( current < ARRAY_SIZE ){
?? ??? ?return tree + current;?
?? ?}else{
?? ??? ?return 0;
?? ?}
}
/*
**do_pre_order_traverse
**执行一层前序遍历,这个帮助函数用于保存当前正在处理的节点的信息。
**它并不是用户接口的一部分。
*/
static void
do_pre_order_traverse( int current, void (*callback)( TREE_TYPE value ) ){
?? ?if( current < ARRAY_SIZE && tree[ current ] != 0 ){
?? ??? ?callback( tree[ current ] );
?? ??? ?do_pre_order_traverse( left_child( current ), callback );
?? ??? ?do_pre_order_traverse( right_child( current ), callback );?
?? ?}
}
/*
**pre_order_traverses
*/
void
pre_order_traverse( void (*callback)( TREE_TYPE value ) ){
?? ?do_pre_order_traverse( 1, callback );
}?
/*
tree_test.cpp
*/
#include <stdio.h>
#include <stdlib.h>
#include "tree.h"
int main( void ){
?? ?TREE_TYPE values[] = { 54, 36, 72, 22, 41, 61, 80, 16, 25, 40, 51, 73 };
?? ?int len;
?? ?int i;
?? ?
?? ?len = sizeof(values) / sizeof(*values);
?? ?for( i = 0; i < len; ++i ){
?? ??? ?insert( values[i] );
?? ?}
?? ?
?? ?printf( "the sequence of preorder traversal:\n" );
?? ?pre_order_traverse( print );
?? ?printf( "\n" );
?? ?
?? ?return EXIT_SUCCESS;
}
/* 输出:
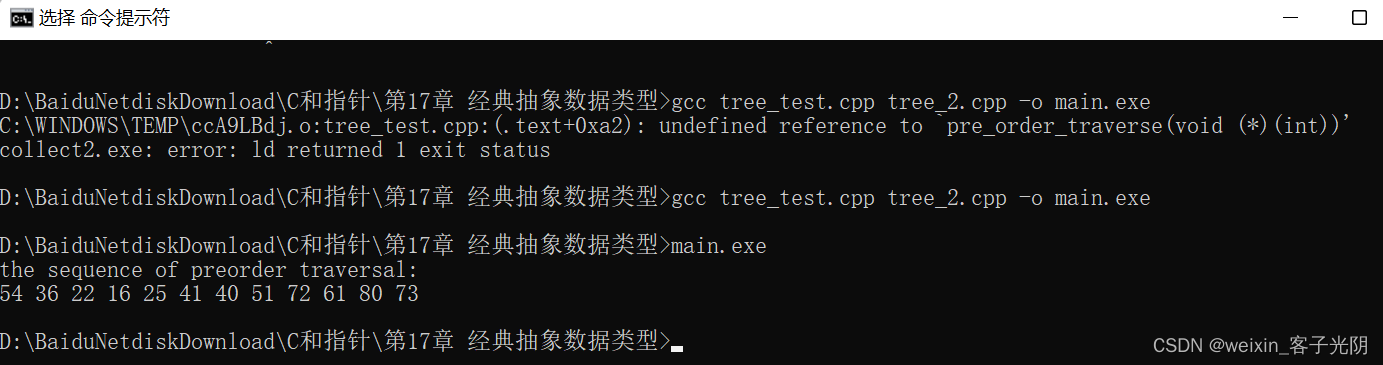
*/?
?? ?2.链式二叉搜索树
?? ?队列的链式表示消除了数组空间利用不充分的问题,这是通过为每个新值动态分配内存并把这些结构链接到树中实现的。因此,不存在未使用的内存。
?? ?程序17.9是二叉树搜索树的链式实现方法。请将它和17.8的数组实现方法进行比较。由于树中的每个节点必须指向它的左右孩子,因此节点用一个结构来容纳值和两个指针。数组由一个指向树根节点的指针代替。这个指针最初为NULL,表示此时为一棵空树。
?? ?insert函数使用两个指针(这里使用的技巧与第12章的函数中把值插入到一个有序的单链表的技巧相同。如果沿着从根到叶的路径观察插入发生的位置,就会发现它本质上就是一个单链表。)。第1个指针用于检查树中的节点,寻找新值插入的合适位置。第2个指针指向另一个节点,后者的link字段指向当前正在检查的节点。当到达一个叶节点时,这个指针必须进行修改以插入新节点。这个函数自上而下,根据新值与当前节点值的比较结果选择正确进入左子树或右子树,直到到达叶节点。然后,创建一个新节点并链接到树中。这个迭代算法在插入第1个节点时也能正确处理,不会造成特殊情况。?
?? ?3.树接口的变型
?? ?find函数只用于验证值是否存在于树中。返回一个指向找到元素的指针并无大用,因为调用程序已经知道这个值:它就是传递给函数的参数嘛!
?? ?假定树中的元素实际上是一个结构,它包括一个关键字和一些数据。现在可以修改find函数,使它更加实用。通过它的关键字查找一个特定的节点并返回一个指向该结构的指针,可以向用户提供更多的信息---与这个关键值相关联的数据。但是,为了取得这个结果,find函数必须设法只比较每个节点元素的关键值部分。解决办法是编写一个函数执行这个比较,并把一个指向该函数的指针传递给find函数,就像在qsort函数中所采用的方法一样。
?? ?有时候用户可能要求自己遍历整棵树,例如,计算每个节点的孩子数量。因此,TreeNode结构和指向树根节点的指针都必须声明为公用,以便用户遍历该树。最安全的方式是通过函数向用户提供根指针,这样可以防止用于自行修改根指针,从而导致丢失整棵树。
?? ?/*
?? ?**一个使用动态分配的链式结构实现的二叉搜索树。
?? ?*/
?? ?#include "tree.h"
?? ?#include <assert.h>
?? ?#include <stdio.h>
?? ?#include <malloc.h>
?? ?
?? ?/*
?? ?**TreeNode结构包含了值和两个指向某个树节点的指针。
?? ?*/
?? ?typedef struct TREE_NODE{
?? ??? ?TREE_TYPE value;
?? ??? ?struct TREE_NODE *left;
?? ??? ?struct TREE_NODE *right;
?? ?} TreeNode;
?? ?
?? ?/*
?? ?**指向树根节点的指针?
?? ?*/?
?? ?static TreeNode *tree;
?? ?
?? ?/*
?? ?**insert
?? ?*/
?? ?void?
?? ?insert( TREE_TYPE value ){
?? ??? ?TreeNode *current;
?? ??? ?TreeNode **link;
?? ??? ?
?? ??? ?/*
?? ??? ?**从根节点开始。?
?? ??? ?*/?
?? ??? ?link = &tree;
?? ??? ?/*
?? ??? ?**持续查找值,进入合适的子树。
?? ??? ?*/
?? ??? ?while( (current = *link) != NULL ){
?? ??? ??? ?/*
?? ??? ??? ?**根据情况,进入左子树或右子树(确认没有出现重复的值)
?? ??? ??? ?*/
?? ??? ??? ?if( value < current->value ){
?? ??? ??? ??? ?link = ¤t->left;
?? ??? ??? ?}else{
?? ??? ??? ??? ?assert( value != current->value );
?? ??? ??? ??? ?link = ¤t->right;
?? ??? ??? ?}
?? ??? ?}
?? ??? ?
?? ??? ?/*
?? ??? ?**分配一个新节点,使适当节点的link字段指向它。
?? ??? ?*/
?? ??? ?current = malloc( sizeof( TreeNode ) );
?? ??? ?assert( current != NULL );
?? ??? ?current->value = value;
?? ??? ?current->left = NULL;
?? ??? ?current->right = NULL;
?? ??? ?*link = current;?
?? ?}?
?? ?
?? ?/*
?? ?**find
?? ?*/
?? ?TREE_TYPE *
?? ?find( TREE_TYPE value ){
?? ??? ?TreeNode *current;
?? ??? ?
?? ??? ?/*
?? ??? ?**从根节点开始,直到找到这个值,进入合适的子树。
?? ??? ?*/
?? ??? ?current = tree;
?? ??? ?
?? ??? ?while( current != NULL && current->value != value ){
?? ??? ??? ?/*
?? ??? ??? ?**根据情况,进入左子树或右子树。
?? ??? ??? ?*/
?? ??? ??? ?if( value < current->value ){
?? ??? ??? ??? ?current = current->left;?
?? ??? ??? ?}else{
?? ??? ??? ??? ?current = current->right;
?? ??? ??? ?}
?? ??? ?}
?? ??? ?if( current != NULL ){
?? ??? ??? ?return ¤t->value;
?? ??? ?}else{
?? ??? ??? ?return NULL;
?? ??? ?}
?? ?}
?? ?
?? ?/*
?? ?**do_pre_order_traverse
?? ?**执行一层前序遍历。这个帮助函数用于保存当前正在处理的节点的信息。
?? ?**这个函数并不是用户接口的一部分。
?? ?*/
?? ?static void?
?? ?do_pre_order_traverse( TreeNode *current, void (*callback)( TREE_TYPE value ) ){
?? ??? ?if( current != NULL ){
?? ??? ??? ?callback( current->value );
?? ??? ??? ?do_pre_order_traverse( current->left, callback );
?? ??? ??? ?do_pre_order_traverse( current->right, callback );
?? ??? ?}
?? ?}?
?? ?
?? ?/*
?? ?**pre_order_traverse
?? ?*/
?? ?void
?? ?pre_order_traverse( void (*callback)( TREE_TYPE value ) ){
?? ??? ?do_pre_order_traverse( tree, callback );
?? ?}?
程序17.9 链式二叉搜索树?? ?l_tree.c
/* tree.h跟上面我测试的第一个一模一样。因此这里省略。*/
/*
dynamic_tree_test.cpp
*/
#include <stdio.h>
#include <stdlib.h>
#include "tree.h"
int main( void ){
?? ?TREE_TYPE values[] = { 54, 36, 72, 22, 41, 61, 80, 16, 25, 40, 51, 73 };
?? ?int len;
?? ?int i;
?? ?
?? ?len = sizeof(values) / sizeof(*values);
?? ?for( i = 0; i < len; ++i ){
?? ??? ?insert( values[i] );
?? ?}
?? ?
?? ?printf( "the sequence of preorder traversal:\n" );
?? ?pre_order_traverse( print );
?? ?printf( "\n" );
?? ?
?? ?return EXIT_SUCCESS;
}
/*
**tree_3.cpp
**一个使用动态分配的链式结构实现的二叉搜索树。
*/
#include "tree.h"
#include <assert.h>
#include <stdio.h>
#include <malloc.h>
/*
**TreeNode结构包含了值和两个指向某个树节点的指针。
*/
typedef struct TREE_NODE{
?? ?TREE_TYPE value;
?? ?struct TREE_NODE *left;
?? ?struct TREE_NODE *right;
} TreeNode;
/*
**指向树根节点的指针?
*/?
static TreeNode *tree;
/*
**print?
**打印数组中的某个值。?
*/
void print( TREE_TYPE value ){
?? ?printf( "%d ", value );?? ?
}?
/*
**insert
*/
void?
insert( TREE_TYPE value ){
?? ?TreeNode *current;
?? ?TreeNode **link;
?? ?
?? ?/*
?? ?**从根节点开始。?
?? ?*/?
?? ?link = &tree;
?? ?/*
?? ?**持续查找值,进入合适的子树。
?? ?*/
?? ?while( (current = *link) != NULL ){
?? ??? ?/*
?? ??? ?**根据情况,进入左子树或右子树(确认没有出现重复的值)
?? ??? ?*/
?? ??? ?if( value < current->value ){
?? ??? ??? ?link = ¤t->left;
?? ??? ?}else{
?? ??? ??? ?assert( value != current->value );
?? ??? ??? ?link = ¤t->right;
?? ??? ?}
?? ?}
?? ?
?? ?/*
?? ?**分配一个新节点,使适当节点的link字段指向它。
?? ?*/
?? ?current = (TreeNode *)malloc( sizeof( TreeNode ) );
?? ?assert( current != NULL );
?? ?current->value = value;
?? ?current->left = NULL;
?? ?current->right = NULL;
?? ?*link = current;?
}?
/*
**find
*/
TREE_TYPE *
find( TREE_TYPE value ){
?? ?TreeNode *current;
?? ?
?? ?/*
?? ?**从根节点开始,直到找到这个值,进入合适的子树。
?? ?*/
?? ?current = tree;
?? ?
?? ?while( current != NULL && current->value != value ){
?? ??? ?/*
?? ??? ?**根据情况,进入左子树或右子树。
?? ??? ?*/
?? ??? ?if( value < current->value ){
?? ??? ??? ?current = current->left;?
?? ??? ?}else{
?? ??? ??? ?current = current->right;
?? ??? ?}
?? ?}
?? ?if( current != NULL ){
?? ??? ?return ¤t->value;
?? ?}else{
?? ??? ?return NULL;
?? ?}
}
/*
**do_pre_order_traverse
**执行一层前序遍历。这个帮助函数用于保存当前正在处理的节点的信息。
**这个函数并不是用户接口的一部分。
*/
static void?
do_pre_order_traverse( TreeNode *current, void (*callback)( TREE_TYPE value ) ){
?? ?if( current != NULL ){
?? ??? ?callback( current->value );
?? ??? ?do_pre_order_traverse( current->left, callback );
?? ??? ?do_pre_order_traverse( current->right, callback );
?? ?}
}?
/*
**pre_order_traverse
*/
void
pre_order_traverse( void (*callback)( TREE_TYPE value ) ){
?? ?do_pre_order_traverse( tree, callback );
}?
/* 输出:

*/?
?? ?让每个树节点拥有一个指向它的双亲结点的指针往往很有用。用户可以利用这个双亲结点指针在树中上下移动。这种更为开放的树的find函数可以返回一个指向这个树节点的指针(而不是节点值),这就允许用户利用这个指针执行其他形式的遍历。
?? ?程序的最后一个可供改进之处是用一个destroy_tree函数释放所有分配给这棵树的内存。