假设有一个数组a[N] N<=20
能不能从数组a中任选M个元素(M<=N),使得其和为K。
解题思路:穷举法
利用穷举法,将所有的情况进行运算,直到找到该子数组为止。
我们利用二进制来表示数组中的数据是否在子数组中,其中0表示不在,1表示在。
例如数组a为{21, 1, 35, 15, 32, 12, 5, 7},我们需要找到三个数之和为79。
则用二进制进行表示则为00110100(这里要注意的是,二进制表示与数组的顺序是反过来的,则00000001,表示的是a[0],而不是a[7])。
同时,我们对该二进制数据进行右移运算,并与1进行与运算,当结果为1的时候,我们将数据进行相加,如果与K相等并且二进制表示中的1的个数与M相等,则数组a中有M个元素其和为K。
针对于这个算法,我们需要利用到两个for循环,第一个for循环用来对各种情况进行遍历,第二个for循环用来对第一个循环中的情况进行运算,即:
for (int i = 0; i < (1 << N); i++) // i用于统计各种情况
{
for (int j = 0; j < N; j++)
{
……
}
}
对于第二个循环中,我们应该如何去针对于第一个循环中的情况进行运算呢?
例如,数组a为{21, 1, 35, 15, 32, 12, 5, 7},我们需要找到三个数之和为79,而这中情况用二进制进行表示则为00110100
在第二个循环中,当j=2时,该二进制数进行右移两位,结果为00001101,我们再对它与1进行与运算,结果为1
所以,我们找到了我们需要的第一个数,即为a[2],以此类推,我们就会找到剩下的两个数
所以第二个循环的j表示的是右移的位数,当与1与运算的结果为1时,我们才进行计算,为0时不计算,所以我们还需要一个条件语句进行判断即:
for (int i = 0; i < (1 << N); i++) // i用于统计各种情况
{
for (int j = 0; j < N; j++)
{
if ((i >> j) & 1) //通过与1进行与运算,来对所有情况进行求和
{
}
}
if (sum == K && count == M)//打印结果
{
……
}
}
最后我们的最终代码应该为
#include <stdio.h>
#define N 20
int main()
{
int sum; //用来计算M个元素之和
int count; //用来统计已经相加的元素个数,用于判断是否和M相等
int flag = 0; //用来标记结果,1表示数组a中有M个元素其和为K,0表示没有
int M, K;
int a[N] = {21, 1, 35, 15, 32, 12, 5, 7};
scanf("%d %d", &M, &K);
for (int i = 0; i < (1 << N); i++) // i用于统计各种情况
{
sum = 0;
count = 0; //每结束一次循环,sum、count都需要重新置零
for (int j = 0; j < N; j++)
{
if ((i >> j) & 1) //通过与1进行与运算,来对所有情况进行求和
{
sum += a[j];
count++;
}
}
if (sum == K && count == M)//打印结果
{
flag = 1;
count = 0;
printf("数组a中存在%d个元素其和为%d\n", M, K);
for (int j = 0; j < N; j++)
{
if ((i >> j) & 1)
{
count++;
if (count == M)
printf("%d", a[j]);
else
printf("%d+", a[j]);
}
}
printf("=%d\n", K);
break;
}
}
if (flag == 0)//如果数组中不存在M个元素其和为K
{
printf("数组a中不存在%d个元素其和为%d\n", M, K);
}
}
我们对代码进行编译与运行,结果为:
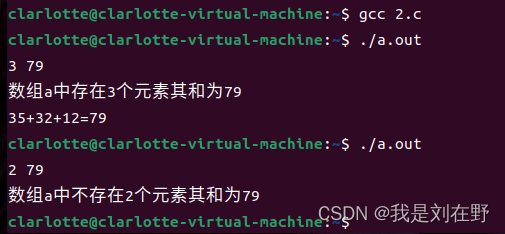
如有错误,请批评指出,希望各位大佬指点