二叉树非递归先序、中序、后序遍历过程详解及C++详细实现
前置知识点如下:
树与二叉树的定义,性质。二叉树的顺序存储结构,链式存储结构。
二叉树的先序,中序,后序,层序遍历;由遍历序列构造二叉树详解及C++详细实现
如下图所示,用带箭头的虚线表示了这3种遍历算法的递归执行过程。其中,向下的箭头表示更深 一层的递归调用,向上的箭头表示从递归调用退出返回。
虚线旁的三角形、圆形和方形内的字符分别表示在先序、中序和后序遍历的过程中访问结点时输出的信息。
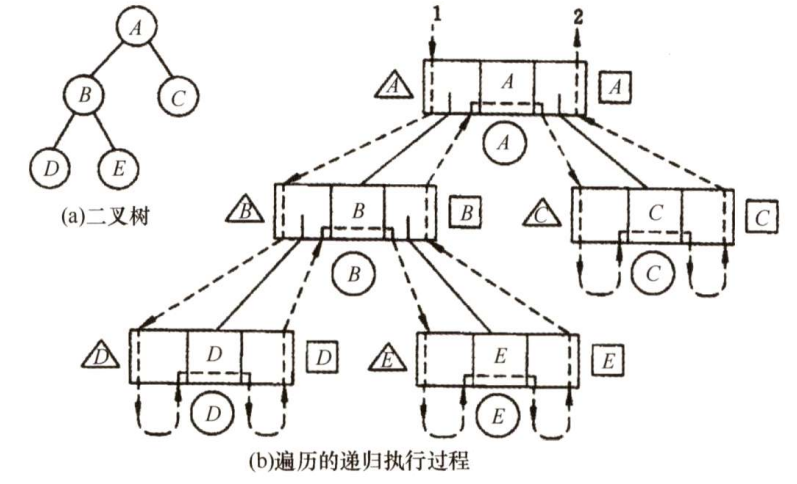
例如,由于中序遍历中访问结点是在遍历左子树之后、遍历右子树之前进行的,则带圆形的字符标在向左递归返回和向右递归调用之间
如上图所示,只要沿虚线从1出发到2结束,将沿途所见的三角形(或圆形或方形)内的字符记下,便得到遍历二叉树的先序(或中序或后序)序列
沿虚线游走:
- 输出三角形,得到先序序列 A B D E C {\rm ABDEC} ABDEC 。
- 输出圆形,得到中序序列 D B E A C {\rm DBEAC} DBEAC 。
- 输出方形,得到后序序列 D E B C A {\rm DEBCA} DEBCA 。
非递归中序遍历
借助栈,我们来分析中序遍历的访问过程:
1)沿着根的左孩子,依次入栈,直到左孩子为空,说明已找到可以输出的结点,此时栈内元素依次为 A B D {\rm ABD} ABD 。
2)栈顶元素出栈并访问:若其右孩子为空,继续执行步骤2,若其右孩子不空,将右子树转执行步骤1。
如上图二叉树为例,分析其非递归中序遍历过程:
栈顶 D {\rm D} D 出栈并访问,它是中序序列的第一个结点; D {\rm D} D 的右孩子为空,栈顶 B {\rm B} B 出栈并访问; B {\rm B} B 右孩子不空,将其右孩子 E {\rm E} E 入栈, E {\rm E} E 左孩子为空,栈顶 E {\rm E} E 出栈并访问; E {\rm E} E 右孩子为空,栈顶 A {\rm A} A 出栈并访问; A {\rm A} A 右孩子不空,将其右孩子 C {\rm C} C 入栈, C {\rm C} C 左孩子为空,栈顶 C {\rm C} C 出栈并访问。由此得到中序序列 D B E A C {\rm DBEAC} DBEAC 。
根据分析可以写出中序遍历的非递归算法如下:
#include <iostream>
#include "stack"
using namespace std;
template<typename T>
struct BiTNode {
T data; //数据域
BiTNode *lchild, *rchild; //左、右孩子指针
};
template<typename T>
class BiTree {
private:
BiTNode<T> *root; //根结点
//非递归中序遍历
void InOrder2(BiTNode<T> *biTNode) {
stack<BiTNode<T> *> s; //注意栈里面存的是地址
BiTNode<T> *p = root; //p是遍历指针
while (p || !s.empty()) { //栈不空或者指针p不空时,循环
if (p) {
s.push(p); //当前结点入栈
p = p->lchild; //左孩子不为空,一直向左走
} else {
p = s.top(); //栈顶元素出栈,访问栈顶元素
cout << p->data << "\t";
s.pop();
p = p->rchild; //向栈顶元素的右子树走
}
}
}
public:
//非递归中序遍历
void InOrder2() {
InOrder2(root);
}
}
非递归先序遍历
先序遍历和中序遍历的基本思想是类似的,只需把访问结点操作放在入栈操作的前面即可
先序遍历的非递归算法如下:
//非递归先序遍历
void PreOrder2(BiTNode<T> *biTNode) {
stack<BiTNode<T> *> s; //注意栈里面存的是地址
BiTNode<T> *p = root; //p是遍历指针
while (p || !s.empty()) { //栈不空或者指针p不空时,循环
if (p) {
cout << p->data << "\t"; //访问当前结点并入栈
s.push(p);
p = p->lchild; //左孩子不为空,一直向左走
} else {
p = s.top();
s.pop(); //栈顶元素出栈
p = p->rchild; //向栈顶元素的右子树走
}
}
}
非递归后序遍历
后序遍历的非递归实现是三种遍历方法中最难的。因为在后序遍历中,要保证左孩子和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点。
后序非递归遍历算法的思路分析:
从根结点开始,将其入栈,然后沿其左子树一直往下搜索,直到搜索到没有左孩子的结点,但是此时不能出栈并访问,因为如果其有右子树,还需按相同的规则对其右子树进行处理。直至上述操作进行不下去,若栈顶元素想要出栈被访问,要么右子树为空,要么右子树刚被访问完(此时左子树早已访问完),这样就保证了正确的访问顺序。

现在依然结合上图的二叉树来分析,后序非递归遍历的过程如下:
1)沿着根的左孩子,依次入栈,直到左孩子为空。此时栈内元素依次为
A
B
D
{\rm ABD}
ABD 。
2)读栈顶元素:若其右孩子不空且未被访问过,将右子树转执行步骤1,否则,栈顶元素出栈并访问。
栈顶
D
{\rm D}
D 的右孩子为空,出栈并访问,它是后序序列的第一个结点。
栈顶
B
{\rm B}
B 的右孩子不空且未被访问过,
E
{\rm E}
E 入栈。
栈顶
E
{\rm E}
E 的左右孩子均为空,出栈并访问。
栈顶
B
{\rm B}
B 的右孩子不空但已被访问,
B
{\rm B}
B 出栈并访问。
栈顶
A
{\rm A}
A 的右孩子不空且未被访问过,
C
{\rm C}
C 入栈。
栈顶
C
{\rm C}
C 的左右孩子均为空,出栈并访问。
栈顶
A
{\rm A}
A 的右孩子不空但已被访问,
A
{\rm A}
A 出栈并访问。
由此得到后序序列:
D
E
B
C
A
{\rm DEBCA}
DEBCA。
在上述思想的第2步中,必须分清返回时是从左子树返回的还是从右子树返回的,因此设定一个辅助指针r,指向最近访问过的结点,也可在结点中增加一个标志域,记录是否已被访问。
后序遍历的非递归算法如下:
//非递归后序遍历
void PostOrder2(BiTNode<T> *biTNode) {
stack<BiTNode<T> *> s; //注意栈里面存的是地址
BiTNode<T> *p = root; //p是遍历指针
BiTNode<T> *r = NULL; //记录最近访问过的结点
while (p || !s.empty()) {
if (p) {
s.push(p);
p = p->lchild; //一直走到最左边
} else {
p = s.top(); //拿到栈顶元素
if (p->rchild && p->rchild != r) //右子树存在并且未被访问过
p = p->rchild; //向右走一步
else {
p = s.top();
cout << p->data << "\t"; //访问栈顶元素并将其弹出
s.pop();
r = p; //记录最近访问过的结点
p = NULL; //以p为根结点的子树已经访问完了,置为空
}
}
}
}
注意:每次出栈访问完一个结点就相当于遍历完以该结点为根的子树,需将p置NULL
完整代码
非递归先序、中序、后序遍历完整代码以及测试代码如下:
二叉树构造算法详解点击此处
#include <iostream>
#include "stack"
using namespace std;
template<typename T>
struct BiTNode {
T data; //数据域
BiTNode *lchild, *rchild; //左、右孩子指针
};
template<typename T>
class BiTree {
private:
BiTNode<T> *root; //根结点
T *pre; //先序序列
T *in; //中序序列
int length; //二叉树中的结点个数
//构造二叉树
//当前先序序列区间为[preL, preR],中序序列区间为[inL, inR],返回根结点地址
BiTNode<T> *create(int preL, int preR, int inL, int inR) {
if (preL > preR)
return NULL; //先序序列长度小于等于0时,直接返回
BiTNode<T> *biTNode = new BiTNode<T>; //新建一个新的结点,用来存放当前二叉树的根结点
biTNode->data = pre[preL]; //新结点的数据域为根结点的值,根结点是当前先序序列区间的第1个结点
int k; //存储当前中序序列区间的根结点的索引
for (k = inL; k <= inR; k++)
if (in[k] == pre[preL]) //在中序序列中找到in[k] == pre[L]的结点
break;
int numLeft = k - inL; //左子树的结点个数
//左子树的先序区间为[preL+1,preL+numLeft],中序区间为[inL,k-1]
//返回左子树的根结点地址,赋值给root的左指针
biTNode->lchild = create(preL + 1, preL + numLeft, inL, k - 1);
//右子树的先序区间为[preL + numLeft + 1,preR],中序区间为[k+1,inR]
//返回右子树的根结点地址,赋值给root的右指针
biTNode->rchild = create(preL + numLeft + 1, preR, k + 1, inR);
return biTNode; //返回根结点地址
}
//非递归先序遍历
void PreOrder2(BiTNode<T> *biTNode) {
stack<BiTNode<T> *> s; //注意栈里面存的是地址
BiTNode<T> *p = root; //p是遍历指针
while (p || !s.empty()) { //栈不空或者指针p不空时,循环
if (p) {
cout << p->data << "\t"; //访问当前结点并入栈
s.push(p);
p = p->lchild; //左孩子不为空,一直向左走
} else {
p = s.top();
s.pop(); //栈顶元素出栈
p = p->rchild; //向栈顶元素的右子树走
}
}
}
//非递归中序遍历
void InOrder2(BiTNode<T> *biTNode) {
stack<BiTNode<T> *> s; //注意栈里面存的是地址
BiTNode<T> *p = root; //p是遍历指针
while (p || !s.empty()) { //栈不空或者指针p不空时,循环
if (p) {
s.push(p); //当前结点入栈
p = p->lchild; //左孩子不为空,一直向左走
} else {
p = s.top(); //栈顶元素出栈,访问栈顶元素
cout << p->data << "\t";
s.pop();
p = p->rchild; //向栈顶元素的右子树走
}
}
}
//非递归后序遍历
void PostOrder2(BiTNode<T> *biTNode) {
stack<BiTNode<T> *> s; //注意栈里面存的是地址
BiTNode<T> *p = root; //p是遍历指针
BiTNode<T> *r = NULL; //记录最近访问过的结点
while (p || !s.empty()) {
if (p) {
s.push(p);
p = p->lchild; //一直走到最左边
} else {
p = s.top(); //拿到栈顶元素
if (p->rchild && p->rchild != r) //右子树存在并且未被访问过
p = p->rchild; //向右走一步
else {
p = s.top();
cout << p->data << "\t"; //访问栈顶元素并将其弹出
s.pop();
r = p; //记录最近访问过的结点
p = NULL; //以p为根结点的子树已经访问完了,置为空
}
}
}
}
public:
//初始化先序序列,中序序列,然后根据这两个序列构造二叉树
BiTree(T *pre, T *in, int length) {
this->length = length;
this->pre = new T[length + 1];
this->in = new T[length + 1];
//初始化先序序列,中序序列
for (int i = 1; i <= length; i++) {
this->pre[i] = pre[i];
this->in[i] = in[i];
}
//构造二叉树
root = create(1, length, 1, length);
}
//非递归先序遍历
void PreOrder2() {
PreOrder2(root);
}
//非递归中序遍历
void InOrder2() {
InOrder2(root);
}
//非递归后序遍历
void PostOrder2() {
PostOrder2(root);
}
};
int main() {
char pre[] = {'#', 'A', 'B', 'D', 'E', 'C'};
char in[] = {'#', 'D', 'B', 'E', 'A', 'C'};
BiTree<char> biTree(pre, in, 5);
cout << "PreOrder:\t";
biTree.PreOrder2();
cout << endl;
cout << "InOrder:\t";
biTree.InOrder2();
cout << endl;
cout << "PostOrder:\t";
biTree.PostOrder2();
cout << endl;
return 0;
}
运行结果:
PreOrder: A B D E C
InOrder: D B E A C
PostOrder: D E B C A