文章目录
前言
本文主要了解一些前置后置++、- -的使用规则,先使用?怎么个先使用法;如果没有接收方,那这个先使用又是如何体现的;正整数的取模运算我们能理解,那么再深入思考一下,负数是怎么进行取模运算的呢?
接下来,我将与大家一起讨论以上问题。
一、++、- -先使用?
在了解之前,我们可能会看一点点汇编来进行理解;
1、赋初值与赋值的区别
首先,我们先回答一个问题,赋初值和赋值是否一样?
…
严谨上来说是不一样的,但是我们在日常的使用中经常经常把这两个概念给搞混淆,具体怎么个不一样呢?我们通过汇编的方式来理解一下;
int main()
{
int a = 10;//这叫赋初值
int b = 20;
b = a;//这叫赋值
return 0;
}
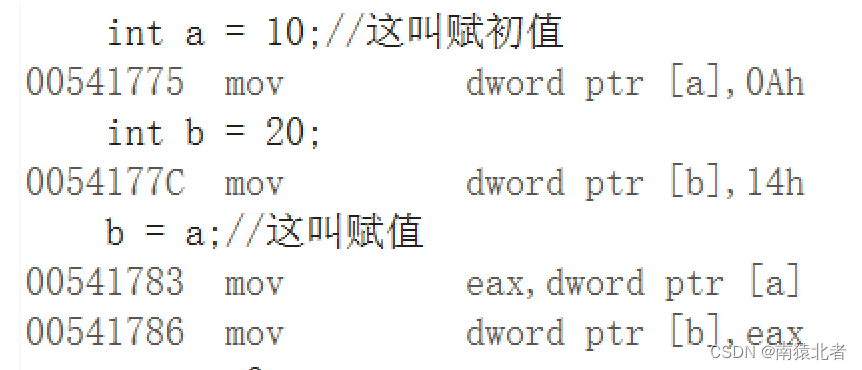
这便是这段代码对应的汇编片段;
接下来,我就为大家从汇编的角度,解释一下,为什么赋初值和赋值的不一样;

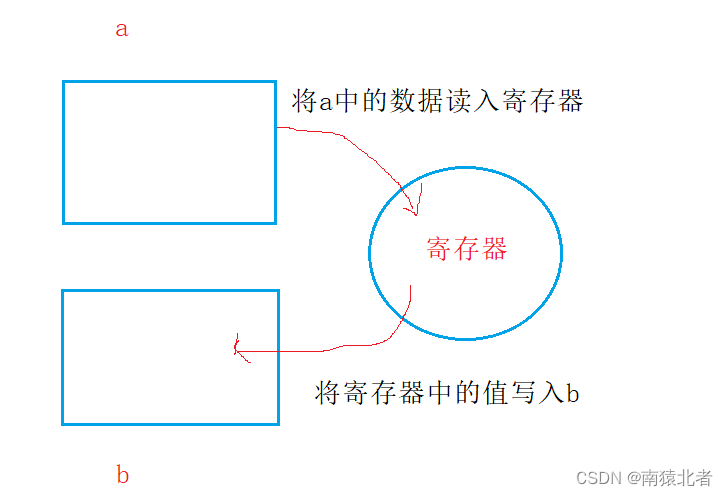
其实从汇编的角度,我们理解到赋初值的话是不需要经过寄存器的,直接往开辟好的空间里放数据,这也从侧面说明了赋初值其实完成了两件事:1、开辟空间。2、给空间里面赋值。
然后我们再来看一看赋值:通过汇编指令我们可以看出,1、赋值不需要开辟空间。2、赋值不能直接完成,必须通过寄存器完成;
以上就是赋初值与赋值的区别了;
总结一下:
赋值并不能直接完成,必须通过寄存器才能完成;而赋初值不需要寄存器,直接就能完成;
2、++、- -
接下来让我们回归主题;
测试代码:
int main()
{
int a = 4;
int b = 2;
b = a++;
return 0;
}
这段代码,大家一眼就看出来了b的值变为了4,a的值变为了5;
怎么变得?先使用后加加嘛,a的值先使用,也就是赋给b,然后再自增;就得到以上结果了;
这是粗略的理解,接下来我们再从汇编的角度理解一下有接收方的情况;

这是以上代码所对应的汇编;接下来我来解释一下;

(先自增,再使用的情况,也是同样的道理)

接下来我们来讨论一下,没有接收放的情况下,这个先使用(或后使用是如何体现的;)
测试代码:
int main()
{
int a = 1;
a++;
return 0;
}

与之对应的汇编语言;
从汇编语言我们可以看出,再没有接收方的情况下,先使用(或后使用的情况是不存在的,没有谁来接收,自然也就没有先使用(或后使用的汇编指令,直接自增完过后,再写回内存就行了)
同理++a也是同样的道理;
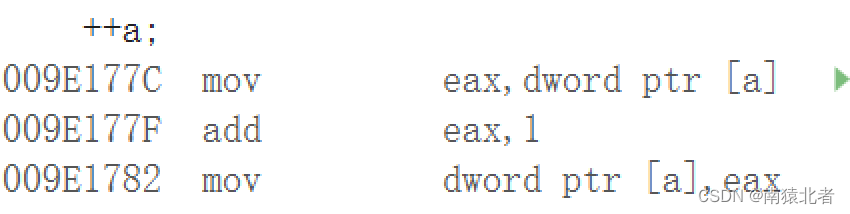
总体效果与a++是一样的;
总结一下:
对于前后置++、- -来说,如果有接受方的话,就会执行先使用(或后使用的操作),对于那种没有接收方的,就会直接对自己进行自增(或自减),不会进行多余的操作,同时这时候的前置++、- -和后置++、- -能到达相同的效果;
3、“经典”错误
大家先看一下,以下代码:
int main()
{
int a = 1;
int b = 1;
b = (++a) + (++a) + (++a);
printf("%d\n",b);
return 0;
}
大家可以猜一下,这个运行结果:
答案是这段代码无确定结果,在不同编译器下,运行结果不一样;
在VS2019中:

在Dev环境下:
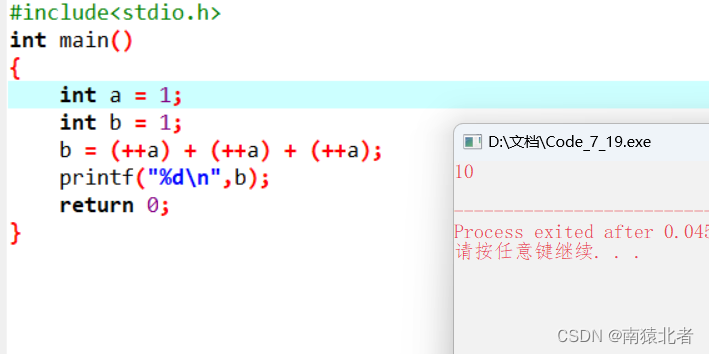
在手机上:

为什么会出现这种情况,接下来我们就从汇编的角度(VS2019环境下)来理解一下:

导致以上结果的原因,主要是由于,各个平台的编译器,对于以上的汇编代码解释方式不一样,(也可以认为是代码本身不够严谨,对于就算的途径不唯一),对于VS2019来说,他认为的是先将++执行完,在把a的值写回内存,在执行的+法运算;但是有的编译器,有可能就是先进行的1、2步骤,在写入内存,在读取到寄存器当中,在执行的3步骤,然后并未重新将a的值从新写入内存,然后,再进行相加运算,这就导致了,在内存中a的值,一直是上一次的值,而寄存器中的值是自增过后的值,但是并未重新写回内存,就会造成上次的值和刷新过后的值的混合使用,就会造成最终的运行结果不一样;
总结一下:
在我们日常学习和工作中,我们应当避免写出这种有歧义的代码,减少出bug的机率和成本;
二、负数取模?
在我们C语言的学习中。%操作符是我们经常用到的,用途也很广泛;
但是如果咱们足够留意的话,咱们会发现,咱们遇到的%运算,似乎都是针对正数来进行的;
对于负数的%运算我们似乎并不是那么了解;
那么接下来我们就来详细的了解一下;
1、取整方式
在正式进去主题之前,我们得先了解一下:取整的方式:
int a=3.14;
在C语言当中我们都知道,取整的方式就是,舍弃小数部分,直接取整数部分,比如上述代码,a=3;
那么是不是就只有这一种取整方式呢?
当然不是啦!世界都有多样性,何况C语言呢;
A、向0取整
大概意思,就是以下的意思:
示意图:
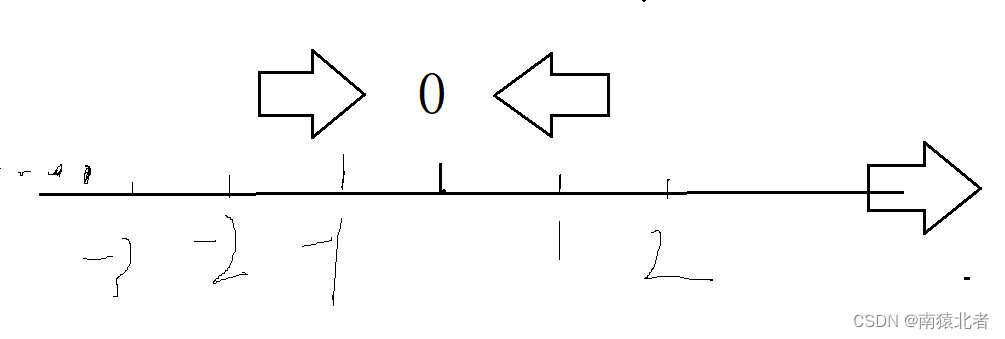
当我们对一个小数取整的时候,我们因该尽可能的向0的方向取整;
什么个意思呢?举个例子:
-3.79取整,就是-3;
-3.1取整,就是-3;
3.9取整,就是3;
现在大概能理解了吧;
这个取整方法,就要求我们取靠近0的,还要靠近我们的小数的的整数;😁😁😁
B、向负无穷取整
这个取整方法也很好理解:
示意图:
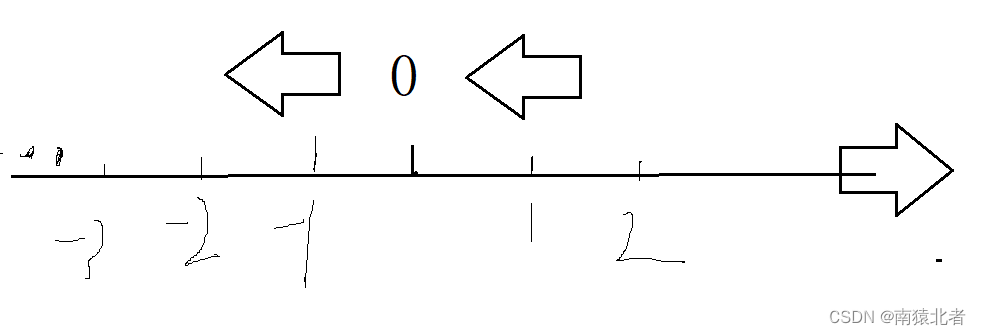
举个栗子:
-3.79取整,就是-4;
-3.1取整,就是-4;
3.9取整,就是3;
现在大概能理解了吧;
这个取整方法,就要求我们取靠近负无穷的,还要靠近我们的小数的的整数;😁😁😁
C、向正无穷取整
这个也很好理解:
示意图:
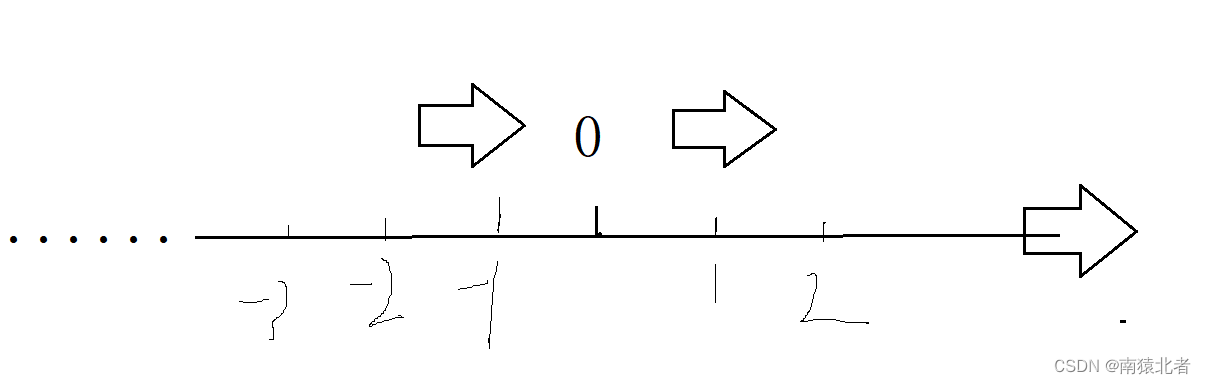
举个栗子:
-3.79取整,就是-3;
-3.1取整,就是-3;
3.9取整,就是4;
现在大概能理解了吧;
这个取整方法,就要求我们取靠近正无穷的,还要靠近我们的小数的的整数;😁😁😁
D、四舍五入取整
这应该是最能理解的了吧。😀😀😀
举个栗子:
-3.79取整,就是-4;
-3.1取整,就是-3;
3.9取整,就是4;
写个代码出来总体感受以下:
#include<math.h>
int main()
{
float a, b, c, d, e;
a = 1.0f;
b = 2.1f;
c = -1.3f;
d = -0.2f;
e = 3.76f;
printf("f_val\ttrunc\tfloor\tceil\tround\n");
printf("%.1f\t%.1f\t%.1f\t%.1f\t%.1f\n", a, trunc(a), floor(a), ceil(a), round(a));
printf("%.1f\t%.1f\t%.1f\t%.1f\t%.1f\n", b, trunc(b), floor(b), ceil(b), round(b));
printf("%.1f\t%.1f\t%.1f\t%.1f\t%.1f\n", c, trunc(c), floor(c), ceil(c), round(c));
printf("%.1f\t%.1f\t%.1f\t%.1f\t%.1f\n", d, trunc(d), floor(d), ceil(d), round(d));
printf("%.1f\t%.1f\t%.1f\t%.1f\t%.1f\n", e, trunc(e), floor(e), ceil(e), round(e));
return 0;
}
运行截图:
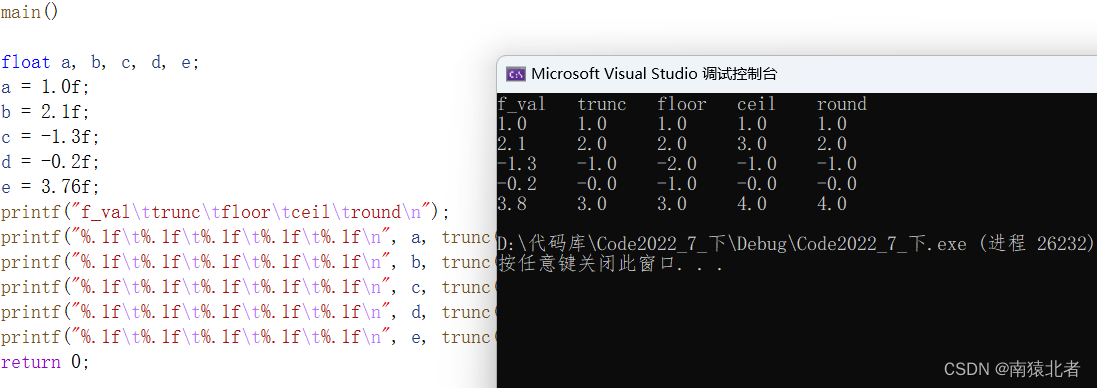
头文件:#include<math.h>
trunc()函数是向0取整;
floor()函数是向负无穷取整;
ceil()函数是向正无穷取整;
round()函数是四舍五入取整;
C语言中采用的是向0取整;
例如在C语言中
-3.14取整是-3;
在python中采用的是向负无穷取整;
在python中-3.14取整是-4;
2、 聊聊取模
取模概念:如果a和d是自然数,d非0,可以证明存在两个唯一的整数q和r,满足a=q*d+r,且0<=r<d,其中q被称为商,r被称为余数;
那么接下来我们来看看以下代码;

其中10=(q)*3+(r)
按照向0取整的原则,q=3,故r=1;
那如果是负数呢?

按照上述规矩:
-10=(q)3+(r);
向0取整原则:q=-3,故r=-1;

这似乎于上文的定义有一些冲突,r<0了,为了解决这一问题,我们重新修订了定义:如果a和d是自然数,d非0,可以证明存在两个唯一的整数q和r,满足a=qd+r,且0<=|r|<|d|,其中q被称为商,r被称为余数;
有了这样的定义,C语言中r为负数也就能解释的通了;
上文不是说,在python中的取整方式不一样吗?那么-10/3与-10%3的结果一样吗?

通过验证发现结果是不一样的:
分析:-10/3是-3.33333…,按照负无穷的取整方式,-10/3就应该是-4;
同理:-10=(q)*3+(r);q=-4,故r=2;
3、是什么决定了这种现象?
通过上文分析,我们得出
在C语言中,-10%3=-1;
在python中,-10%3=2;
那么是由于什么原因呢?我们知道,余数是由商确定的,那商又是由什么确定的?是由于取整方式啊;在C语言和python中二者取整方式的差异,造成了“取模”的差异;也就也为这%运算符,在不同的语言中,意义是不一样的;
4、取模和取余一样吗?
大多数时候他们是一个意思,但严谨来说并不是这样的:
取模:取商的方式是按照像负无穷取整的方式;
取余:取商的方式是按照像0取整的方式;
对于C语言来说%代表着取余;
对于python来说%代表取模;
那么如何判断一种语言%代表的是取余还是取模呢?
你可以用以下代码去测试:
C语言(或C++)语言下,%是取余运算;
int main()
{
int a = -10;
int b = 3;
if (a / b == -3)
{
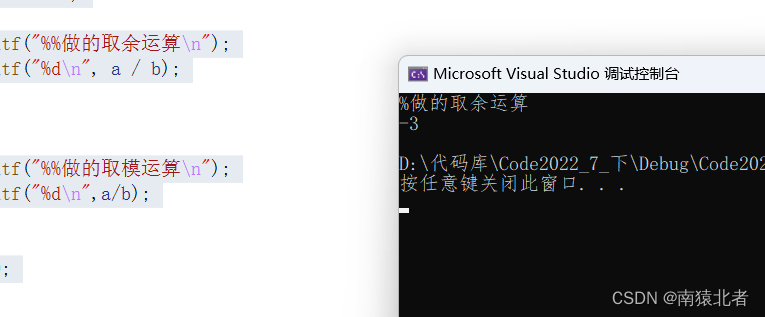
printf("%%做的取余运算\n");
printf("%d\n", a / b);
}
else
{
printf("%%做的取模运算\n");
printf("%d\n",a/b);
}
return 0;
}