序
最近一直在致力于LQR的c语言工程实现,从LQR工程实现的调研到使用QR求矩阵逆,再到今天的LQR的C语言的实现,从底层一步一步去写算法,这种感觉让我回忆起在哈工大读硕期间,和算法能力非常强的泽哥合作时,他将复杂的空间三维立体路径规划问题,一步一步拆分成可用计算机语言去处理的逻辑,我在他的引导下顺利完成了代码的编写,对他的算法能力甚是佩服。转眼间已经毕业满一年了,我们保持着联系,我们时常在讨论,作为工程师的我们究竟在个人的职业生涯中要做成什么样的?我们究竟想要成为一个什么样的工程师?是每天在重复做调参?还是在重复写业务逻辑的工程师?还是…
每当我想做一个东西或者想学习一个技术时,我特别喜欢去谷歌搜索一下,用英文去搜索相关的文章,我发现国外有些工程师写的文章就是真的好,以工程实现为导向,实时求实,从基础的数学原理开始写起,我记得查QR分解时,有个国外的工程师,从零用C++开始写QR分解,然后用它去上课教学生,我就觉得挺不错,很有意义。
于个人来说,这些东西,可以加深你对算法的理解,QR分解的目的是?要想矩阵逆,首先要QR分解,然后再求上三角矩阵的逆,这些具体的算法如果不懂没关系,但是要能看懂所给的数学结论,然后用这些数学结论的公式去编写代码。或许,从底层算法开始写起,是一个核心工程师需要有的过程。
所以,到底成为一个什么样的工程师呢?
因为CSDN提示文字较少,于是就写了随笔,希望以后能有更多的时间和精力去学习和写文章。
终于凑够字数了。。。。。开始正文。
本文主要写明了LQR的C语言工程实现,具体实现步骤参见我之前写的技术博客LQR工程实现(调研),c代码在我的github仓库https://github.com/JackJu-HIT/SolutionToRiccatiForLQR。
笔者对c工程代码的控制率K求解和MATLAB自带的K=dlqr(A,B,Q,R),做了一个矩阵对比,感觉效果还行,如果有问题,也欢迎私信讨论。
1.MATLAB代码实现
首先使用MATLAB实现LQR求解如下
%Function:离散黎卡提方程求解
%Author:Jack Ju
%Date:2022-7-3 13:05
clear
%被控对象状态方程
A=[0 1 0
0 0 0
-7 -41 6];
B = [0
0
1];
C = [6 0 0];
Q = [1 0 1
0 1 0
0 0 1];
R=2;
%[1 0 0
% 0 1 0
% 0 0 0];
tolerance = 0.1;%迭代收敛条件
times =50; %迭代次数
[res_P ] = Riccati(Q,R,A,B,C,tolerance,times)%求解黎卡提方程
K=(R+B'*res_P*B)^(-1) *B'*res_P*A
%A'*res_P*A-A'*res_P*B*(R+B'*res_P*B)^(-1)*B'*res_P*A+Q-res_P %结果验证
%%A'*POBS*A
function [res_p P_next_ POBS] = Riccati(Q,R,A,B,C,tolerance,times)
P=[];
P=Q;
%%res = [];
P_next_ = [];
resP=[0];
POBS = [];
for i = 1:1:times
P_next = A'*P*A-A'*P*B*(R+B'*P*B)^(-1)*B'*P*A+Q;
P_next_ = [P_next_ P_next];
if abs(norm(P_next)-norm(P))<tolerance
res_p = P_next; %存储结果
%% flag =true;
%%return res;
break;
end
P=P_next;
end
end
2.使用C语言工程实现如下
目前的C语言版本已经是可以正常运行的版本,要求输入矩阵控制B矩阵必须是1列的。
完整工程参见我的github仓库https://github.com/JackJu-HIT/SolutionToRiccatiForLQR
/**
* @Function:Solution for Riccati
* @Date:2022-07-18 14:00:00
* @Author:juchunyu
* @Last modified:juchunyu
*/
#include <stdio.h>
#include <math.h>
#define SIZE 3
#define SIZE_ 1
int main(){
double A[SIZE][SIZE] = {0,1,0,0,0,1,-7,-41,6};
double B[SIZE] = {0,0,1};
double C[SIZE] = {6,0,0};
double Q_C[SIZE][SIZE] = {1,0,1,0,1,0,0,0,1};
double R_C[SIZE_ ][SIZE_ ] = {2};
double AT[SIZE][SIZE] = {0};
double BT[SIZE] = {0};
double P_Result[SIZE][SIZE] = {0};
double P[SIZE][SIZE] = {1,0,1,0,1,0,0,0,1}; //P的初始值设定为Q矩阵
int times = 50; //迭代最大次数限制
double tolerance = 0.01; //迭代精度设置
int IsResult = 0;
double K[SIZE] = {0};
int CalTimes = 0; //实际迭代次数
//计算A的转置
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
AT[j][i] = A[i][j];
}
}
//计算B的转置
for(int i = 0;i < SIZE;i++){
BT[i] = B[i];
}
/*P_next = A'.*P.*A-A'.*P.*B.*(R+B'.*P.*B)^(-1).*B'.*P.*A+Q*/
for(int t = 0;t < times;t++){
double P_next[SIZE][SIZE] = {0};
double ATP[SIZE][SIZE] = {0};
double ATPA[SIZE][SIZE] = {0};
double ATPB[SIZE] = {0};
double BTP[SIZE] = {0};
double BTPA[SIZE] = {0};
double BTPB = 0;
double RBTPB[SIZE_][SIZE_] = {0};
double RBTPBINVERSE[SIZE_][SIZE_] = {0};
double ATPBRBTPBINVERSE[SIZE] = {0};
double ATPBRBTPBINVERSEBTPA[SIZE][SIZE] = {0};
//计算A'*P
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
for(int k = 0;k < SIZE;k++){
ATP[i][j] += AT[i][k] * P[k][j];
}
}
}
//计算A'*P*A
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
for(int k = 0;k < SIZE;k++){
ATPA[i][j] += ATP[i][k] * A[k][j];
}
}
}
//计算A'*P*B
for(int i = 0;i < SIZE;i++){
for(int k = 0;k < SIZE;k++){
ATPB[i] += ATP[i][k] * B[k];
}
}
//计算B'*P
for(int i = 0;i < SIZE;i++){
for(int k = 0;k < SIZE;k++){
BTP[i] += B[k] * P[k][i];
}
}
//计算B'*P*A
for(int i = 0;i < SIZE;i++){
for(int k = 0;k < SIZE;k++){
BTPA[i] += BTP[k] * A[k][i];
}
}
//计算B'*P*B
for(int i = 0; i < SIZE; i++){
BTPB += BTP[i] * B[i];
}
//计算R+B'*P*B
for(int i = 0;i < SIZE_;i++){
for(int j = 0;j < SIZE_;j++){
RBTPB[i][j] += R_C[i][j] + BTPB;
}
}
/******************************************开始计算(R+B'*P*B)^(-1)********************************************************/
double Q[SIZE_][SIZE_] = {0};
double R[SIZE_][SIZE_] = {0};
double v[SIZE_] = {0};
double QT[SIZE_][SIZE_] = {0};
double RInverse[SIZE_][SIZE_] = {0};
double m_in[SIZE_][SIZE_] = {0};
double m_inverse_[SIZE_][SIZE_] = {0};
double m_inverse[SIZE_][SIZE_] = {0};
int length = SIZE_;
/**进行QR分解**/
for(int k = 0;k < length;k++){
/*R(1:k-1,k) = Q(:,1:k-1)’ * A(:,k)*/
if(k >= 1){
for(int i = 0;i < k;i++){
for(int j = 0;j < length;j++){
R[i][k] += Q[j][i]*RBTPB[j][k];
}
}
}
/*v = A(:,k) - Q(:,1:k-1) * R(1:k-1,k)*/
for(int j = 0;j<length;j++){
if(k < 1){
v[j] = RBTPB[j][0];
} else {
v[j] = RBTPB[j][k];
for(int g = 0;g < k;g++){
v[j] -= R[g][k]*Q[j][g];
}
}
}
/*R(k,k) = norm(v)*/
for(int i = 0;i < length;i++){
R[k][k] += v[i]*v[i];
}
R[k][k] = sqrt(R[k][k]);
/*Q(:,k) = v / R(k,k)*/
for(int i = 0;i < length;i++){
Q[i][k] = v[i]/R[k][k];
}
}
//求解Q的转置
for(int i = 0;i < length;i++){
for(int j = 0;j<length;j++){
QT[j][i] = Q[i][j];
}
}
/**求解R的逆矩阵***/
//转置
for(int i = 0;i < length;i++){
for(int j = 0;j < length;j++){
m_in[j][i] = R[i][j];
}
}
for(int j = 0;j < length;j++){
//求解对角线
m_inverse_[j][j] = 1/m_in[j][j];
for(int i = j+1;i < length;i++){
double temp = 0;
for(int k = j;k <= i-1;k++){
temp += m_in[i][k]*m_inverse_[k][j];
}
m_inverse_[i][j] = -temp/m_in[i][i];
}
}
//tranpose
for(int i = 0;i < length;i++){
for(int j = 0;j < length;j++){
m_inverse[j][i] = m_inverse_[i][j]; //逆矩阵
}
}
/*A = QR => A^(-1) = R^(-1)*Q^T*/
for(int i = 0;i < length;i++){
for(int j = 0;j < length;j++){
for(int k = 0;k < length;k++){
RBTPBINVERSE[i][j] += m_inverse[i][k]*QT[k][j];
}
}
}
/****************************************************************结束(R+B'*P*B)^(-1)求解********************************************/
//计算A'*P*B*(R+B'*P*B)^(-1)
for(int i = 0;i < SIZE;i++){
for(int k = 0;k < SIZE_;k++){
ATPBRBTPBINVERSE[i] += ATPB[i] * RBTPBINVERSE[k][0];
}
}
//计算A'*P*B*(R+B'*P*B)^(-1)*B'*P*A
for(int i = 0;i < SIZE;i++){
for (int j = 0; j < SIZE; j++){
ATPBRBTPBINVERSEBTPA[i][j] = ATPBRBTPBINVERSE[i] * BTPA[j];
}
}
/*P_next = A'.*P.*A-A'.*P.*B.*(R+B'.*P.*B)^(-1).*B'.*P.*A+Q*/
for(int i = 0;i< SIZE;i++){
for (int j = 0; j < SIZE; j++){
P_next[i][j] = ATPA[i][j] - ATPBRBTPBINVERSEBTPA[i][j] + Q_C[i][j];
}
}
//判断是否收敛
double P_maxCoeff = 0;
double P_max[SIZE][SIZE] = {0};
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
P_max[i][j] = (P[i][j] - P_next[i][j]) > 0 ? (P[i][j] - P_next[i][j]):-(P[i][j] - P_next[i][j]) ;
}
}
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
if(P_max[i][j]>P_maxCoeff)
P_maxCoeff = P_max[i][j];
}
}
/*
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
if(P[i][j]>P_maxCoeff)
P_maxCoeff = P[i][j];
}
}
*/
/*
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
P_maxCoeff += P[i][j] * P[i][j];
}
}
P_maxCoeff = sqrt(P_maxCoeff);
*/
double P_next_maxCoeff = 0;
/*
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
if(P_next[i][j]>P_maxCoeff)
P_next_maxCoeff = P[i][j];
}
}
*/
/*
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
P_next_maxCoeff = P_next[i][j] * P_next[i][j];
}
}
P_next_maxCoeff = sqrt(P_next_maxCoeff);
*/
/*
if((P_next_maxCoeff - P_maxCoeff) > 0){
if((P_next_maxCoeff - P_maxCoeff) < tolerance){
//将P_Next赋值给P_Result
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
P_Result[i][j] = P_next[i][j];
}
}
IsResult = 1;
break;
}
}
if((P_next_maxCoeff - P_maxCoeff) < 0){
if(-(P_next_maxCoeff - P_maxCoeff) < tolerance){
//将P_Next赋值给P_Result
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
P_Result[i][j] = P_next[i][j];
}
}
IsResult = 1;
break;
}
}
*/
if(P_maxCoeff < tolerance){
//将P_Next赋值给P_Result
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
P_Result[i][j] = P_next[i][j];
}
}
IsResult = 1;
break;
}
//将P_Next赋值给P_Result
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
P_Result[i][j] = P_next[i][j];
}
}
//将P_Next赋值给P
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;j++){
P[i][j] = P_next[i][j];
}
}
/***K = (R+B'PB)^(-1)*B'P*A **/
for(int i = 0;i < SIZE;i++){
K[i] = RBTPBINVERSE[0][0] * BTPA[i];
}
CalTimes++;
}
if(IsResult == 1){
printf("矩阵P_Result的结果:\n");
for(int i = 0;i < SIZE;i++){
for(int j = 0;j < SIZE;++j){
printf("%2.4f ", P_Result[i][j]);
}
printf("\n");
}
printf("控制率矩阵K的结果:\n");
for(int i = 0;i < SIZE;i++){
printf("%2.4f ", K[i]);
printf("\n");
}
printf("离散立卡提方程迭代次数为:%d",CalTimes);
printf("\n");
} else {
printf("对不起矩阵P_Result的结果为空!");
}
}
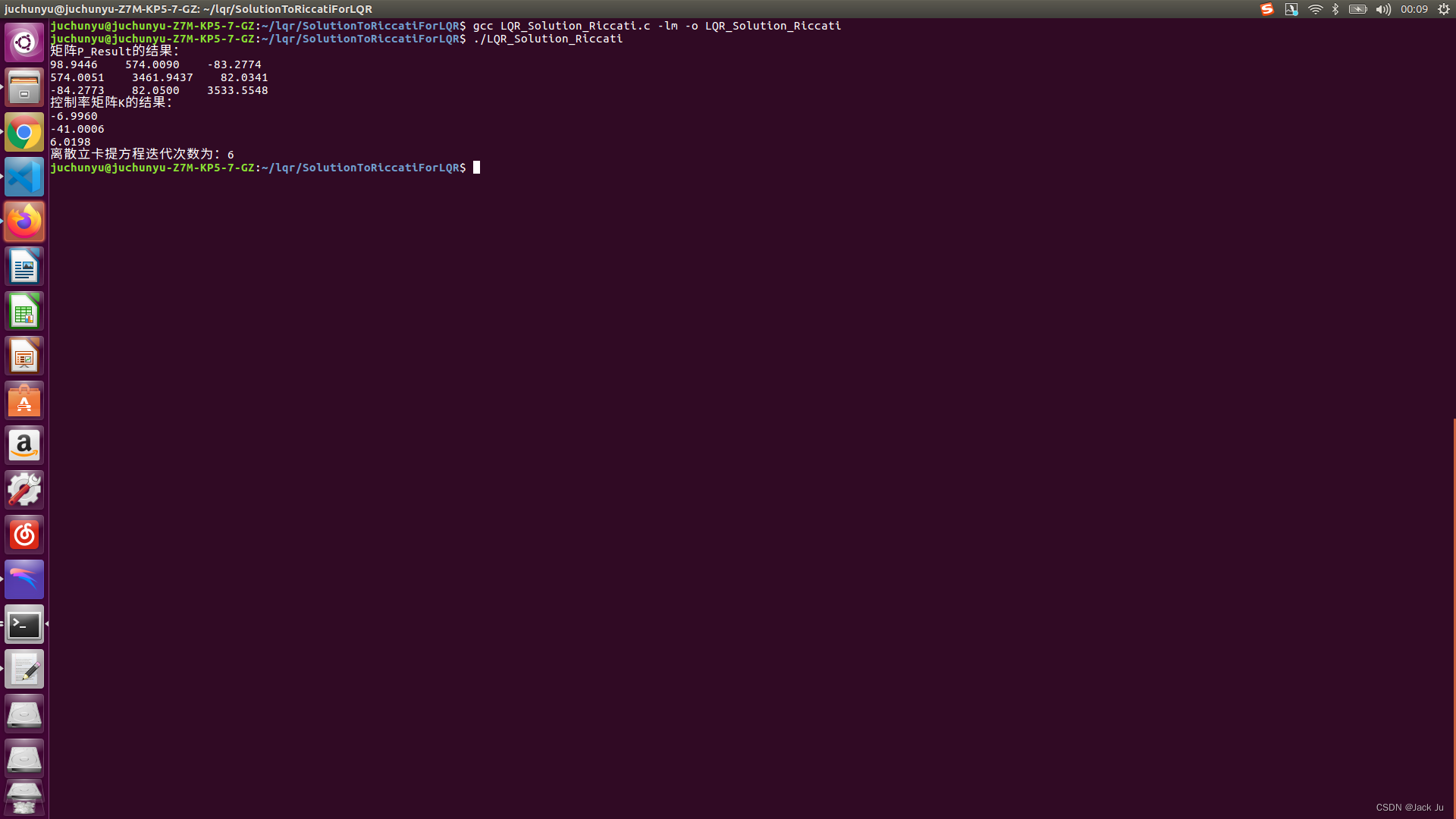
Linux下运行效果如下图: