104.二叉树的最大深度
题目描述[简单]:
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
示例1:
输入: [3,9,20,null,null,15,7]
输出:3
思路[递归]:
本题跟昨天的题思路都是一样的,都可以用递归来做。
首先要列出为空的情况,此时输出0;
当有结点之后,我们要比较左子树的深度值和右子树的深度值,看哪个最大。这里有个点需要注意:我们要算上最上头的那个根节点root。所以return的时候要+1 。
看左子树和右子树的深度,就是看左子树的子树深度,这就是递归的思想。
终止递归条件:树遍历到底部,子树为空。
C++代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == NULL)
return 0;
return max(maxDepth(root->left),maxDepth(root->right)) + 1;
}
};
108.将有序数组转换为二叉搜索树
题目描述[简单]:
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例1:
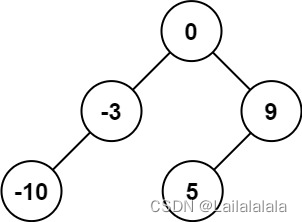
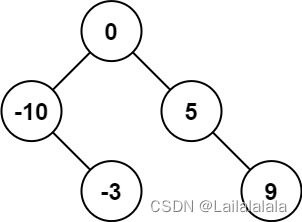
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]/[0,-10,5,null,-3,null,9]
 ————————
———————— 
思路[递归]:
本题依旧是递归的思想。
本题的题目是给出了一个有序数组,然后再来创建BST。众所周知,BST的中序遍历就是数组的升序排列,因此本题可以变成:
通过BST的中序序列来推断这棵BST树的层序遍历序列。
我们可以在升序序列中的任取一个元素作为根节点,将该元素左边元素进行升序排列从而构建左子树,将该元素右边元素进行升序排列从而构建右子树。又因为是高度平衡的树,所以我们选择升序序列的中间元素作为根节点。
C++代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return sortedArray(nums , 0 , nums.size()-1);
}
TreeNode* sortedArray(vector<int>& nums , int l , int r){
if(r<l)//如果数组为空
return nullptr;//直接返回空结点
int mid = l + (r-l) / 2;// 以升序数组的中间元素作为根节点 root
TreeNode* root = new TreeNode(nums[mid]);//把中间节点作为根节点
root->left = sortedArray(nums, l, mid - 1);// 通过递归的方式来构建 root 的左子树
root->right = sortedArray(nums, mid + 1, r);//通过递归的方式来构建 root 的右子树
return root;
}
};
109.将有序链表转换为二叉搜索树
题目描述[中等]:
给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为高度平衡的二叉搜索树。
其中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。
示例 1:
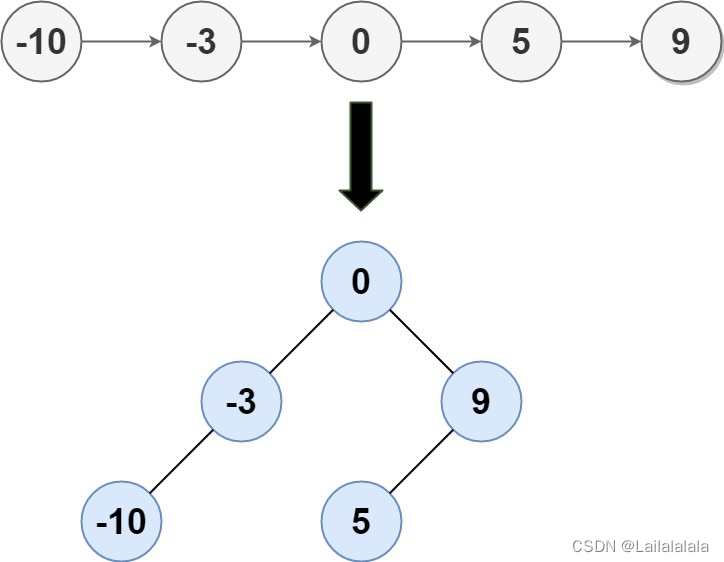
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0,-3,9,-10,null,5],它表示所示的高度平衡的二叉搜索树。
思路[递归+双指针]:
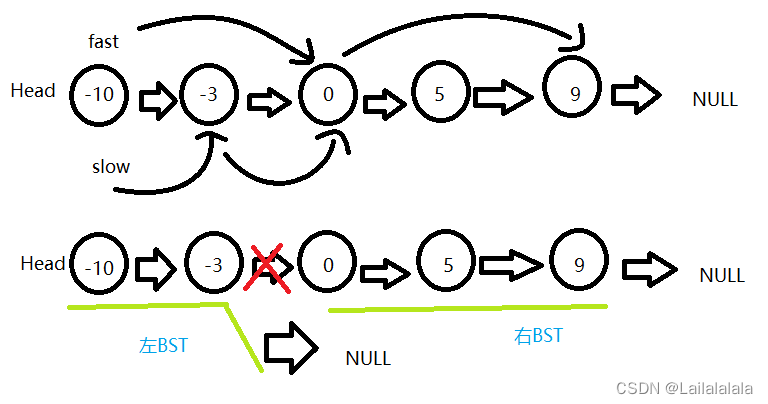
这种题第一次看见就觉得不知道如何下手,感觉可以用递归写,但是不知道怎么找中间结点,就是怎么把他们联系起来,然后我看题解说可以用双指针——快慢指针。快指针一次走两步,慢指针一次走一步。
那么链表的中间结点方法:
快慢指针最初都指向头结点,分别一次走两步和一步,当快指针走到尾节点时,慢指针正好走到链表的中间。此时断成两个链表,将其分开。
实现链表断开的方法:
建立一个空指针用来保存慢指针的前一个节点,从而实现断开操作。而保存前一个而不是当前那个的原因是:单向链表的结点没有前驱指针。
C++代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
if(head==nullptr)
return nullptr;
if(head->next == nullptr) //如果只有一个节点
return new TreeNode(head->val); //直接创建,然后返回
ListNode* mid = getMid(head);//调用中间值方法
//构造二叉树
TreeNode* root = new TreeNode(mid->val);//此时根节点就是中间节点
root->left = sortedListToBST(head);//递归构造左子树,由于链表在中间节点前断开,所以直接传入头结点
root->right = sortedListToBST(mid->next);//递归构造右子树,此时传入中间节点的下一个节点
return root;
}
ListNode* getMid(ListNode* head){//获取链表中间节点的方法,在获得中间值同时还要把链表在中间值前断开(方便递归操作)
ListNode* node = nullptr;//定义一个空指针
ListNode* fast = head;//利用双指针来找中间节点,此时定义两个指针,快指针和慢指针
ListNode* slow = head;
while(fast && fast->next){
fast = fast->next->next;//快指针一次移动两步
node = slow;//更新node指针
slow = slow->next;//慢指针一次移动一步
}
if(node!=nullptr)//移动结束后,node非空,就在此断开链表
node->next = nullptr;
return slow;
}
};
时间复杂度:O(nlogn);