[C++知识库]【C++/STL】手撕AVL树

1.map中的问题

1. map是关联容器，它按照特定的次序(按照key来比较)存储由键值key和值value组合而成的元
   素。

2. 在map中，键值key通常用于排序和惟一地标识元素，而值value中存储与此键值key关联的内容。键值key和值value的类型可能不同，并且在map的内部，key与value通过成员类型value_type绑定在一起，为其取别名称为pair:

   typedef pair<const Key,T> value_type
   

3.在内部，map中的元素总是按照键值key进行比较排序的。

4.map中通过键值访问单个元素的速度通常比unordered_map容器慢，但map允许根据顺序对元素进行直接迭代(即对map中的元素进行迭代时，可以得到一个有序的序列)。

5.map支持下标访问符，即在[]中放入key，就可以找到与key对应的value。

6.map通常被实现为二叉搜索树(更准确的说：平衡二叉搜索树(红黑树))

1.1map的insert()函数剖析

函数原型

返回值

insert()如果成功，那么返回值pair<iterator,bool>中的bool为true,表示插入成功；迭代器iterator指向插入的位置。

insert()如果插入失败，那么返回值pair<iterator,bool>中的bool值为false,表示插入失败，说明map中已经有val->key关键字相同的数据，迭代器iterator指向map中与关键字val->key相等的位置。

比如

map<string, int>mp;
mp.insert(make_pair("桃子", 2));
mp.insert(make_pair("梨", 3));
auto it=mp.insert(make_pair("苹果", 4));
//此时it指向的是苹果的结点

当我们再插入一个梨的数据时

pair<map<string, int>::iterator, bool> it = mp.insert(make_pair("桃子", 6));

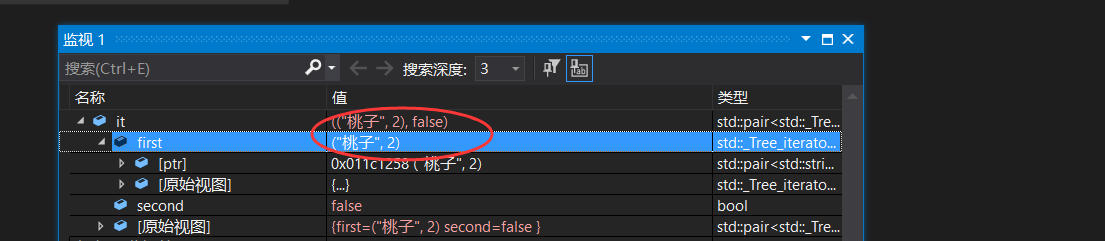
此时迭代器指向的是(“桃子”,2)的位置

1.2map对[ ]的重载

函数原型

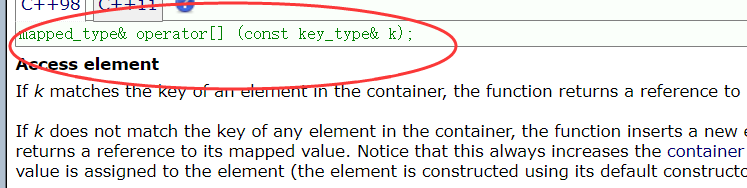
实现方式

(*((this->insert(make_pair(k,mapped_type()))).first)).second;
//上面的表达式过于的臃肿，我们进行简化
auto it=this->insert(make_pair(k,mapped_type());
                //这一步会创建一个键值对<K,V>
                     
//上面的表达式可以表示为
((*it).first)->second;
//相当于使用insert返回值pair<iterator,bool>中，迭代器中的value值

所以我们在向map中添加数据时，有下面的写法：

void test_map2()
{
	string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
	map<string, int> countMap;
	for (auto& str : arr)
	{
		countMap[str]++;
	}
}
/*
会出现两种情况：
情况一：
	当coutMap中没有对应关键字的数据，那么会先创建一个键值对<K,V>，在通过=赋值给对应的变量的value。
	
	
情况二：
	当coutMap中有对应的关键字是,那么会指向有相同关键字的键值对<K-V>的value
*/

2.AVL树的模拟实现

2.1AVL树的概念

? 二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。

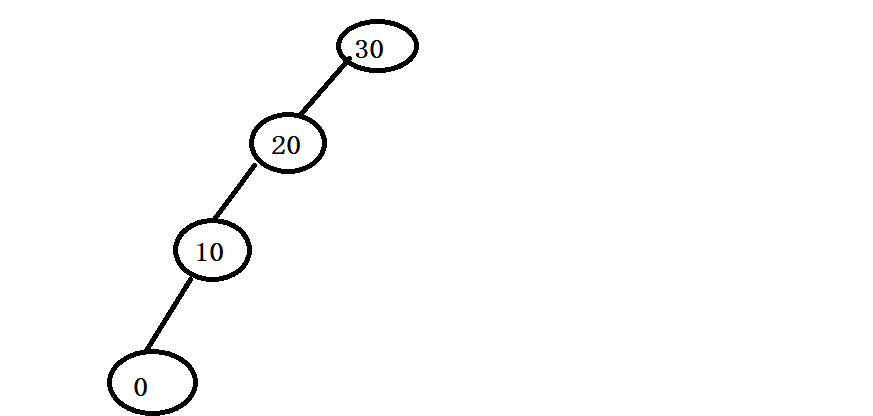
为了解决二叉搜索树的退化问题：

? 两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：**当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。 **

一棵AVL树有下面的性质

• 它的左右子树都是AVL树
• 左右子树的高度差的绝对值不超过2(高度差为-1 1 0 )

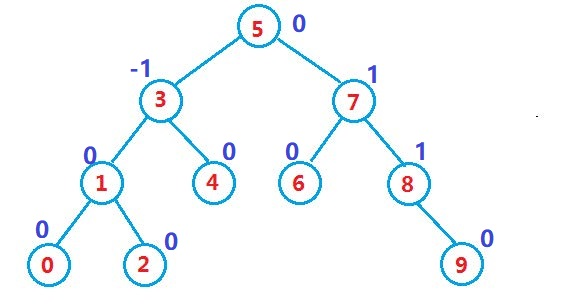
我们规定平衡因子bf为：右子树的高度-左子树的高度

template <class K,class V>
class AVLTree
{
public:
	typedef AVLTreeNode<K, V> Node;

	//构造函数
	AVLTree()
		:_root(nullptr)
	{}
    /*
    	内部函数实现
    	....................
    	....................
    	....................
    	....................
    */
private:
    Node* _root;
}

2.2AVL树节点的定义

template <class K,class V>
struct  AVLTreeNode
{
	AVLTreeNode<K,V>* _left;  //左子树
	AVLTreeNode<K,V>* _right; //右子树
	AVLTreeNode<K,V>* _parent; //父亲节点
	pair<K, V>_kv;	//存放的K-V键值对
	//左右子树的高度差
	int _bf; //平衡因子
	//构造函数
	AVLTreeNode(const pair<K,V>& kv)
		:_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0),_kv(kv)
	{}
};

2.3AVL树的插入

? AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步：

• 按照二叉搜索树的方式插入新节点
• 调整节点的平衡因子

插入新节点

1.第一步插入数据和一般的二叉搜索树一样

2.更新平衡因子

cur插入后，parent的平衡因子一定需要调整，在插入之前，parent
的平衡因子分为三种情况：-1，0, 1, 分以下两种情况：

1. 如果cur插入到parent的左侧，只需给parent的平衡因子-1即可
2. 如果cur插入到parent的右侧，只需给parent的平衡因子+1即可
   此时：pParent的平衡因子可能有三种情况：0，正负1， 正负2
   1. )如果parent的平衡因子为0，说明插入之前pParent的平衡因子为正负1，插入后被调整成0，此时满足AVL树的性质，插入成功。不需要再继续向上调整。
   2. ) 如果parent的平衡因子为正负1，说明插入前parent的平衡因子一定为0，插入后被更新成正负1，此时以parent为根的树的高度增加，需要继续向上更新
   3. ) 如果parent的平衡因子为正负2，则parent的平衡因子违反AVL树的性质，需要对其进行旋转处理

bool insert(const pair<K, V>& kv)
	{
		//按照普通的搜索二叉树的规则插入
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_bf = 0;
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		//比较K
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		cur->_parent = parent;
		if (kv.first > parent->_kv.first)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		//更新_bf平衡因子
		while (parent)
		{
			if (parent->_left == cur)
			{
				parent->_bf--;
			}
			else if (parent->_right == cur)
			{
				parent->_bf++;
			}

			if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == -2 || parent->_bf == 2)
            {
    		 /*
     			旋转：
     			一共右四种情况，分别会对应
     			左单旋			右单旋
             	左右单旋		右左单旋
     .......................................
     .......................................
     .......................................
     		*/
            }
}

1.）在较高的右子树右侧插入数据(左单旋)

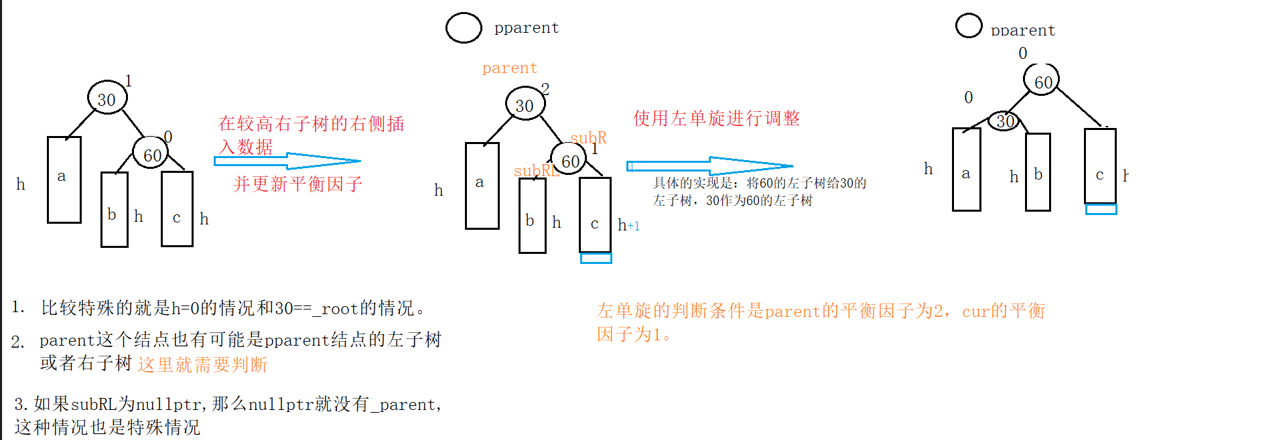
if (parent->_bf == 2 && cur->_bf == 1)
{
	//左单旋
	RouteL(parent);
}

//左单旋的实现
void RouteL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	Node* pparent = parent->_parent;
	parent->_right = subRL;
	if (subRL)
	{
		subRL->_parent = parent;
	}
	subR->_left = parent;
	parent->_parent = subR;
	//如果root为根
	if (parent == _root)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		subR->_parent = pparent;
		if (parent == pparent->_left)
		{
			pparent->_left = subR;
		}
		else
		{
			pparent->_right = subR;
		}
	}
	//更新平衡因子
	parent->_bf = 0;
	subR->_bf = 0;
}

2.)在较高的左子树左侧插入数据(右单旋)

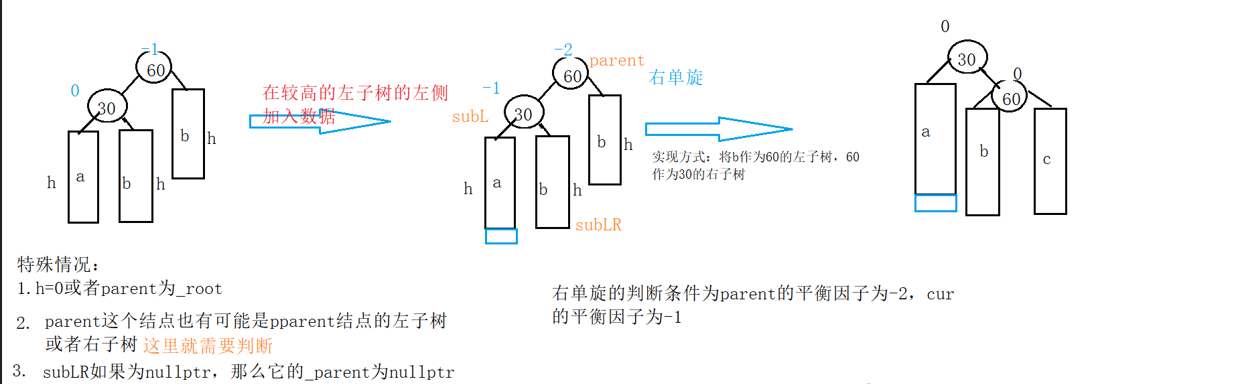
else if (parent->_bf == -2 && cur->_bf == -1){
	RouteR(parent);
}

//右单旋
void RouteR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	parent->_left = subLR;
	if (subLR)
	{
		subLR->_parent = parent;
	}
	subL->_right = parent;
	Node* pparent = parent->_parent;
	parent->_parent = subL;
	if (parent == _root)
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else
	{
		if (pparent->_left == parent)
		{
			pparent->_left = subL;
		}
		else
		{
			pparent->_right = subL;
		}
		subL->_parent = pparent;
	}
	//平衡因子调整
	parent->_bf = 0;
	subL->_bf = 0;
}

3.)在较高的左子树的右侧插入数据(左右双旋)

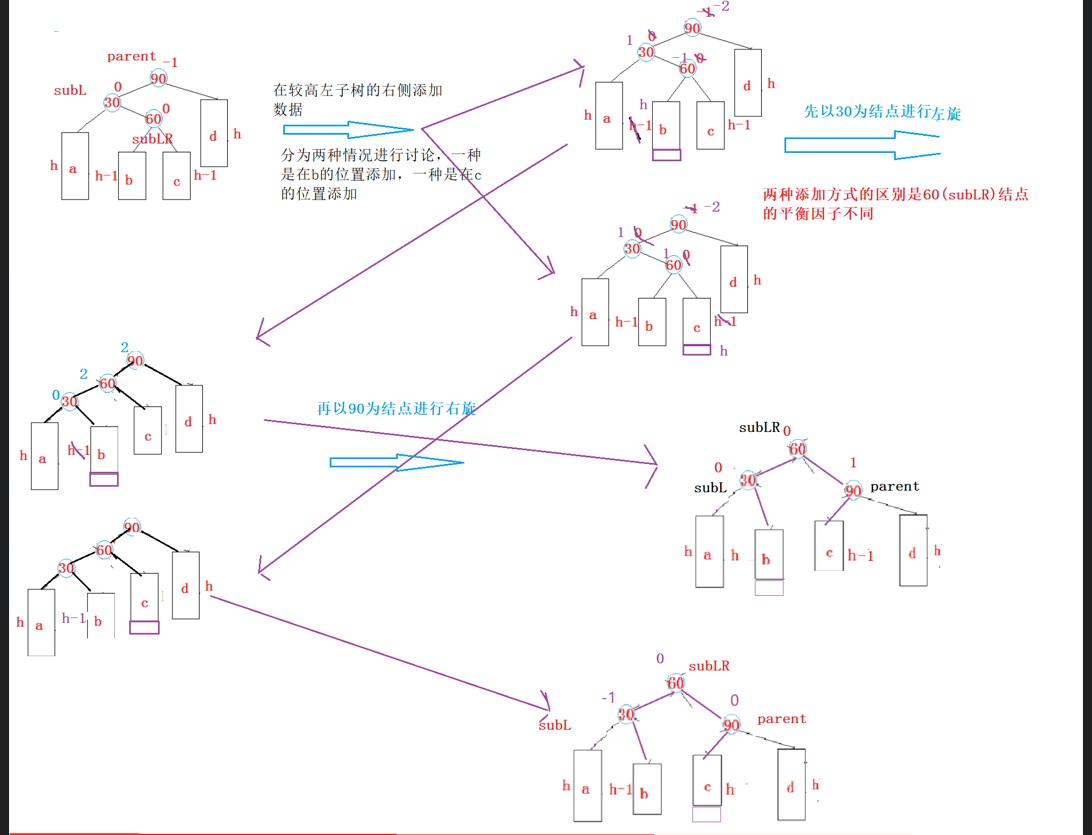
还有一种h==0的特殊情况

else if (parent->_bf == -2 && cur->_bf == 1)
{
	RouteLR(parent);
}

void RouteLR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	int bf = subLR->_bf;
	RouteL(subL);
	RouteR(parent);
	if (bf == -1)
	{
		subLR->_bf = 0;
		subL->_bf = 0;
		parent->_bf = 1;
	}
	else if (bf == 1)
	{
		subLR->_bf = 0;
		subL->_bf = -1;
		parent->_bf = 0;
	}
	else if (bf == 0)
	{
		subLR->_bf = 0;
		subL->_bf = 0;
		parent->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

4.)在较高的右子树的左侧插入数据(右左双旋)

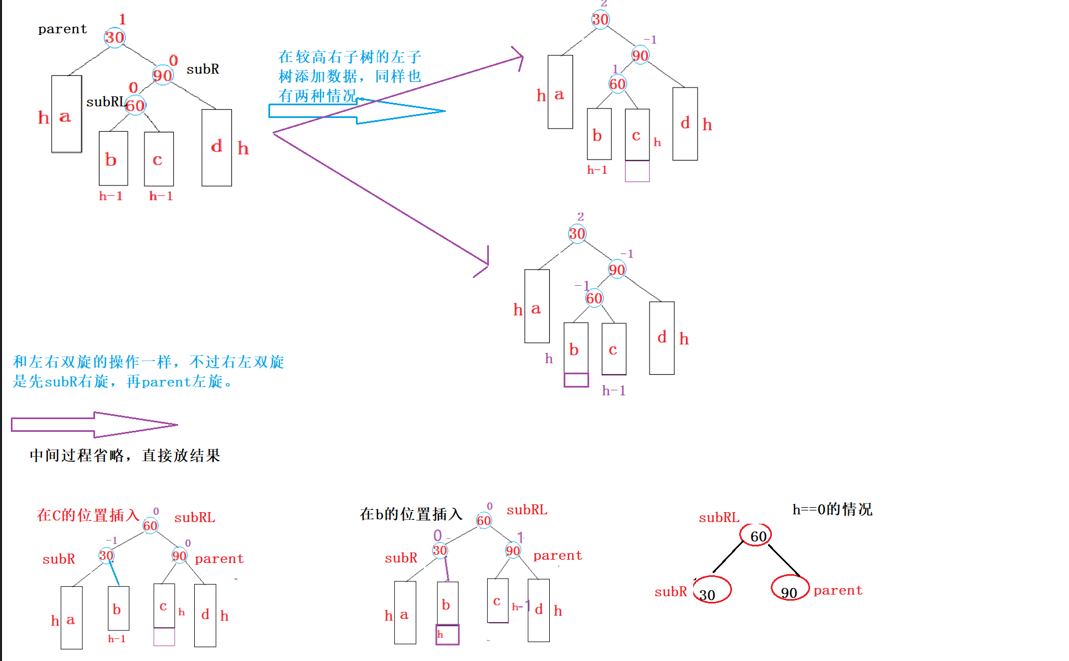
else if (parent->_bf == 2 && cur->_bf == -1)
{
	RouteRL(parent);
}

void RouteRL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	int bf = subRL->_bf;
	RouteR(subR);
	RouteL(parent);
	if (bf == 0)
	{
		subR->_bf = 0;
		subRL->_bf = 0;
		parent->_bf = 0;
	}
	else if (bf == -1)
	{
		subRL->_bf = 0;
		parent->_bf = 0;
		subR->_bf = 1;
	}
	else if (bf == 1)
	{
		subRL->_bf = 0;
		parent->_bf = -1;
		subR->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

2.4验证是否为AVL树

我们只需要验证每棵子树平衡因子的绝对值是否小于2，平衡因子与高度差是否相等即可。

int _Height(Node* root)
{
	if (root == nullptr)
	{
		return 0;
	}
	int left = _Height(root->_left);
	int right = _Height(root->_right);
	return max(left, right) + 1;
}

//判断是否为平衡二叉树
bool _isAVLTree(Node* root)
{
	if (root == nullptr)
	{
		return true;
	}
	int height_left = _Height(root->_left);
	int height_right = _Height(root->_right);
	int bf = height_right - height_left;
	if (abs(bf) >= 2)
	{
		cout << "平衡因子异常，不是平衡二叉树" << endl;
		return false;
	}
	if (bf != root->_bf)
	{
		cout << "平衡因子计算错误" << endl;
		return false;
	}
	return _isAVLTree(root->_left) && _isAVLTree(root->_right);
}

bool isAVLTree()
{
	return _isAVLTree(_root);
}

2.5层序遍历

和一般的多叉树层序遍历一样，借助一个queue<Node*>

void _levelOrderBottom(Node* root) {
	if (root == nullptr)
	{
		return;
	}
	queue<Node*>q;
	q.push(root);
	while (!q.empty())
	{
		int size = q.size();
		for (int i = 0;i < size;i++)
		{
			Node* front = q.front();
			cout << front->_kv.second << " ";
			if (front->_left)
			{
				q.push(front->_left);
			}
			if (front->_right)
			{
				q.push(front->_right);
			}
			q.pop();
		}
		cout << endl;
	}
}
//层序遍历
void levelOrderBottom()
{
	_levelOrderBottom(_root);
}

2.6中序遍历

//中序遍历
void _inorder(Node* root)
{
	if (root == nullptr)
	{
		return;
	}
	_inorder(root->_left);
	cout << root->_kv.first << " ";
	_inorder(root->_right);
}

void inorder()
{
	_inorder(_root);
}

3.实现结果

我们可以向AVLTree中添加随机数，再调用isAVLTree()和中序遍历验证。如果isAVLTree()返回1，并且中序遍历的结果是升序，那么就是一棵AVLTree。

int main()
{
	srand(time(0));
	AVLTree<int, int>avl;
	int N = 100;
	for (int i = 0;i < N;i++)
	{
		int m = rand();
		avl.insert(make_pair(m, m));
	}
	cout << avl.isAVLTree() << endl;
	avl.inorder();
	//avl.levelOrderBottom();
}

感谢阅读！