开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> C++知识库 -> [C++](19)AVL树插入，旋转，详细图解与代码 -> 正文阅读

[C++知识库][C++](19)AVL树插入，旋转，详细图解与代码

概念

在计算机科学中，AVL树（以发明者 Adelson-Velsky 和 Landis 命名）是一种自平衡的二叉搜索树（BST）。

特点：

本身首先是一棵二叉搜索树。
带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

也就是说，AVL树，本质上是带了平衡功能的二叉搜索树。

框架

我们把它设计成三叉链表，即每个结点不仅可以找到它的左右孩子结点，也可以找到它的父亲结点。为了方便平衡，每个结点给一个平衡因子（balance factor）

template<class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	// 右子树-左子树高度差
	int _bf;	// balance factor

	AVLTreeNode(const pair<K, V>& kv)
		: _kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};

template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:

private:
	Node* _root;
};

插入

按搜索树规则插入

bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        _root->_bf = 0;
        return true;
    }

    Node* parent = nullptr;
    Node* cur = _root;
    while (cur)
    {
        if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }
    cur = new Node(kv);
    if (parent->_kv.first < kv.first)
        parent->_right = cur;
    else
        parent->_left = cur;
    cur->_parent = parent;
    
    //...
}

更新平衡因子

首先要明确一点，一个结点的平衡因子由子树的高度差决定，也就是说，子树的高度变化只会影响祖先的平衡因子，对堂兄弟等结点没有影响。

当你找到要插入的位置时，该位置的父结点平衡因子可能有三种情况：-1、0、1，这说明该结点一定只有 0 或 1 个孩子（因为至少留有一个要插入的位置），且高度为 1 或 2（叶子结点高度按 1 算）。
若插入到左边，则父结点平衡因子 -1，插入到右边，父结点平衡因子 +1
插入后，如果父结点的平衡因子变为 0，说明整棵树的高度没有改变，其上的各个祖先结点的平衡因子也就不需要更新
插入后，如果父结点的平衡因子变为 -1 或 1，说明该子树的高度发生了改变，需要继续向上调整各个祖先结点的平衡因子。

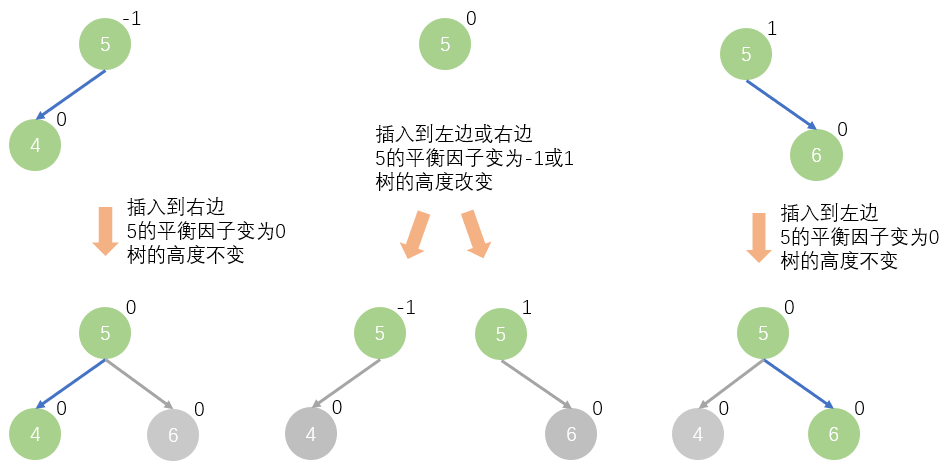
更新平衡因子

更新后的平衡因子为-1、0、1都属于正常，不用调整，如果为-2、2，说明子树不平衡，需要调整，如果绝对值大于2，说明程序出错了，不满足AVL树的条件。

    //...

    // 更新平衡因子
    while (parent) // 最远更新到根
    {
        if (cur == parent->_right)
        {
            ++parent->_bf;
        }
        else
        {
            --parent->_bf;
        }
        // 是否继续更新
        if (parent->_bf == 0)// 为0，更新结束
        {
            break;
        }
        else if (parent->_bf == 1 || parent->_bf == -1)
        {
            cur = cur->_parent;
            parent = parent->_parent;
        }
        else if (parent->_bf == 2 || parent->_bf == -2)
        {
            // 子树不平衡，需要旋转处理

        }
        else
        {
            // 插入前就不满足AVL树的条件，程序出错
            assert(false);
        }
    }
    return true;
}

旋转

对于不平衡的树，我们通过旋转来调整

调整原则：

保持搜索树的规则
子树变平衡

根据结点插入位置的不同，AVL树的旋转分为四种：

新结点插入在其较高右子树的右侧——右右：左旋

下图是一个抽象图，绿三角表示任意的高度相等的AVL树

具体旋转步骤为，将 subRL 变为 parent 的右子树，然后 parent 成为 subR 的左子树

并且旋转完成后，整棵树的高度又回到插入元素之前，也就不需要继续向上调整平衡因子了。

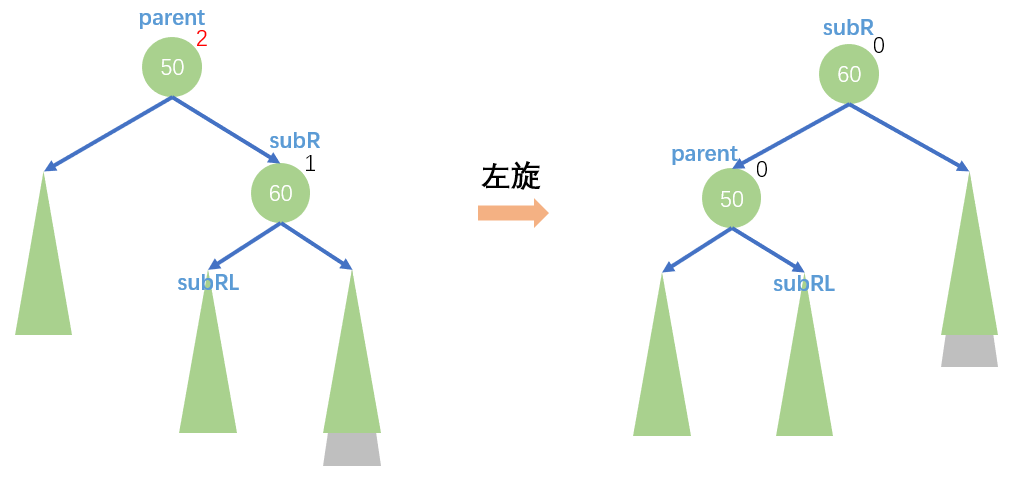
写代码时要注意这是三叉链表，需要考虑结点的 _parent 指针。

private:
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL) subRL->_parent = parent; // subRL有可能是空树，需要if判断

		Node* ppNode = parent->_parent; // 提前记录祖先，后面用来连接新的parent
		subR->_left = parent;
		parent->_parent = subR;

		if (parent == _root) // 如果parent就是根结点，那么新的根是subR
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else // 否则需要祖先来连接新的parent(即subR)，注意判断左右
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subR;
			}
			else
			{
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}
        
		// 更新平衡因子
		parent->_bf = 0;
		subR->_bf = 0;
	}

新结点插入在其较高左子树的左侧——左左：右旋

思路和左旋差不多：

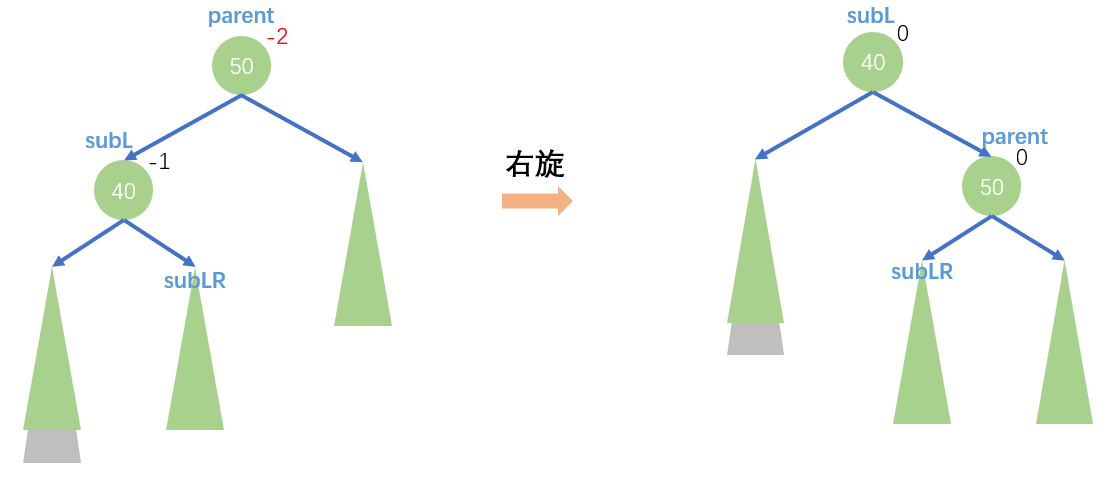
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR) subLR->_parent = parent;

		Node* ppNode = parent->_parent;
		subL->_right = parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subL;
			}
			else
			{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
		parent->_bf = 0;
		subL->_bf = 0;
	}

新结点插入在较高左子树的右侧——左右：先左旋再右旋

如下图，深绿色三角表示任意高度相等的AVL树，浅绿色三角比深绿色三角高度低1层

这种情况下又分三个小情况

新结点插入在 subLR 的左子树，subLR 的平衡因子变为 -1
新结点插入在 subLR 的右子树，subLR 的平衡因子变为 1
subLR 就是新结点，（即深绿色三角高度为 0，浅绿色三角不存在），subLR 的平衡因子为 0

不管是哪种情况，旋转方式都一样，先对 subL 子树左旋，然后对 parent 右旋。

旋转后的高度和插入前相等，也不用继续向上更新祖先的平衡因子。

旋转后需要更新平衡因子，对应旋转前 subLR 的平衡因子，旋转后的平衡因子分别为：

旋转前 sunLR：-1；旋转后 parent：1，subL：0，subLR：0
旋转前 subLR：1；旋转后 parent：0，subL：-1，subLR：0
旋转前 subLR：0；旋转后 parent：0，subL：0，subLR：0

左右旋

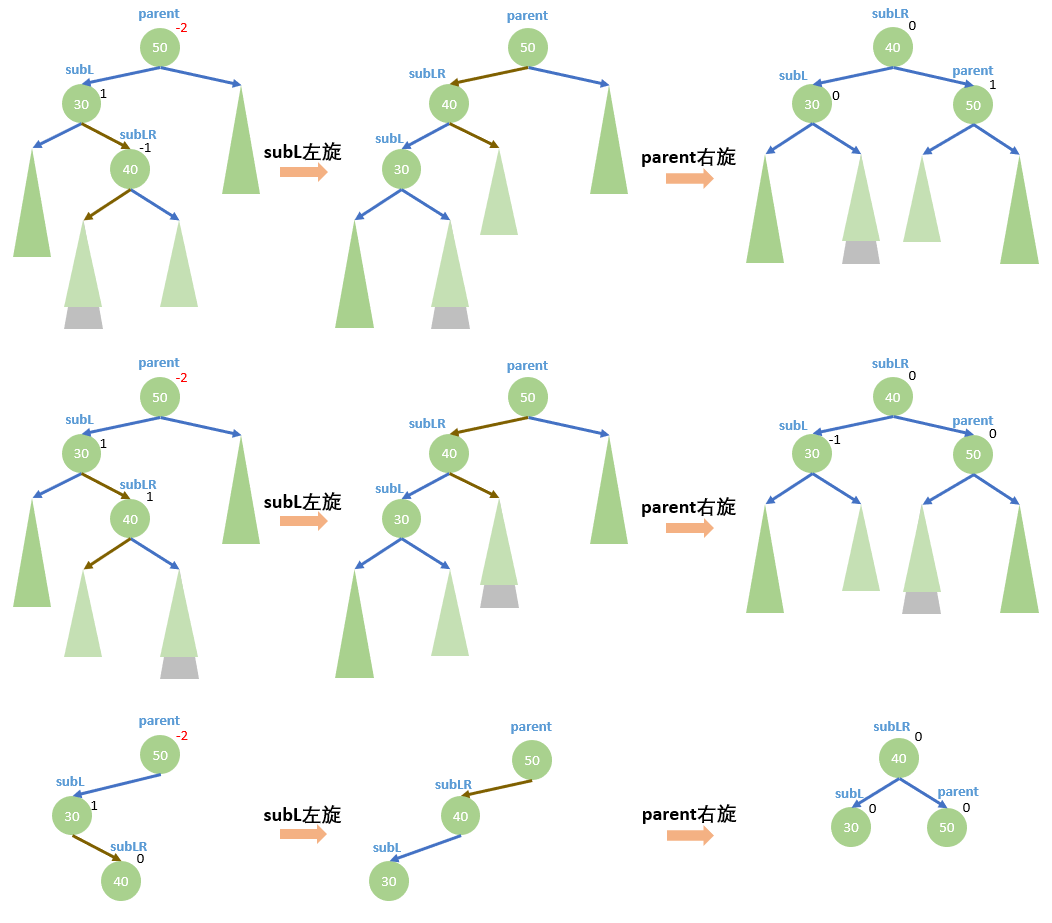
代码其实很简单，因为可以复用已经写好的左旋和右旋。

	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left; // 提前记录subL和subLR以及subLR的bf，方便后面更新平衡因子
		Node* subLR = subL->_right;
		int bf = subLR->_bf;
		// 复用左旋和右旋
		RotateL(parent->_left); 
		RotateR(parent);
		// 更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

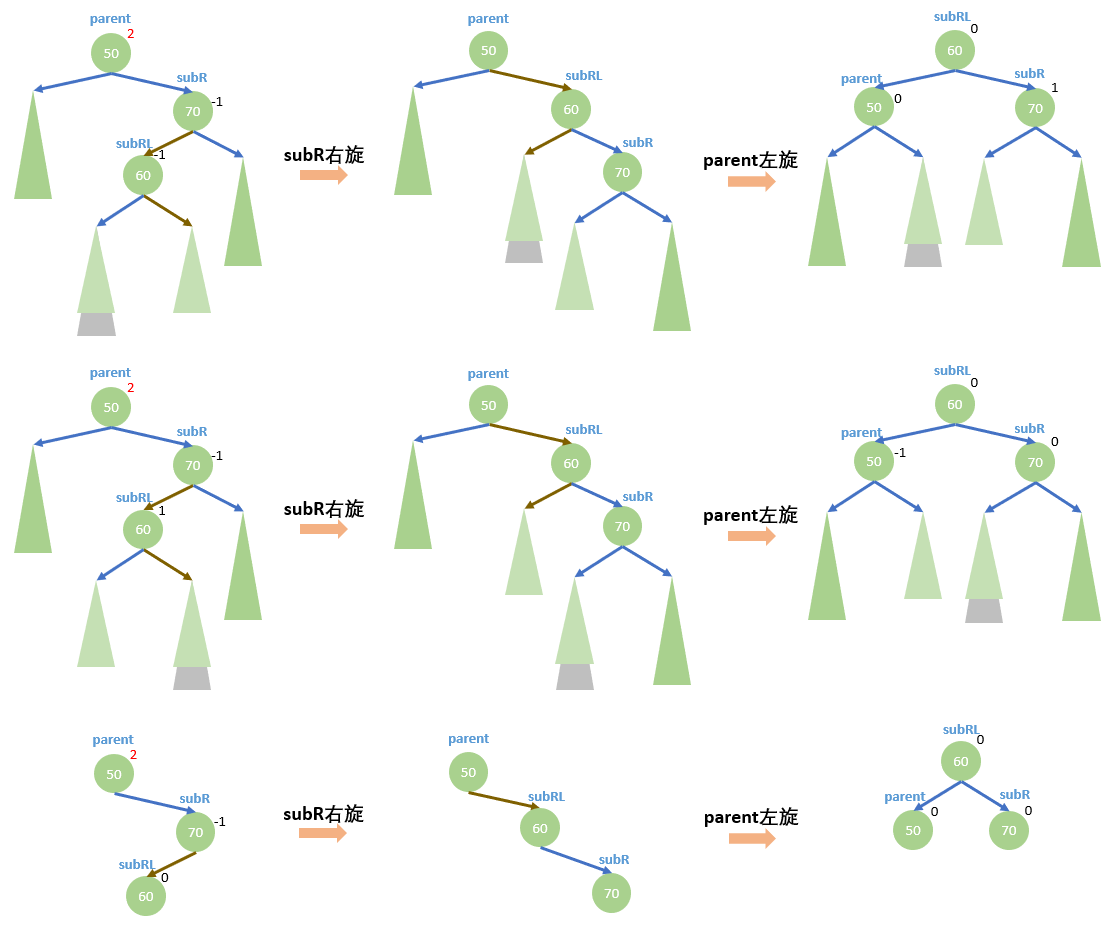
新结点插入在较高右子树的左侧——右左：先右旋再左旋

旋转后需要更新平衡因子，对应旋转前 subRL 的平衡因子，旋转后的平衡因子分别为：

旋转前 sunRL：-1；旋转后 parent：0，subR：1，sunRL：0
旋转前 sunRL：1；旋转后 parent：-1，subR：0，sunRL：0
旋转前 sunRL：0；旋转后 parent：0，subR：0，sunRL：0

右左旋

	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right; // 提前记录subR和subRL以及subRL的bf，方便后面更新平衡因子
		Node* subRL = subR->_left;
		int bf = subRL->_bf;
		// 复用右旋和左旋
		RotateR(parent->_right);
		RotateL(parent);
		// 更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
			subRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

到此为止，四种旋转调整的实现已经完成了，最后判断一下什么情况下用什么旋转：

parent的平衡因子为 2，cur的平衡因子为 1，右右，需要左旋
parent的平衡因子为 -2，cur的平衡因子为 -1，左左，需要右旋
parent的平衡因子为 -2，cur的平衡因子为 1，左右，需要左右双旋
parent的平衡因子为 2，cur的平衡因子为 -1，右左，需要右左双旋

旋完直接 break 不用继续往上更新平衡因子。

//...

else if (parent->_bf == 2 || parent->_bf == -2)
{
    // 子树不平衡，需要旋转处理
    if (parent->_bf == 2 && cur->_bf == 1) // 右右——左旋
    {
        RotateL(parent);
    }
    else if (parent->_bf == -2 && cur->_bf == -1) // 左左——右旋
    {
        RotateR(parent);
    }
    else if (parent->_bf == -2 && cur->_bf == 1) // 左右——左右旋
    {
        RotateLR(parent);
    }
    else if (parent->_bf == 2 && cur->_bf == -1) // 右左——右左旋
    {
        RotateRL(parent);
    }
    break;
}

//...

这里我们可以验证写出来的是不是AVL树，

通过层序遍历直观感受AVL树的长相。
通过逻辑检查是否符合AVL树的规则。

public:
	void LevelOrder()
	{
		queue<Node*> que;
		if (_root != NULL) que.push(_root);
		while (!que.empty())
		{
			int size = que.size();
			for (int i = 0; i < size; i++)
			{
				Node* node = que.front();
				que.pop();
				cout << node->_kv.first << ' ';
				if (node->_left) que.push(node->_left);
				if (node->_right) que.push(node->_right);
			}
			cout << endl;
		}
	}

	bool IsAVLTree()
	{
		return _IsAVLTree(_root);
	}

private:
	bool _IsAVLTree(Node* root)
	{
		if (root == nullptr) return true; // 空树也是AVL树
		// 递归获得左右子树的高度
		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		int diff = rightHeight - leftHeight;
		if (abs(diff) > 1)	// 直接判断高度差是否符合要求
		{
			cout << root->_kv.first << "结点左右子树不平衡";
			return false;
		}
		if (diff != root->_bf) // 判断平衡因子是否符合实际
		{
			cout << root->_kv.first << "结点平衡因子不符合实际";
			return false;
		}

		return _IsAVLTree(root->_left) && _IsAVLTree(root->_right); // 递归检查各个结点
	}

	int _Height(Node* root)
	{
		if (root == nullptr) return 0;
		int leftDepth = _Height(root->_left);
		int rightDepth = _Height(root->_right);
		return  leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
	}

插入随机值，然后检查：

void test2()
{
	const size_t N = 100;
	vector<int> v;
	v.reserve(N);
	for (size_t i = 0; i < N; ++i)
	{
		v.push_back(rand());
	}

	AVLTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, 0));
	}
	t.LevelOrder();
	cout << endl;
	cout << t.IsAVLTree();
}

顺序插入检查：

结果完美符合预期！

完整代码

#pragma once
#include <iostream>
#include <cassert>
#include <vector>
#include <queue>
using namespace std;

template<class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	// 右子树-左子树高度差
	int _bf;	// balance factor

	AVLTreeNode(const pair<K, V>& kv)
		: _kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};

template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_bf = 0;
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
			parent->_right = cur;
		else
			parent->_left = cur;
		cur->_parent = parent;

		// 更新平衡因子
		while (parent) // 最远更新到根
		{
			if (cur == parent->_right)
			{
				++parent->_bf;
			}
			else
			{
				--parent->_bf;
			}
			// 是否继续更新
			if (parent->_bf == 0)// 为0，更新结束
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				// 子树不平衡，需要旋转处理
				if (parent->_bf == 2 && cur->_bf == 1) // 右右——左旋
				{
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1) // 左左——右旋
				{
					RotateR(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1) // 左右——左右旋
				{
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1) // 右左——右左旋
				{
					RotateRL(parent);
				}
				break;
			}
			else
			{
				// 插入前就不满足AVL树的条件，程序出错
				assert(false);
			}
		}
		return true;
	}

	void LevelOrder()
	{
		queue<Node*> que;
		if (_root != NULL) que.push(_root);
		while (!que.empty())
		{
			int size = que.size();
			for (int i = 0; i < size; i++)
			{
				Node* node = que.front();
				que.pop();
				cout << node->_kv.first << ' ';
				if (node->_left) que.push(node->_left);
				if (node->_right) que.push(node->_right);
			}
			cout << endl;
		}
	}

	bool IsAVLTree()
	{
		return _IsAVLTree(_root);
	}

private:
	bool _IsAVLTree(Node* root)
	{
		if (root == nullptr) return true;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		int diff = rightHeight - leftHeight;
		if (abs(diff) > 1)
		{
			cout << root->_kv.first << "结点左右子树不平衡";
			return false;
		}
		if (diff != root->_bf)
		{
			cout << root->_kv.first << "结点平衡因子不符合实际";
			return false;
		}

		return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);
	}

	int _Height(Node* root)
	{
		if (root == nullptr) return 0;
		int leftDepth = _Height(root->_left);
		int rightDepth = _Height(root->_right);
		return  leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
	}

private:
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL) subRL->_parent = parent; // subRL有可能是空树，需要if判断

		Node* ppNode = parent->_parent; // 提前记录祖先，后面用来连接新的parent
		subR->_left = parent;
		parent->_parent = subR;

		if (parent == _root) // 如果parent就是根结点，那么新的根是subR
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else // 否则需要祖先来连接新的parent(即subR)，注意判断左右
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subR;
			}
			else
			{
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}

		// 更新平衡因子
		parent->_bf = 0;
		subR->_bf = 0;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR) subLR->_parent = parent;

		Node* ppNode = parent->_parent;
		subL->_right = parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subL;
			}
			else
			{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
		parent->_bf = 0;
		subL->_bf = 0;
	}

	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left; // 提前记录subL和subLR以及subLR的bf，方便后面更新平衡因子
		Node* subLR = subL->_right;
		int bf = subLR->_bf;
		// 复用左旋和右旋
		RotateL(parent->_left); 
		RotateR(parent);
		// 更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right; // 提前记录subR和subRL以及subRL的bf，方便后面更新平衡因子
		Node* subRL = subR->_left;
		int bf = subRL->_bf;
		// 复用右旋和左旋
		RotateR(parent->_right);
		RotateL(parent);
		// 更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
			subRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}
private:
	Node* _root = nullptr;
};