?
今天鼠鼠带你玩转二叉树~
你间歇性的努力和蒙混过日子,都是对之前努力的清零!
目录
1.4 已知前序,中序或者已知中序、后序,写出树的前序遍历结果
3.2 判断二叉树是否为平衡二叉树(一个二叉树每个节点?的左右两个子树的高度差的绝对值不超过 1 )
四、利用队列层序遍历树(栈和队列?我写的另一篇博客 讲解队列与栈)
前言
讲二叉树,我们首先了解一下树的相关概念和专有名词。
1.树的概念
树是一种非线性的数据结构,它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。有一个特殊的结点,称为根结点,根节点没有前驱结点除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继因此,树是递归定义的。
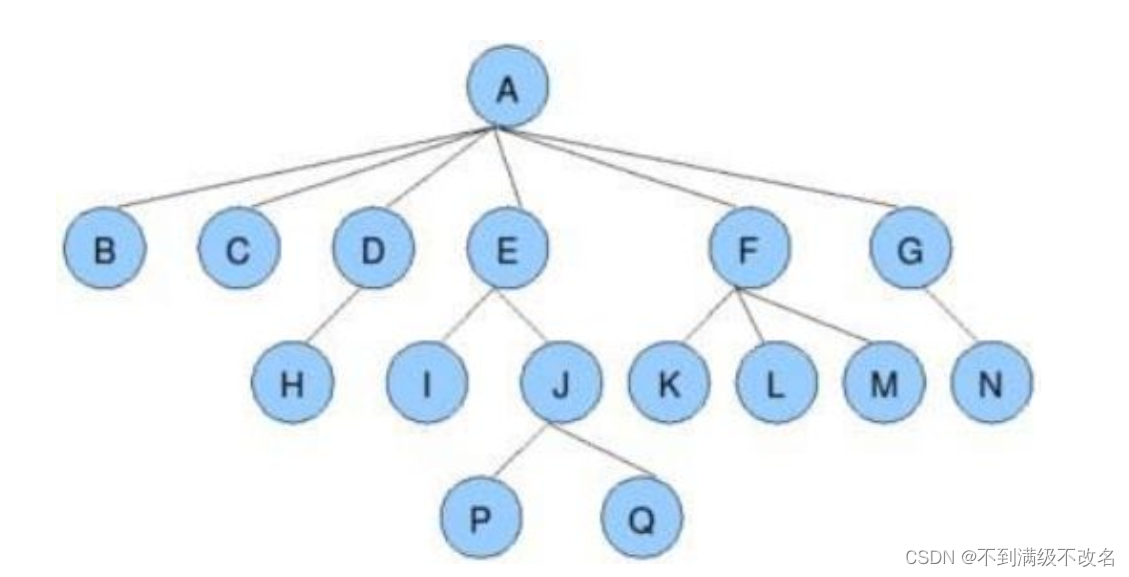
2.树的专有名词
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B
的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节
点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是
一个森林)
一、二叉树是什么?(性质)
1.二叉树的概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子
树和右子树的二叉树组成。
?
2.二叉树的特点:
1. 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
2. 二叉树的子树有左右之分,其子树的次序不能颠倒。
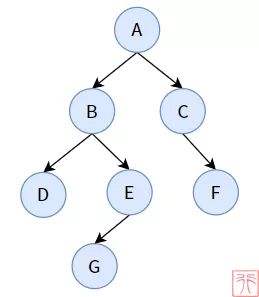
3.特殊的二叉树
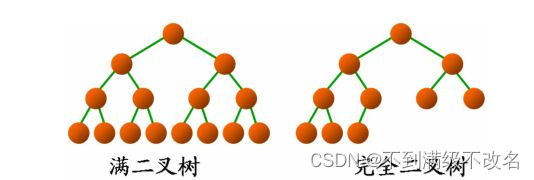
3.1.满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉
树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
3.2.完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对
于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号
从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉
树。
4.二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h- 1.
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2
+1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=LogN
5.存储方式!!!
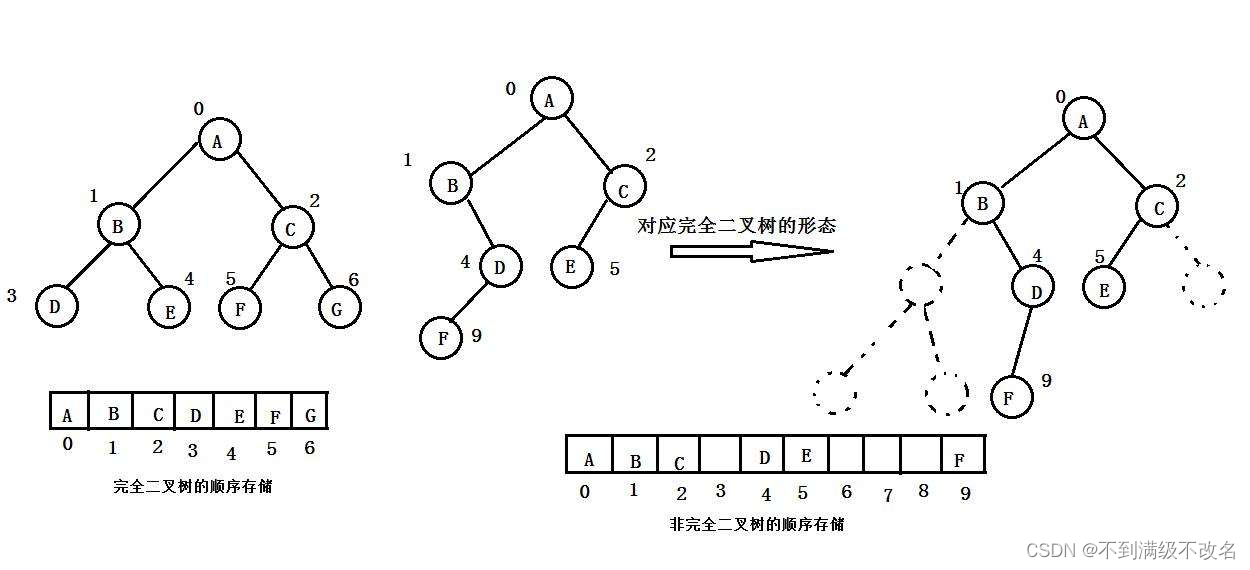
5.1顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树
会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
C语言实现堆?我写的另一篇博客~
5.2 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的
方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩
子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都
是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链
?

二、基本概念题目讲解
Q1.树的概念问题
1.1 在用树表示的目录结构中,从根目录到任何数据文件,有( A)通道
题目内容:
A?.唯一一条? ??B?.二条? ? ?C?.三条? ? ? D?.不一定
解析:树的特点是不相交,所以不可能有多个路径同时到达一个点。
1.2 下列关于树的叙述正确的是( D)
A.树中可以有环
B.树的度是指所有结点中度最小的结点的度
C.树的深度指的是结点数最多的那一层的深度
D.树的根结点是所有结点的祖先结点
1.3?下列关于二叉树的叙述错误的是( A? )
A.二叉树指的是深度为 2 的树
B.一个 n 个结点的二叉树将拥有 n-1 条边
C.一颗深度为 h 的满二叉树拥有 2^h-1 个结点(根结点深度为1)
D.二叉树有二叉链和三叉链两种表示方式
Q2.求叶结点问题
2.1 已知度求未知度
在一颗度为3的树中,度为3的结点有2个,度为2的结点有1个,度为1的结点有2个,则叶子结点有(C)个
A?.4? ? B?.5? ?C?.6? ?D?.7
解析:1.画图求解 2.数学推算?
该树总共有n个节点,则n=n0+n1+n2+n3.?
有n个节点的树的总边数为n-1条.
根据度的定义,总边数与度之间的关系为:n-1=0*n0+1*n1+2*n2+3*n3.
联立两个方程求解,可以得到n0?= n2 + 2n3 + 1,??n0=6
2.2 特殊二叉树求叶节点个数
一颗完全二叉树有1001个结点,其叶子结点的个数是(C )
A.251? ?B.500? ?C.501? ?D.不能确定
解析:设度为0,1,2的结点个数分别为n0,n1,n2。可知n0+n1+n2=1001?
由二叉树性质可知 n0=n2-1,完全二叉树度为1的结点个数非0即1!
∴ n0 + 0 + n2 = 2*n0-1 = 1001 ->? n0 = 501
Q3:深度问题
3.1特殊二叉树深度
有n个元素的完全二叉树的深度是( D? )
A.nlogn? ?B.nlog(n+1)? ?C.logn? ?D.log(n+1)
完全二叉树深度==满二叉树深度 把该二叉树看作满二叉树 利用公式 2的h次方-1=n ->h=log(n+1)
3.2?已知结点个数求深度范围
设根结点的深度为1,则一个拥有n个结点的二叉树的深度一定在(? A )区间内
A.[log(n + 1),n]
B.[logn,n]
C.[log(n + 1),n - 1]
D.[log(n + 1),n + 1]
最大深度: 即每次只有一个节点,次数二叉树的高度为n,为最高的高度
最小深度: 此树为完全二叉树, 如果是完全二叉树
根据二叉树性质,完全二叉树的高低为 h = log(n+1)向上取整
三、用递归实现树的函数
首先先初始化一棵二叉树
typedef char TreeDataType;
typedef struct Tree
{
TreeDataType Data;
struct Tree* Left;
struct Tree* Right;
}tree;
tree* a = (tree*)malloc(sizeof(tree));
a->Data = 'A';
a->Left = NULL;
a->Right = NULL;
tree* b = (tree*)malloc(sizeof(tree));
b->Data = 'B';
b->Left = NULL;
b->Right = NULL;
tree* c = (tree*)malloc(sizeof(tree));
c->Data = 'C';
c->Left = NULL;
c->Right = NULL;
tree* d = (tree*)malloc(sizeof(tree));
d->Data = 'D';
d->Left = NULL;
d->Right = NULL;
tree* e = (tree*)malloc(sizeof(tree));
e->Data = 'E';
e->Left = NULL;
e->Right = NULL;
tree* f = (tree*)malloc(sizeof(tree));
f->Data = 'F';
f->Left = NULL;
f->Right = NULL;
a->Left = b;
a->Right = c;
b->Left = d;
b->Right = e;
c->Left = f;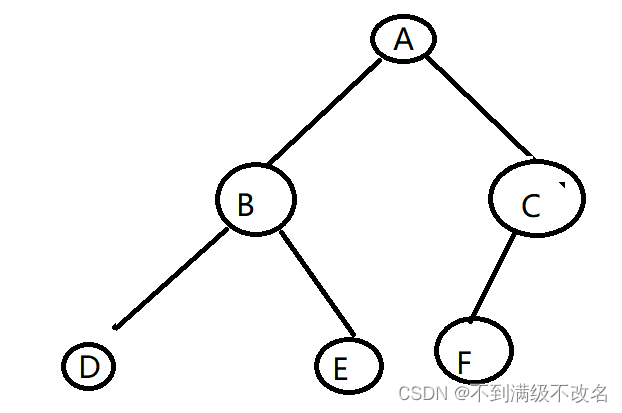
1.树的遍历(打印存储的数据)
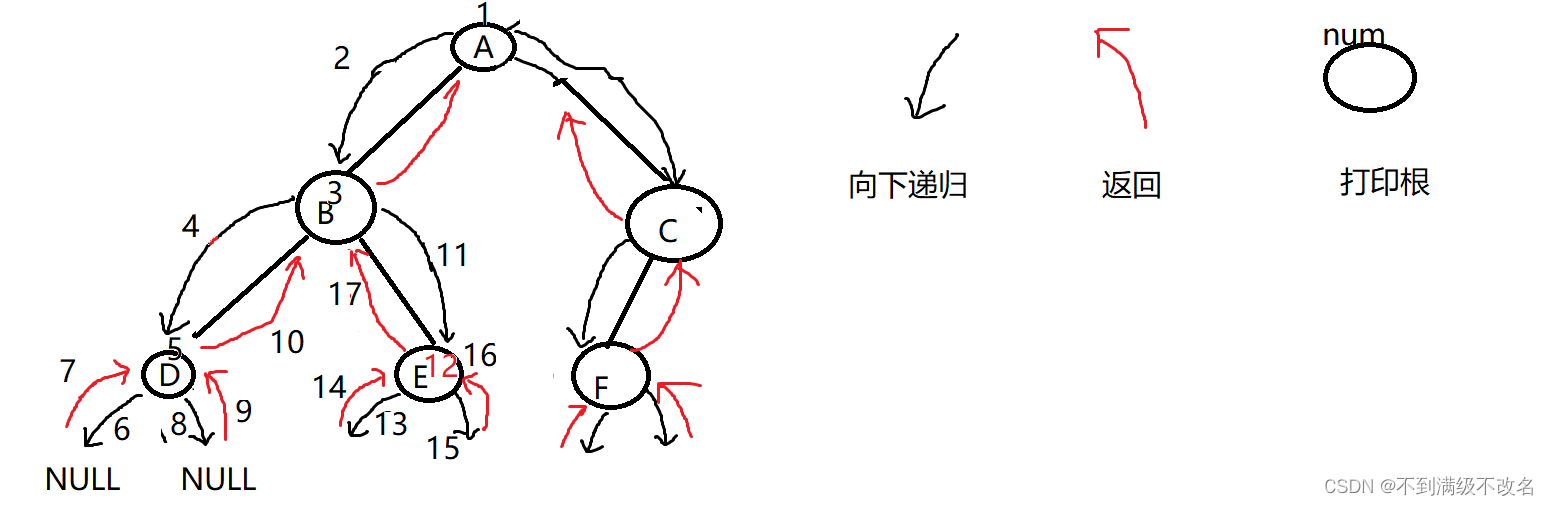
1.1 前序遍历
遵循先根结点,后左子树,右子树的顺序打印Data
上代码~
void preorder(tree* root)
{
//为空返回
if (root == NULL)
{
printf("NULL ");
return;
}
//先打印根结点
printf("%c ", root->Data);
//后左子树
preorder(root->Left);
//最后右子树
preorder(root->Right);
}

1.2 中序遍历
遵循先左子树 后根 最后右子树
void InfixOrder(tree* root)
{
//为空返回
if (root == NULL)
{
printf("NULL ");
return;
}
//先左子树
InfixOrder(root->Left);
//后打印根
printf("%c ", root->Data);
//最后右子树
InfixOrder(root->Right);
}
?1.3后序遍历
遵循先左子树 后右子树 最后根
void BehindOrder(tree* root)
{
//为空返回
if (root == NULL)
{
printf("NULL ");
return;
}
//先左子树
BehindOrder(root->Left);
//后右子树
BehindOrder(root->Right);
//最后打印根
printf("%c ", root->Data);
}
1.4 已知前序,中序或者已知中序、后序,写出树的前序遍历结果
已知某二叉树的中序遍历序列为JGDHKBAELIMCF,后序遍历序列为JGKHDBLMIEFCA,则其前序遍历序列为(B )
A?.ABDGHJKCEFILM
B?.ABDGJHKCEILMF
C?.ABDHKGJCEILMF
D?.ABDGJHKCEIMLF
解析:由后序遍历确定子树的根,后序遍历从后向前看,最后一个元素为根,和前序遍历刚好相反,从后向前看后序遍历,应该是根,右,左,根据中序遍历确定子树的左右区间。
故:根为: A
A的左子树:JGDHKB???????A的右子树:ELIMCF
A的左子树的根:B????????A的右子树的根:C
B的左子树:JGDHK??B的右子树:空??C的左子树:ELIM?C的右子树:F
B的左子树的根:D?????????C的左子树根:E
D的左子树的根:G D的右子树的根:H??E的右子树的根:I
故树的结构为:
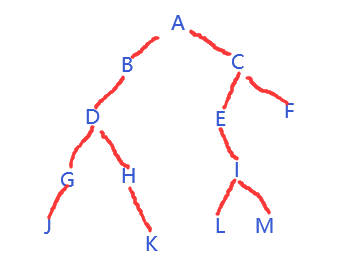
1.5已知树前序遍历结果,求树右多少种结构
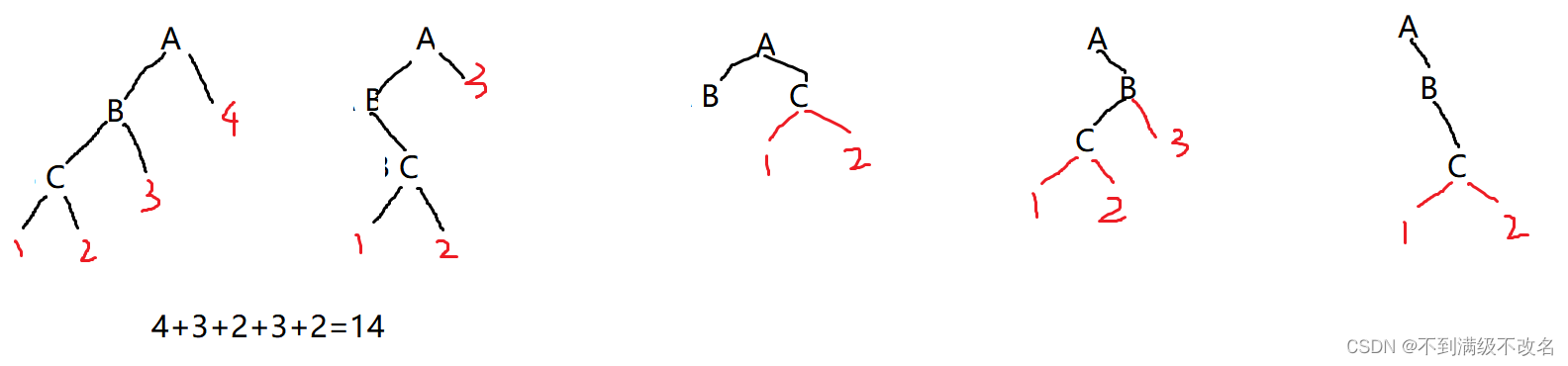
如果一颗二叉树的前序遍历的结果是ABCD,则满足条件的不同的二叉树有( B)种
A?.13? ?B?.14? ?C?.15? ?D?.16
解析:用定三移一法!先将ABC的位置确定,然后移动D的位置
1.6通过先序遍历结果构建一棵树,再中序遍历打印结点数据
题目:编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
解析:通过数组我们拿到了字符串,那么我们可以利用递归的方式去构造这棵树。非'#'我们开辟结点存字符并递归其左右子树,遇到’#‘返回空,最后返回结点地址(这句话这个地址只有头结点返回有意义)
易错点:数组下标没调用一次函数,就必须++一次。答案中我们传参传的是i的地址,如果不传地址,后果就是当你先给左子树递归调用的完成的时候,虽然i++了,但是此时i是局部变量,返回时就销毁了,你再一次调用右子树的时候i依旧不变,下一个数据会覆盖前一个位置。
以"AB##C##"为例

#include<stdio.h>
#include<stdlib.h>
typedef struct BTNode
{
struct BTNode*left;
struct BTNode*right;
char val;
}BTNode;
BTNode* CreatTree(int*a,int*pi)
{
if(a[*pi]=='#')
{
(*pi)++;
return NULL;
}
BTNode* newnode=(BTNode*)malloc(sizeof(BTNode));
newnode->val=a[*pi];
(*pi)++;
newnode->left=CreatTree(a,pi);
newnode->right=CreatTree(a, pi);
return newnode;
}
void MiddleOrder(BTNode*root)
{
if(root==NULL)
return;
MiddleOrder(root->left);
printf("%c ",root->val);
MiddleOrder(root->right);
}
int main()
{
char arr[101];
scanf("%s",arr);
int i=0;
BTNode*root=CreatTree(arr,&i);
MiddleOrder(root);
return 0;
}2.求结点个数问题
2.1 求树结点个数
int NumTreeNode(tree* root)
{
//遇空返回0
if (root == NULL) {
return 0;
}
// 左子树结点+右子树结点+本身
return NumTreeNode(root->Left) + NumTreeNode(root->Right) + 1;
}2.2 求叶节点个数
int LeafSize(tree* root)
{
//遇空返回0
if (root==NULL) {
return 0;
}
//左右都为空返回1,否则继续递归左右子树
return root->Left || root->Right ? LeafSize(root->Left) + LeafSize(root->Right) : 1;
}2.3 求第K层结点个数
int TreeLevelKSize(tree* root, int k)
{
assert(k > 0);
int level = 1;
//未达到指定层,则继续左右子树向下递归
if (level < k)
{
return TreeLevelKSize(root->Left, k-1)+ TreeLevelKSize(root->Right, k-1);
}
//达到指定层,非空返回1,为空返回0
if (level == k)
{
if (root != NULL)
return 1;
else {
return 0;
}
}
}3.深度问题
3.1 求最大深度
int MaxDepth(tree* root)
{
if (root==NULL) {
return 0;
}
int Leftdepth = MaxDepth(root->Left);
int Rightdepth = MaxDepth(root->Right);
return Leftdepth > Rightdepth ? Leftdepth + 1 : Rightdepth + 1;
}3.2 判断二叉树是否为平衡二叉树(一个二叉树每个节点?的左右两个子树的高度差的绝对值不超过 1 )
int Maxdepth(struct TreeNode* root)
{
if(root==NULL)
return 0;
int leftdepth=Maxdepth(root->left);
int rightdepth=Maxdepth(root->right);
return leftdepth>rightdepth?leftdepth+1:rightdepth+1;
}
bool isBalanced(struct TreeNode* root){
//遍历到空说明前面树都满足条件了,返回真
if(root==NULL)
return true;
//判断每一个结点的左右子树最大深度相差是否满足条件,
//有一个不满足返回false停止递归,满足继续递归
int Leftdepth = Maxdepth(root->left);
int Rightdepth = Maxdepth(root->right);
return abs(Leftdepth - Rightdepth) < 2 &&
isBalanced(root->left) &&
isBalanced(root->right);
}4.树的关系问题
4.1 翻转二叉树
题目:
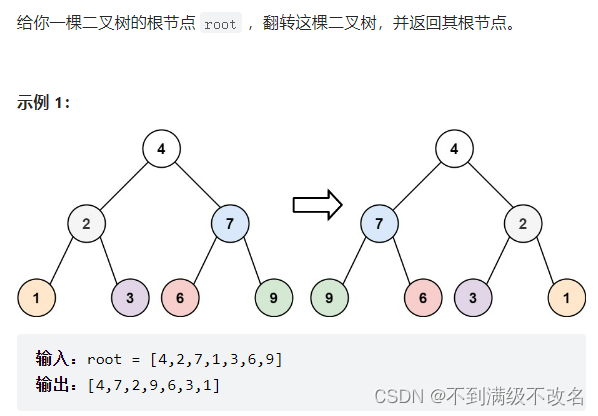
struct TreeNode* invertTree(struct TreeNode* root){
//遇到空结点或者左右子树都为空,直接返回
if(root==NULL||(root->left==NULL&&root->right==NULL))
return root;
//交换
struct TreeNode* tmp=root->left;
root->left=root->right;
root->right=tmp;
//递归
invertTree(root->left);
invertTree(root->right);
//返回
return root;
}4.2 检查两颗树是否相同
题目:

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//都为空是真
if(p==NULL&&q==NULL)
return true;
//其中一个为空,另一个不为空或者都不为空却值不同为假
if(p==NULL||q==NULL||p->val!=q->val)
return false;
//递归左右子树 左右都为真返回真
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}4.3 判断树是否为对称二叉树

思路:先翻转根的左子树,然后判断左右子树是否是相同的树?,这就结合了前两题!
//翻转左子树
void invertTree(struct TreeNode* root){
if(root==NULL||(root->left==NULL&&root->right==NULL))
return;
struct TreeNode* tmp=root->left;
root->left=root->right;
root->right=tmp;
invertTree(root->left);
invertTree(root->right);
}
//判断左右子树是否是相同的树
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL||p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
bool isSymmetric(struct TreeNode* root){
invertTree(root->left);
return isSameTree(root->left,root->right);
}4.4 判断一棵树子树是否与另一棵树相同
题目:

//判断两棵树是否相同
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL||p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
//找到最后说明之前都没有,返回假
if(root==NULL)
return false;
//判断两棵树是否相同,为真返回真
if(isSameTree(root,subRoot))
return true;
//只要找到了左右有一边找到了就可以返回真
return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}四、利用队列层序遍历树(栈和队列?我写的另一篇博客 讲解队列与栈)
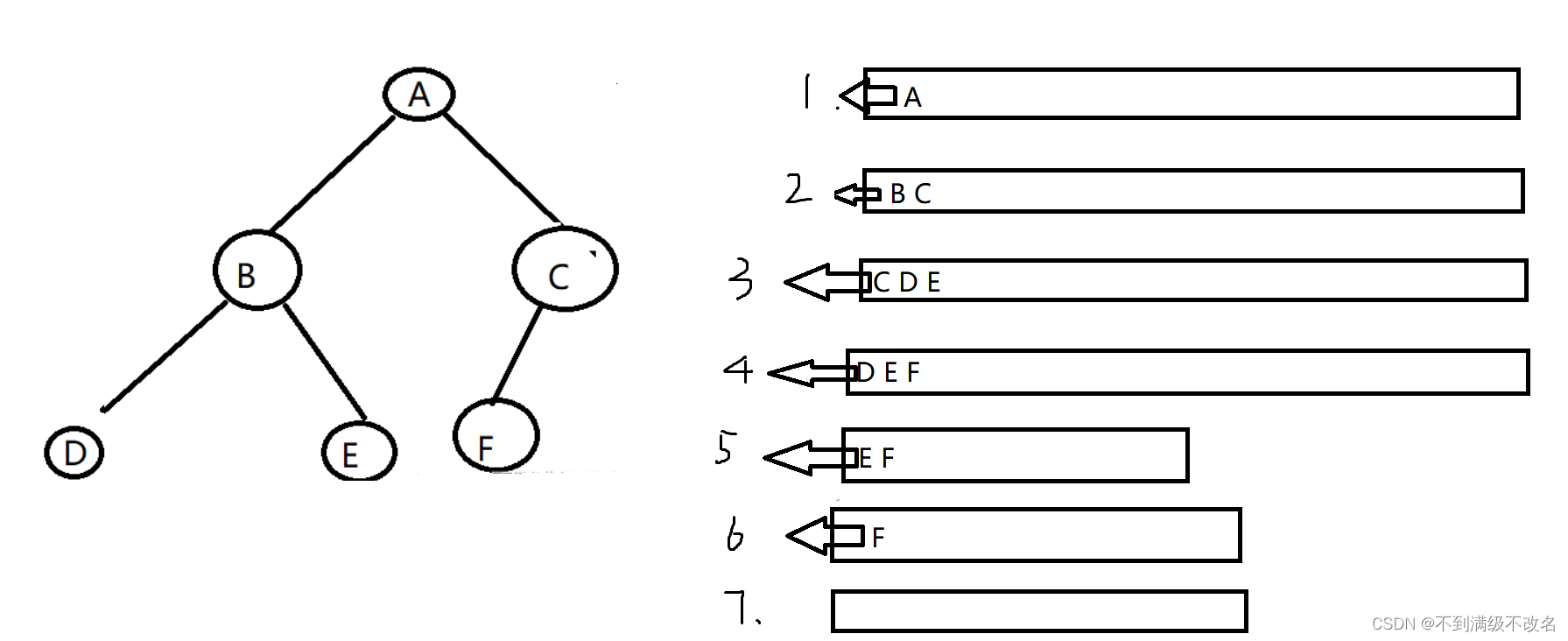
1.层序遍历
void LevelOrderTraverse(tree* root)
{
printf("层序遍历:");
//定义并初始化队列
Queue q;
QueueInit(&q);
//根入队列
if (root) {
QueuePush(&q, root);
}
while (!QueueEmpty(&q)) {//非空继续遍历
QDataType Front= QueueFront(&q);//取队头
printf("%c ", Front->Data);
QueuePop(&q);//出队
//判断子节点是否为空,非空入队
if (Front->Left) {
QueuePush(&q, Front->Left);
}
if (Front->Right) {
QueuePush(&q,Front->Right);
}
}
printf("\n");
}
?
2.利用层序遍历判断一棵树是否为完全二叉树
完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对
于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号
从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉
树。
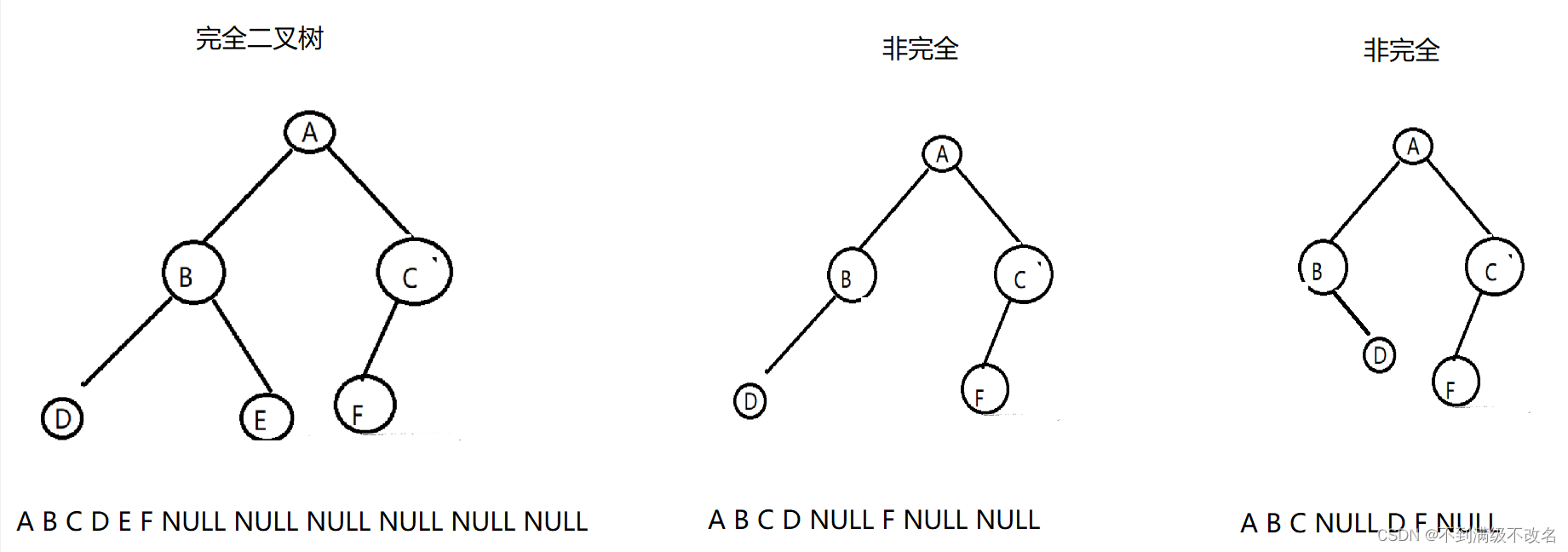
?通过上图,我们如果把NULL加入到队列中,通过比对完全与非完全不同处,和非完全相同处,我们可以发现完全二叉树NULL后面不会再次出现字符!而非完全NULL后面一定会再次出现字符!
从而我们可以通过判断NULL后面是否出现字符来判断是否为完全二叉树!
此时有人可能会有一种问题?就是有没有可能就是上图中的D先出入了两个NULL,而没轮到F入从而导致后面才入F,NULL后面出现字符的情况?
答案是不可能的,因为层序遍历的特点是一层层的遍历,遍历一层的时候一定会把下一层的入队。所以D E 入队了,那么F 一定也会在B C这一层遍历完前入队的,不会遍历到D那一层还没入队。
bool BinaryTreeComplete(tree* root)
{
assert(root);
//1.建队列,初始化
Queue q;
QueueInit(&q);
//2.入头节点
if (root) {
QueuePush(&q, root);
}
//3.队列不为空就继续出入,当遇到NULL停止循环
while (!QueueEmpty(&q)) {
QDataType Front = QueueFront(&q);//取队头
if (Front == NULL)
{
break;
}
QueuePop(&q);//出队
QueuePush(&q, Front->Left);
QueuePush(&q, Front->Right);
}
//4.判断NULL是否出现字符,出现则是非完,没有则是完全,记得销毁队列
while (!QueueEmpty(&q))
{
QDataType Front = QueueFront(&q);
if (Front != NULL)
{
QueueDestory(&q);
return false;
}
QueuePop(&q);//出队
}
QueueDestory(&q);
return true;
}五、总结
? 以上是初阶二叉树的所有整理内容了。二叉树是数据结构比较难的一部分,需要我们静下心来去画图来明白递归问题。希望这篇文章来给你带来一些启发!如果你在阅读的过程中发现了什么问题,也希望您能不吝赐教!最后制作不易,希望大家给个三连~

?
