目录
????????个遍历结果可以确定树的结构，其一必须是中序遍历
4.二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)?
一.二叉搜索数介绍
1.介绍
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
①若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
②若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
③它的左右子树也分别为二叉搜索树
即：
任意一个子树都需要满足，左子树的值<根<右子树的值 就是
二叉搜索数
对二叉搜索树进行中序遍历，一定能够得到一个有序序列
2.时间复杂度：
二叉搜索树最差情况下会退化为单支树，因此：其查找的效率为O(N)，O(N)这个时间复杂度是线性的
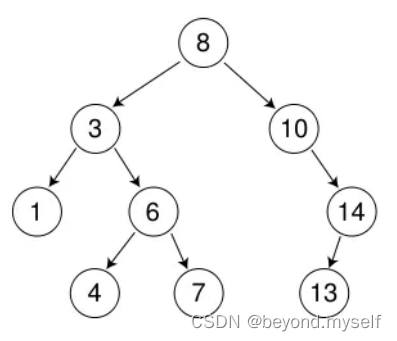
????????个遍历结果可以确定树的结构，其一必须是中序遍历
根据前序遍历和中序遍历，是可以确定一棵树的结构，使用两个遍历结果确定树的结构， 其中有一个遍历结果必须要是中序遍历结果。
解释：
前序：根、左子树、右子树--依次确定根
中序：左子树、根、右子树--划分左右子树区间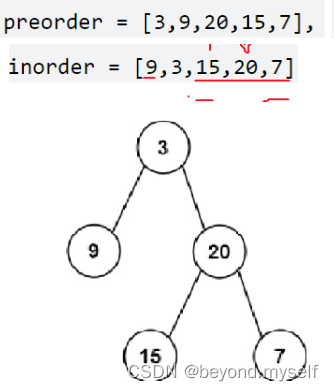
二.模拟实现
第一阶段：增，查?
易错：insert返回类型bool
#pragma once
template<class K>
//struct BinarySearchTreeNode
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
//const Node* Find(const K& key)
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key);
void InOrder()
{
_InOrder(_root);
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
void TestBSTree()
{
BSTree<int> t;
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
t.Insert(16);
t.Insert(9);
t.InOrder();
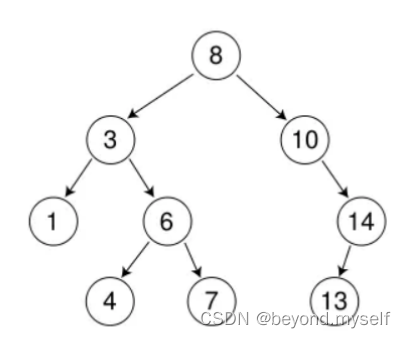
}依次删除7、14、 3、8
7和14属于直接删除的场景
3、8属于需要替换法进行删除的场景
两个孩子没办法给父亲，父亲养不了。找个人替代我养孩子
这个人是：左子树的最大值节点，或者右子树的最小值节点
阶段二：非递归版本-增，删，赋值运算符重载，拷贝构造，析构
问题：FindR为什么要套一层
易错：非递归Erase最后一个if条件if (minParent->_left == minRight)写错，拷贝构造不会写，拷贝函数CopyTree是递归不好写
#pragma once
template<class K>
//struct BinarySearchTreeNode
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
private:
void DestoryTree(Node* root)
{
if (root == nullptr)
return;
DestoryTree(root->_left);
DestoryTree(root->_right);
delete root;
}
Node* CopyTree(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyNode = new Node(root->_key);
copyNode->_left = CopyTree(root->_left);
copyNode->_right = CopyTree(root->_right);
return copyNode;
}
public:
// 强制编译器自己生成构造
// C++11
BSTree() = default; //默认构造很好用，但是拷贝构造也是构造函数，就不会自动生成构造函数
BSTree(const BSTree<K>& t) //拷贝构造
{
_root = CopyTree(t._root);
}
// t1 = t2
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
DestoryTree(_root);
_root = nullptr;
}
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
//const Node* Find(const K& key)
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 一个孩子--左为空 or 右为空
// 两个孩子 -- 替换法
if (cur->_left == nullptr)
{
//if (parent == nullptr)
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
//if (parent == nullptr)
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else // 两个孩子都不为空
{
// 右子树的最小节点替代
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
swap(minRight->_key, cur->_key);
//cur->_key = minRight->_key;
if (minParent->_left == minRight)
{
minParent->_left = minRight->_right;
}
else
{
minParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
///
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
bool _EraseR(Node*& root, const K& key)
//key是10时，root是8的右孩子这个指针的别名，同时指向10
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
Node* del = root;
// 删除
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
swap(root->_key, minRight->_key);
return _EraseR(root->_right, key);
}
delete del;
return true;
}
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
return _InsertR(root->_right, key);
else if (root->_key > key)
return _InsertR(root->_left, key);
else
return false;
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
void TestBSTree1()
{
BSTree<int> t;
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
t.Insert(16);
t.Insert(9);
t.InOrder();
}
void TestBSTree2()
{
BSTree<int> t;
int a[] = { 8, 7, 9, 12, 5, 19, 20, 30,7,12 };
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
}
void TestBSTree3()
{
BSTree<int> t;
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
t.Erase(3);
t.Erase(8);
t.InOrder();
t.Erase(14);
t.Erase(7);
t.InOrder();
for (auto e : a)
{
t.Erase(e);
}
t.InOrder();
}
void TestBSTree4()
{
BSTree<int> t;
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
BSTree<int> copy = t;
copy.InOrder();
}
void TestBSTree5()
{
BSTree<int> t;
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.InsertR(e);
}
t.InOrder();
t.InsertR(9);
BSTree<int> copy = t;
copy.InOrder();
}
void TestBSTree6()
{
BSTree<int> t;
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.InsertR(e);
}
t.InOrder();
t.EraseR(3);
t.EraseR(8);
t.InOrder();
t.EraseR(14);
t.EraseR(7);
t.InOrder();
for (auto e : a)
{
t.EraseR(e);
}
t.InOrder();
}三.二叉搜索树的应用
1. K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到
的值。（K-set）
比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：
以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。
2. KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方
式在现实生活中非常常见：
比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英
文单词与其对应的中文<word, chinese>就构成一种键值对；
再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出
现次数就是<word, count>就构成一种键值对
（KV-map）
namespace key_value
{
#pragma once
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
const K _key;
V _value;
BSTreeNode(const K& key, const V& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
void InOrder()
{
_InOrder(_root);
cout << endl;
}
///
Node* FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key, const V& value)
{
return _InsertR(_root, key, value);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
Node* del = root;
// 删除
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
swap(root->_key, minRight->_key);
return _EraseR(root->_right, key);
}
delete del;
return true;
}
}
bool _InsertR(Node*& root, const K& key, const V& value)
{
if (root == nullptr)
{
root = new Node(key, value);
return true;
}
if (root->_key < key)
return _InsertR(root->_right, key, value);
else if (root->_key > key)
return _InsertR(root->_left, key, value);
else
return false;
}
Node* _FindR(Node* root, const K& key)
{
if (root == nullptr)
return nullptr;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return root;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
K模型：找对应单词的中文
void TestBSTree1()
{
BSTree<string, string> ECDict;
ECDict.InsertR("root", "根");
ECDict.InsertR("string", "字符串");
ECDict.InsertR("left", "左边");
ECDict.InsertR("insert", "插入");
//...
string str;
while (cin >> str) //while (scanf() != EOF)
{
//BSTreeNode<string, string>* ret = ECDict.FindR(str);
auto ret = ECDict.FindR(str);
if (ret != nullptr)
{
cout << "对应的中文:" << ret->_value << endl;
//ret->_key = "";
ret->_value = "";
}
else
{
cout << "无此单词，请重新输入" << endl;
}
}
}KV模型：记录水果的次数
void TestBSTree2()
{
string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
// 水果出现的次数
BSTree<string, int> countTree;
for (const auto& str : arr)
{
auto ret = countTree.FindR(str);
if (ret == nullptr)
{
countTree.InsertR(str, 1);
}
else
{
ret->_value++; // 修改value
}
}
countTree.InOrder();
}补充：cin中的operator bool
operator bool
上面K模型的 while (cin >> str) ?//while (scanf() != EOF) 能做多组输入原因是因为 cin的istream类型重载了 operator bool
#include<iostream>
using namespace std;
class A
{
public:
explicit A(int a = 0)
:_a(a)
{}
operator bool()
{
if (_a < 10)
{
return true;
}
else
{
return false;
}
}
void Print()
{
cout << _a << endl;
}
void Set(int a)
{
_a = a;
}
private:
int _a;
};
void test()
{
A a;
bool ret = a;
int x;
while (a) //while (a.operator bool())
{
a.Print();
cin >> x;
a.Set(x);
}
}
int main()
{
test();
return 0;
}
?operator int也是可以的
内置类型<--自定义类型
explicit operator int() 会导致隐式类型转换 int y = a;不支持
#include<iostream>
using namespace std;
class A
{
public:
explicit A(int a = 0)
:_a(a)
{}
operator int() //explicit operator int() 会导致隐式类型转换 int y = a;不支持
{
if (_a < 10)
{
return 1;
}
else
{
return 0;
}
}
void Print()
{
cout << _a << endl;
}
void Set(int a)
{
_a = a;
}
private:
int _a;
};
void test()
{
A a;
//int y = a;
int x;
//while (a.operator bool())
while (a)
{
a.Print();
cin >> x;
a.Set(x);
}
}
int main()
{
test();
return 0;
}
四.搜素二叉树题目
1.606. 根据二叉树创建字符串
个人思路写法：
class Solution {
public:
string tree2str(TreeNode* root) {
string str;
if(root==nullptr)
return str;
str+=to_string(root->val);
if(root->left||root->right)
{
str+='(';
str+=tree2str(root->left);
str+=')';
}
if(root->right)
{
str+='(';
str+=tree2str(root->right);
str+=')';
}
return str;
}
};官方写法：
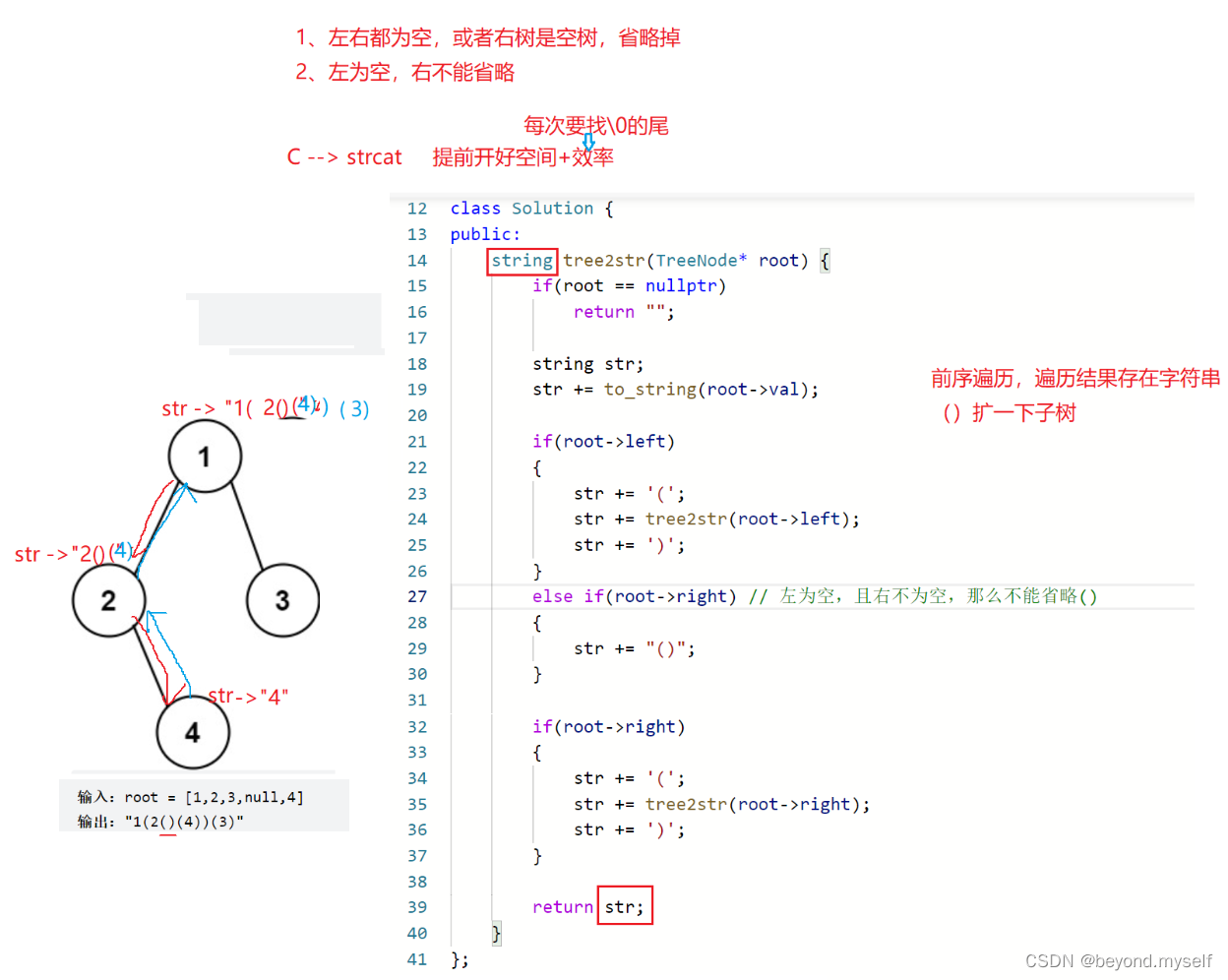
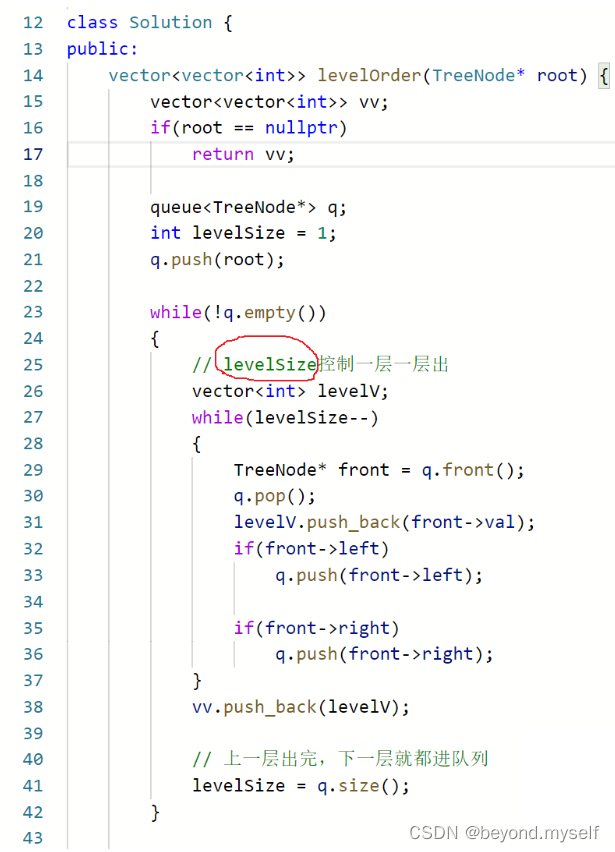
2.?102. 二叉树的层序遍历
利用levelSize 一层一层出
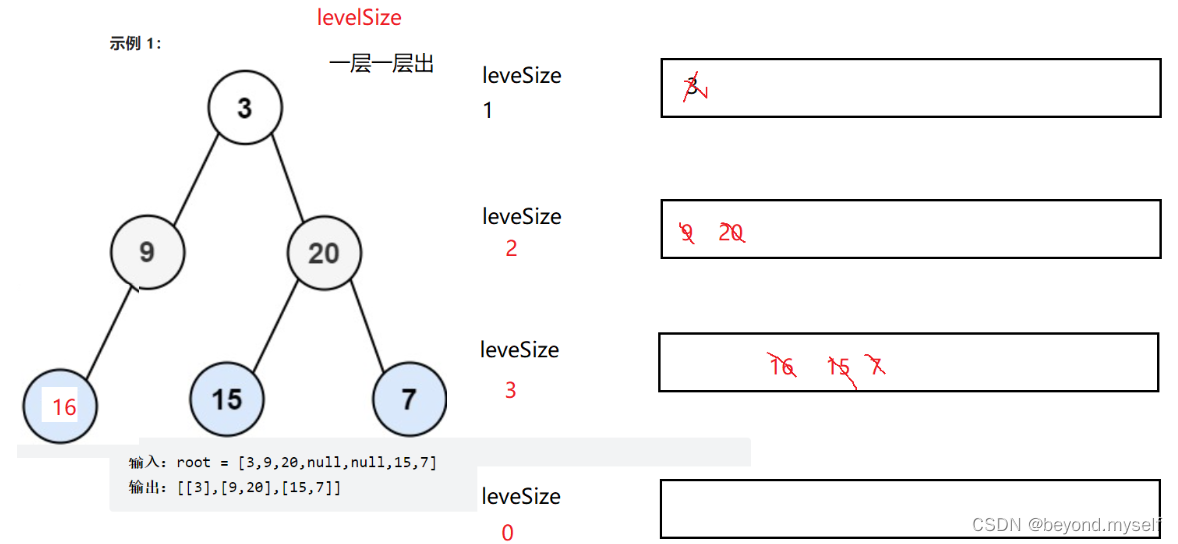
个人手写：
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
if(root==nullptr)
return vv;
queue<TreeNode*> q;
int levelSize=1;
q.push(root);
while(levelSize)
{
vector<int> levelV;
while(levelSize--)
{
TreeNode* front=q.front();
levelV.push_back(front->val);
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
q.pop();
}
vv.push_back(levelV);
levelSize=q.size();
}
return vv;
}
};管方写法：?
3.236. 二叉树的最近公共祖先
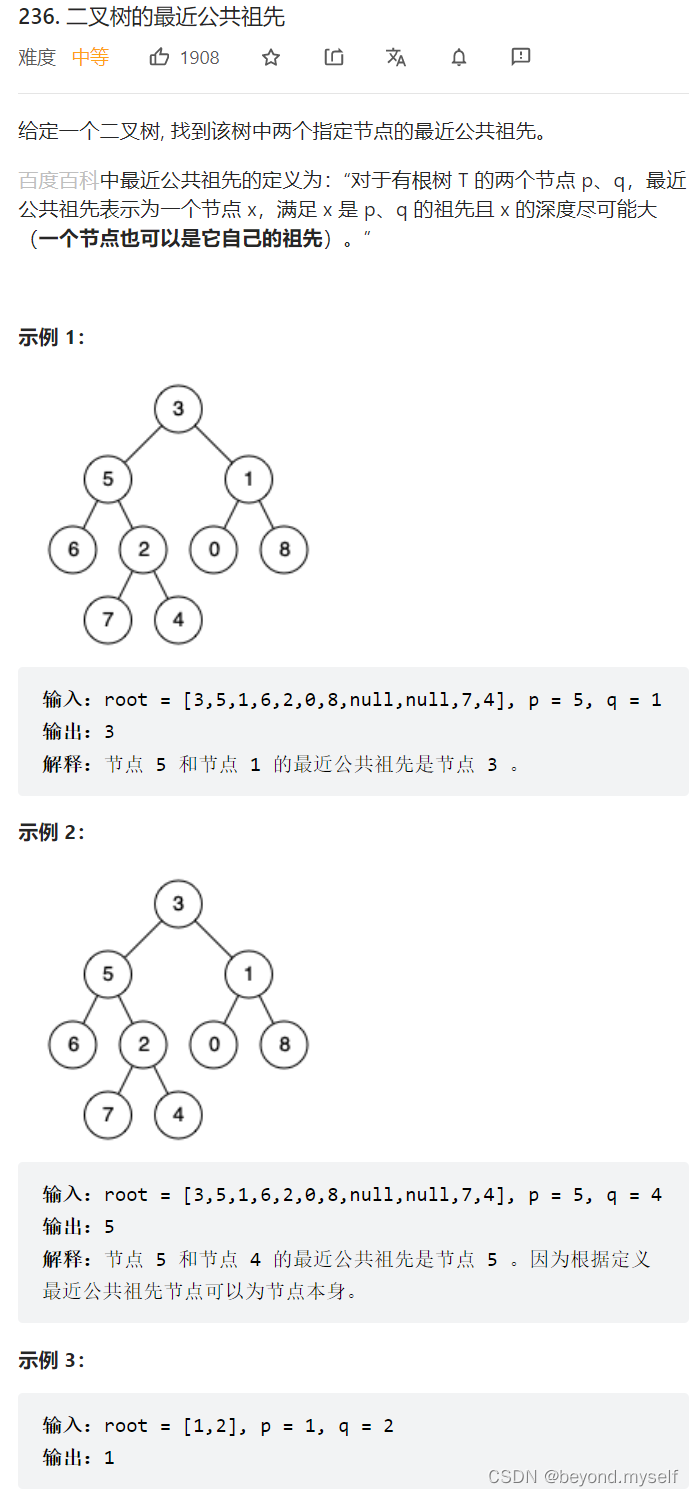
方法一：利用p和q一定在最近公共祖先的两侧来找
个人写法：非递归版本
class Solution {
public:
bool IsInSubTree(TreeNode* tree, TreeNode* x) //看是否在此根节点下
{
if(tree==nullptr)
return false;
if(tree==x) //要比较地址！！
return true;
return IsInSubTree(tree->left, x)||IsInSubTree(tree->right, x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
TreeNode* cur=root;
while(cur)
{
if(p==cur||q==cur)
return cur;
bool pInLeft=IsInSubTree(cur->left, p);
bool pInRight= !pInLeft;
bool qInLeft=IsInSubTree(cur->left, q);
bool qInRight= !qInLeft;
if((pInLeft && qInRight)||(qInLeft && pInRight))
return cur;
else if(pInLeft && qInLeft)
cur=cur->left;
else if(pInRight && qInRight)
cur=cur->right;
}
return nullptr;
}
};官方写法：递归版本
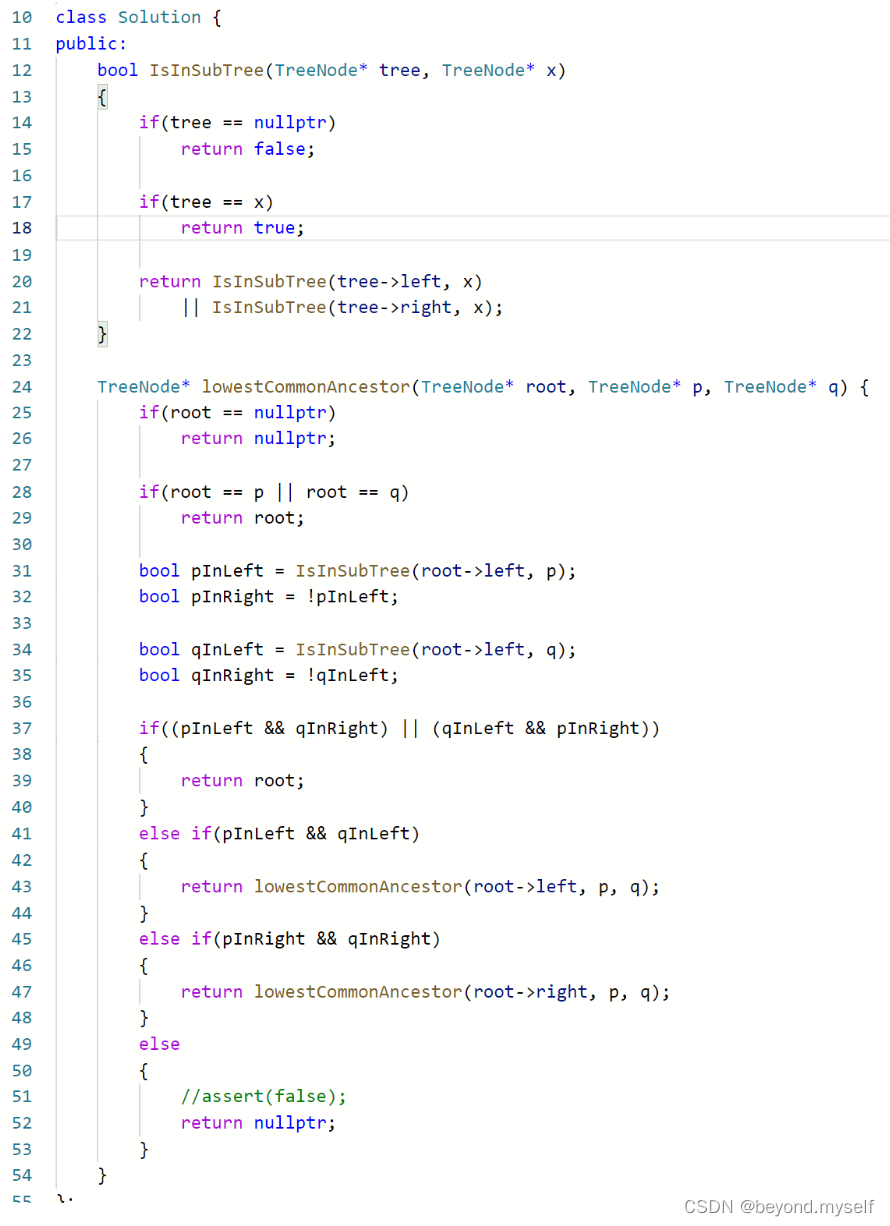
?因为这种写法每走一个节点就要在他的左右子树找p和q节点，N个节点，每个节点最坏找N/2，时间复杂度是O(N2)，所以要用时间复杂度低的方法二。
方法二：找路径交点
根据三叉链（每个节点有左，右，父亲三个指针），可以利用栈记录节点p，q到根的路径，然后找相交路径（先让长的走到和短的一样长，再同时走，相等就是交点，交点就是最近公共祖先）
易错点：FindPath 路径函数(把路径放进栈)递归写法不好写
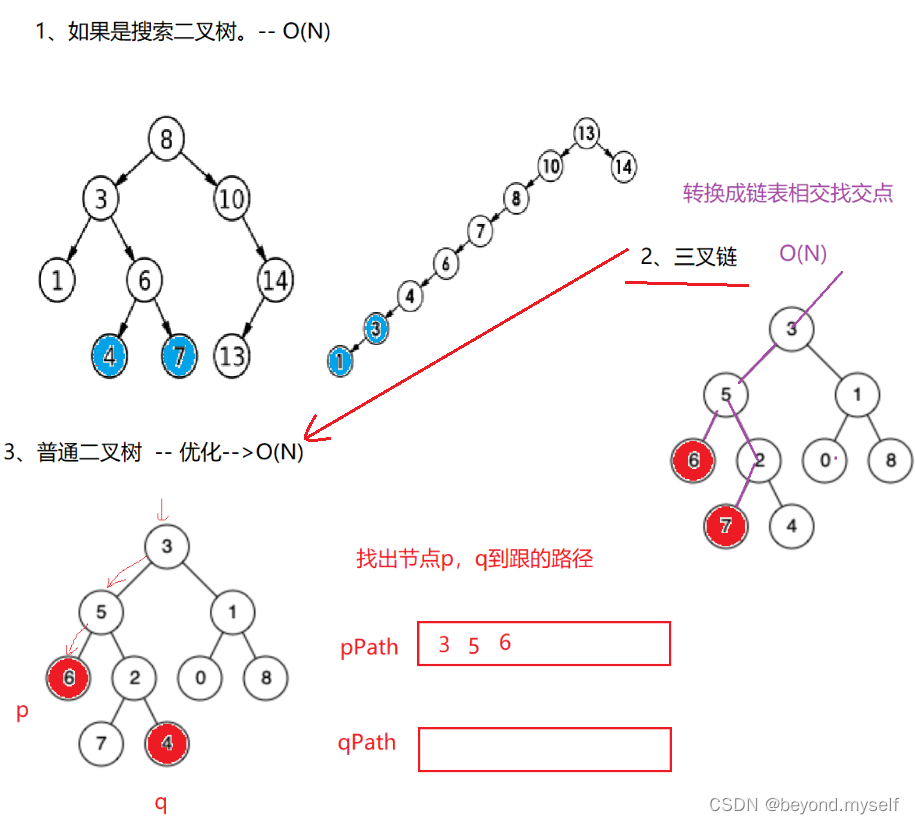
个人手写：
class Solution {
public:
bool FindPath(TreeNode* root,TreeNode* x,stack<TreeNode*>& Path)
{
if(root==nullptr)
return false;
Path.push(root);
if(root==x)
return true;
if(FindPath(root->left,x,Path))
return true;
if(FindPath(root->right,x,Path))
return true;
// root不是要找的节点x，左子树和右子树都没有找到，那么root不是x的的路径中节点，
Path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> pPath,qPath;
FindPath(root,p,pPath);
FindPath(root,q,qPath);
while(pPath.size()<qPath.size())
{
qPath.pop();
}
while(pPath.size()>qPath.size())
{
pPath.pop();
}
while(qPath.top() != pPath.top())
{
qPath.pop();
pPath.pop();
}
return pPath.top();
}
};官方写法：
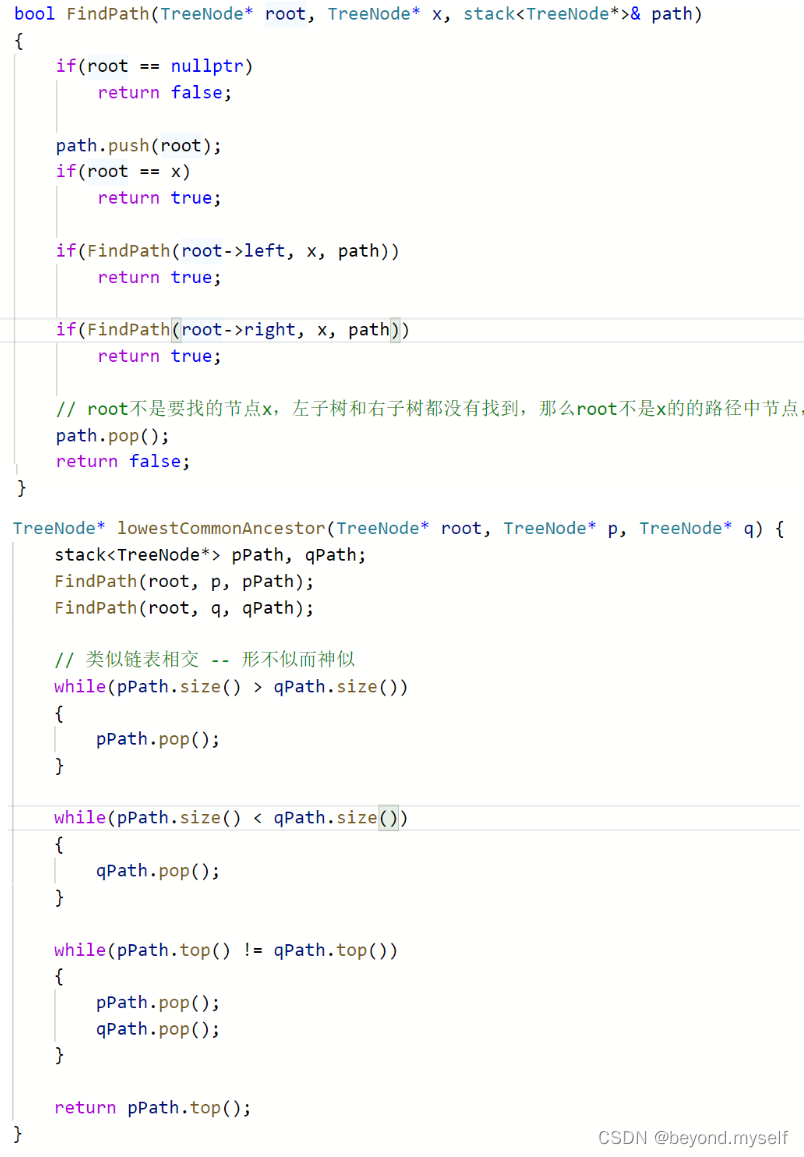
4.二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)?
中序遍历时，把每一个节点的left和right指向改变成head和tail双向链表的形式，用prev记录上一个节点， 让 pRootOfTree 的left指向prev，并让prev的right指向自己，以此类推
个人手写：
class Solution {
public:
void InOrderConvert(TreeNode* pRootOfTree,TreeNode*& prev)
{
if(pRootOfTree==nullptr)
{
return ;
}
InOrderConvert( pRootOfTree->left,prev);
pRootOfTree->left=prev;
if(prev)
{
prev->right= pRootOfTree;
}
prev=pRootOfTree;
InOrderConvert( pRootOfTree->right,prev);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
if(pRootOfTree==nullptr)
return nullptr;
TreeNode* prev=nullptr;
InOrderConvert(pRootOfTree,prev);
while(pRootOfTree->left)
{
pRootOfTree=pRootOfTree->left;
}
return pRootOfTree;
}
};官方写法：?
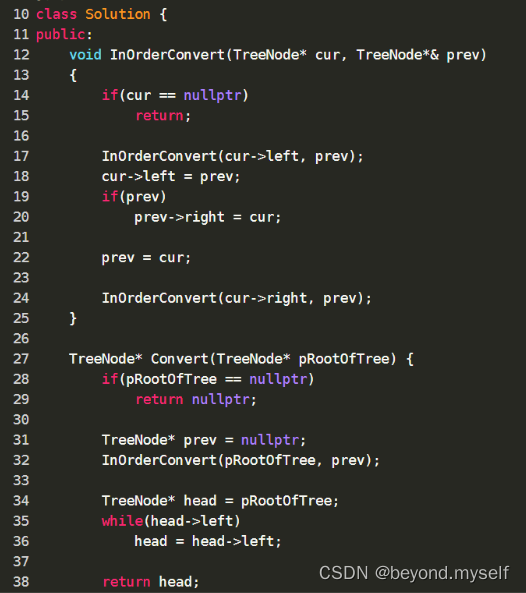
5.105. 从前序与中序遍历序列构造二叉树
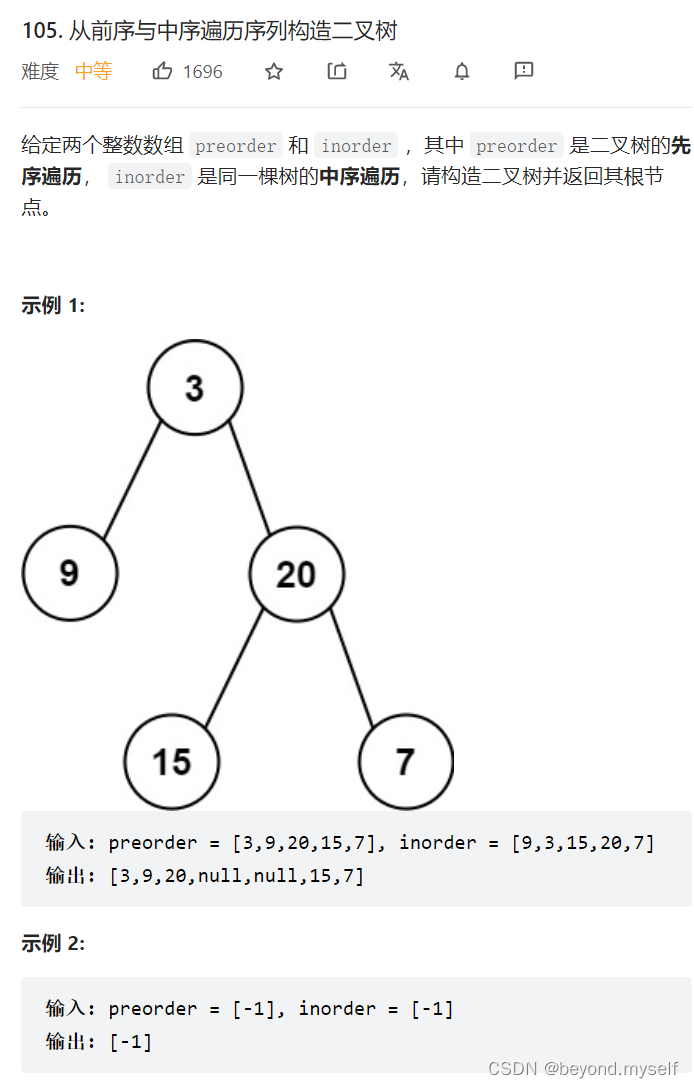
思路：
前序:根、左子树、右子树--依次确定根
中序:左子树、根、右子树--划分左右子树区间
个人手写：
class Solution {
public:
TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,
int& prei,int inbegin,int inend)
{
if(inbegin>inend)
{
return nullptr;
}
TreeNode* root=new TreeNode(preorder[prei]);
int rooti=0;
while(inorder[rooti]!=preorder[prei])
{
++rooti;
}
++prei;
root->left=_buildTree(preorder,inorder,prei,inbegin,rooti-1);
root->right=_buildTree(preorder,inorder,prei,rooti+1,inend);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int prei=0,inbegin=0,inend=inorder.size()-1;
return _buildTree(preorder,inorder,prei,inbegin,inend);
}
};官方写法：
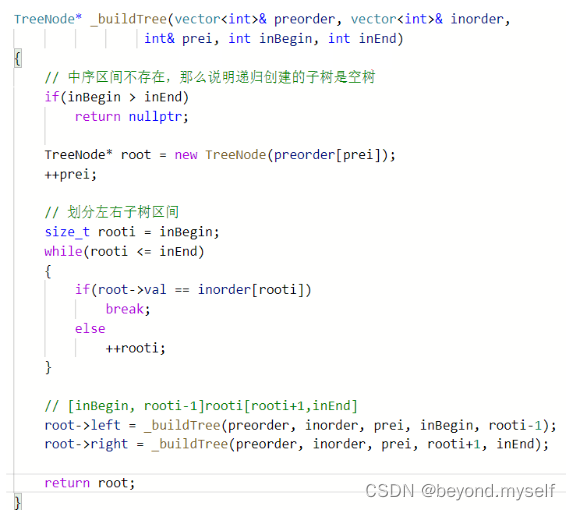
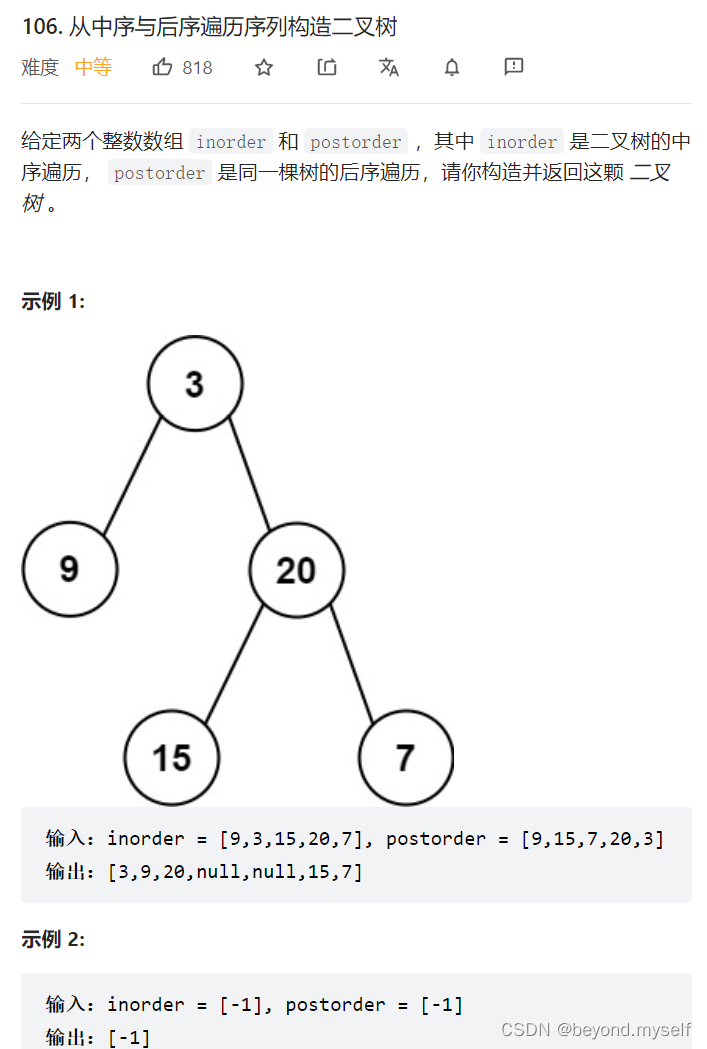
6.?106. 从中序与后序遍历序列构造二叉树
与5类似
class Solution {
public:
TreeNode* _buildTree(vector<int>& postorder, vector<int>& inorder,
int& backi,int inbegin,int inend)
{
if(inbegin>inend)
{
return nullptr;
}
TreeNode* root=new TreeNode(postorder[backi]);
int rooti=0;
while(inorder[rooti]!=postorder[backi])
{
++rooti;
}
--backi;
root->right=_buildTree(postorder,inorder,backi,rooti+1,inend);
root->left=_buildTree(postorder,inorder,backi,inbegin,rooti-1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int backi=postorder.size()-1,inbegin=0,inend=inorder.size()-1;
//cout<<backi;
return _buildTree(postorder,inorder,backi,inbegin,inend);
}
};??_buildTree 子函数注意顺序，当时调试了很久才知道是顺序错了。
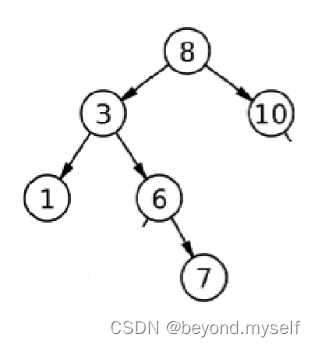
7.自己写不出来的非递归(难)144. 二叉树的前序遍历
看这个树：
?
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> v;
stack<TreeNode*> st;
TreeNode* cur=root;
while(cur||!st.empty())
{
while(cur)
{
v.push_back(cur->val);
st.push(cur);
cur=cur->left;
}
TreeNode* top=st.top();
st.pop();
cur=top->right;
}
return v;
}
};解析：
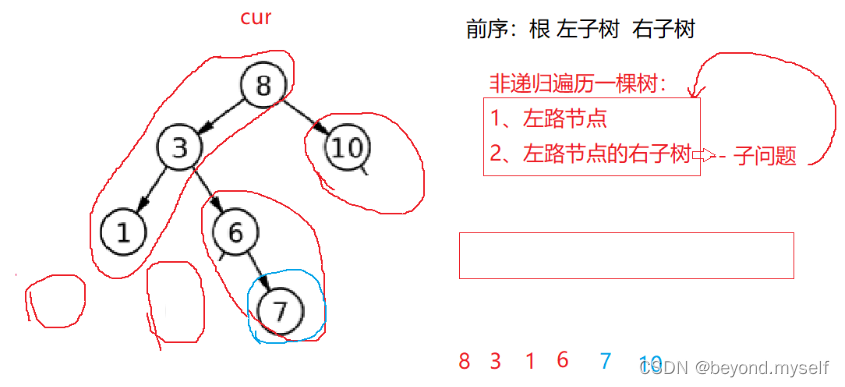
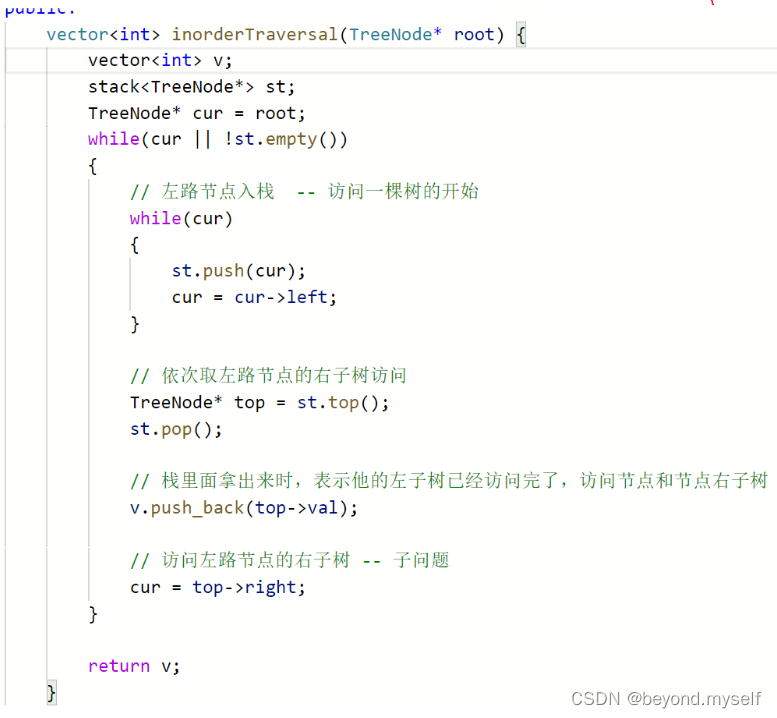
8.同7题类型的中序?94. 二叉树的中序遍历
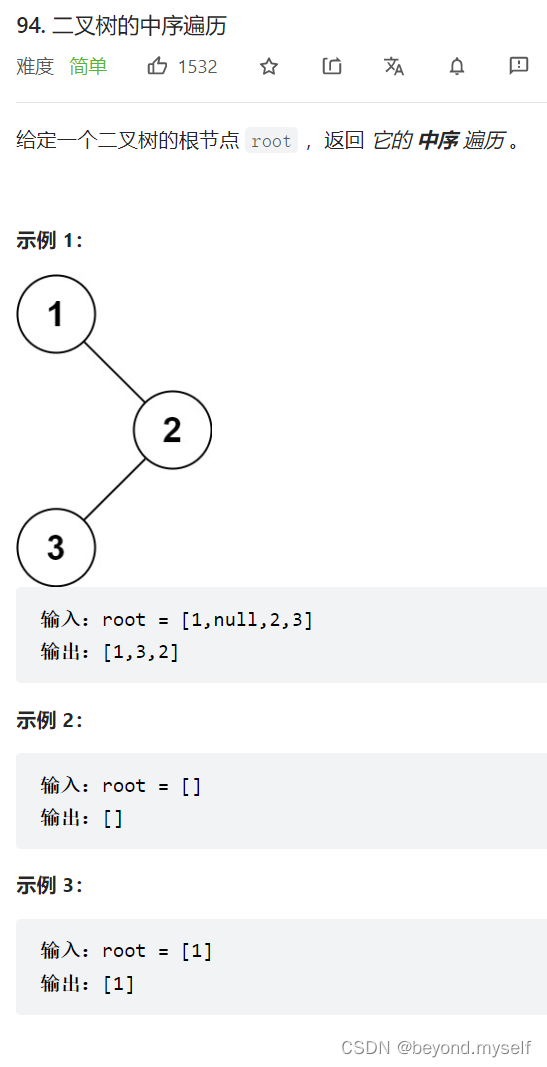
看这个树：
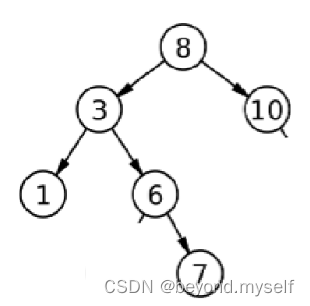先走到1,把1入v，cur= 1的右，1的右为空，再进入循环后，把3入v，然后开始访问3的右
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> v;
stack<TreeNode*> st;
TreeNode* cur=root;
while(cur||!st.empty())
{
while(cur)
{
st.push(cur);
cur=cur->left;
}
TreeNode* top=st.top();
st.pop();
v.push_back(top->val);
cur=top->right;
}
return v;
}
};左路节点入栈一个，一个节点从栈中出来时，他的左子树就算访问完了。访问他及他的右子树。
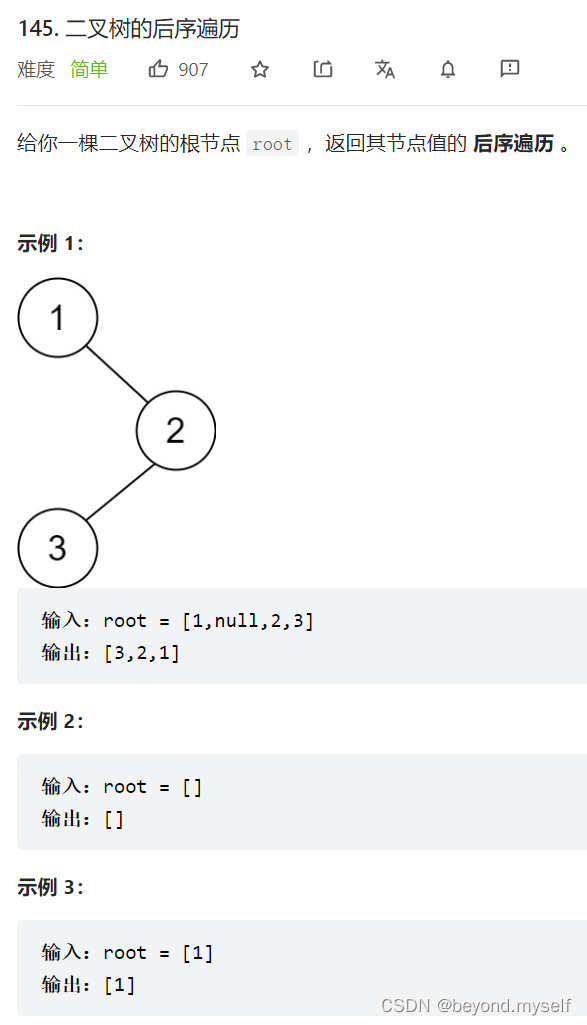
9.145. 二叉树的后序遍历
?
传统递归写法：
class Solution {
public:
void _postorderTraversal(TreeNode* root,vector<int>& v)
{
if(root==nullptr)
return ;
_postorderTraversal(root->left,v);
_postorderTraversal(root->right,v);
v.push_back(root->val);
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int> v;
_postorderTraversal(root,v);
return v;
}
};非递归法（重点）：
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> v;
stack<TreeNode*> st;
TreeNode* cur=root;
TreeNode* prev=nullptr;
while(cur||!st.empty())
{
while(cur)
{
st.push(cur);
cur=cur->left;
}
TreeNode* top=st.top();
// 1.top的左子树已经访问过了，如果top->right==nullptr,说明没有右节点，则可以直接
//访问此节点，把节点插入v中访问过这个节点后，这个节点就成为上一个访问的节点，用
//prev=top;来记录。
// 2.top->right!=nullptr时，如果top->right==prev，即他上一个访问的节点是右节点，右节
//点已访问过，则可以访问这个节点
if(top->right==nullptr||top->right==prev)
{
v.push_back(top->val);
st.pop();
prev=top;
}
else
{
cur=top->right;
}
}
return v;
}
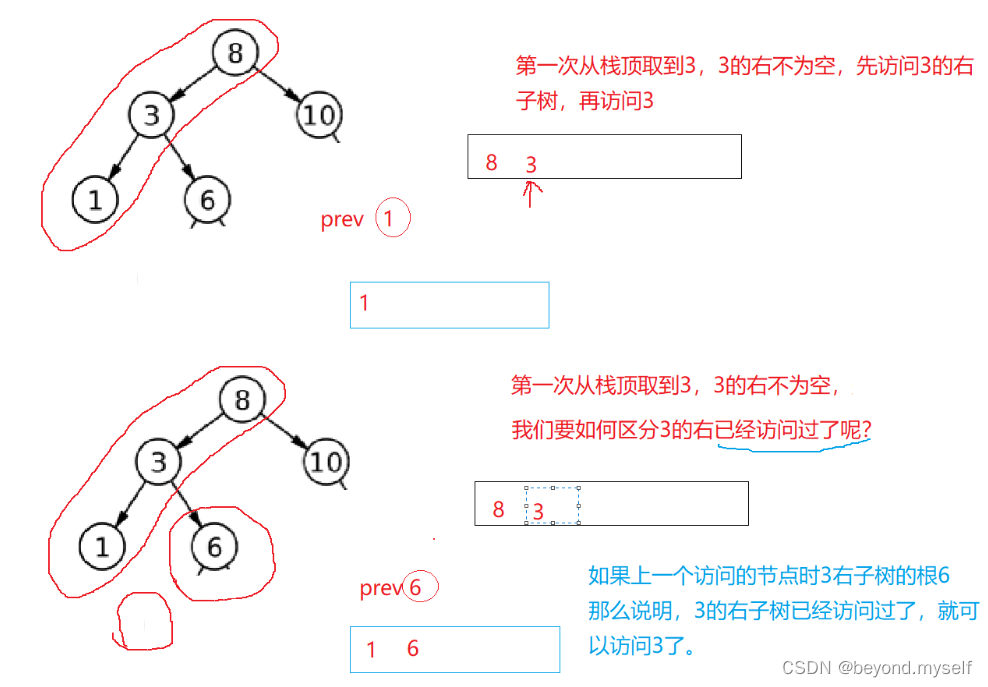
};?解释：
1.while(cur)后 top的左子树已经访问过，如果top->right==nullptr，说明没有右节点，则可以直接访问此节点，把节点插入v中访问过这个节点后，这个节点就成为上一个访问的节点，用prev=top;来记录。
2.top->right!=nullptr时，如果top->right==prev，即他上一个访问的节点是右节点，右节点已访问过，则可以访问这个节点
?