函数的递归与迭代问题
题记——
颠簸于批判主义的无边波浪之中,我们需要寻找一块陆地构建自己的理想。
一、什么是递归?
递(递推)归(回归)
程序调用自身的编程技巧称为递归( recursion)。
递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,
递归策略:
只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量
递归的主要思考方式在于:把大事化小
eg:
main函数自己调用自己的递归
#include<stdio.h>
int main()
{
printf("hehe\n");
main();
return 0;
}
运行结果如图所示:

二、递归的两个必要条件
存在限制条件,当满足这个限制条件的时候,递归便不再继续。
每次递归调用之后越来越接近这个限制条件。
2.1递归练习1
接受一个整型值(无符号),按照顺序打印它的每一位。
例如:
输入:1234,输出 1 2 3 4
# define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void print(unsigned int m)
{
if (m > 9)
{
print(m / 10);
}
printf("%d", m % 10);
}
int main()
{
unsigned int n = 0;
scanf("%u", &n);
print(n);
return 0;
}
}

运行流程演示
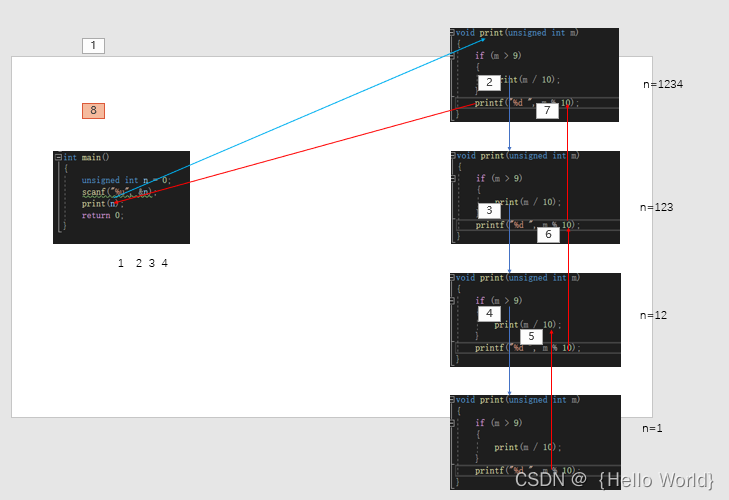
2.2递归练习2
编写函数不允许创建临时变量,求字符串的长度。
首先如果不按照题目的要求,我们可以直接通过strlen求出字符串的长度,例如
#include<stdio.h>
#include<string.h>
int main()
{
char arr[] ="abc" ;
printf("%d", strlen(arr));
return 0;
}

但是题目中要求创建函数且不能创建临时变量,这就引发了我们的思考。
首先我们分析的函数strlen的原理是遇到‘\0’立即停止计数,这由此我们可以作为其解决问题的出发点来编写如下函数:
//递归条件
int my_strlen(char* str)
{
if (*str != '\0')//判断条件
{
return 1 + my_strlen(str + 1);///需要注意
}
else
return 0;
}
#include<stdio.h>
int main()
{
char arr[] = "abc";
int len = my_strlen(arr);//调用函数
printf("%d\n",len);
return 0;
}

三、什么是迭代
迭代是重复反馈过程的活动,其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”,而每一次迭代得到的结果会作为下一次迭代的初始值。
重复执行一系列运算步骤,从前面的量依次求出后面的量的过程。此过程的每一次结果,都是由对前一次所得结果施行相同的运算步骤得到的。例如利用迭代法求某一数学问题的解。
对计算机特定程序中需要反复执行的子程序(一组指令),进行一次重复,即重复执行程序中的循环,直到满足某条件为止,亦称为迭代。
四、递归与迭代
4.1求n的阶乘。(不考虑溢出)
通过数学知识,我们可以知道n!=n*(n-1)!,那么我们便可以极其轻松的解决此问题,首先介绍递归的方法如下
//求n的阶乘
#include<stdio.h>
int function_1(int n)
{
if (n <= 1)
{
return 1;
}
else
return n * function_1(n - 1);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = function_1(n);
printf("%d", ret);
return 0;
}
运行结果:

迭代方法:
#include<stdio.h>
int function_2(int n)
{
int i = 0;
int ret = 1;
for (i = 1; i <= n; i++)
{
ret = ret * i;
}
return ret;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = function_2(n);
printf("%d", ret);
return 0;
}
运行结果:

4.2求第n个斐波那契数。(不考虑溢出)
4.2.1 斐波那契数列的介绍
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N)*
4.2.2解决方法
该问题有两种解决方案,第一种运用公式**F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N)***解决
代码如下:
#include<stdio.h>
int fib(int n)
{
if (n <= 2)
{
return 1;
}
else
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d", ret);
return 0;
}
运行结果如下:
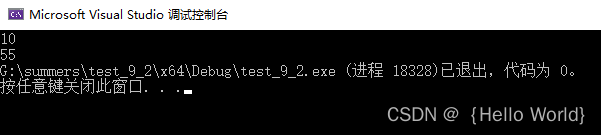
但是当我们去求50的斐波那契数时,可以发现如下结果:

所以我们可以发现求斐波那契数采用递归的方法是并不合适的。
第二种方案运用非递归的方法:前两个斐波那契数相加等于第三个斐波那契数
#include<stdio.h>
int fib(n)
{
int a = 1;
int b = 1;
int c = 1;
while (n > 2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d", ret);
return 0;
}
