[C++知识库]写一个math.c

学习目标：

用c语言编写math中各种函数

• 绝对值
• 幂运算(整数)
• 开方运算(整数)
• 幂运算(有理数)
• 对数
• 倒数
• 阶乘
• 排列
• 组合
• 三角函数
  • 正弦函数
  • 余弦函数
  • 正切函数

绝对值

• 目标
  给一个参数，返回它的绝对值。
• 代码

double Absolute_Value(double Number){
	return Number>0?Number:-Number;
} 

• 解
  • 当调用absolute_Value函数时，创建double 类型的变量Number
  • 将输入的参数值赋给Number
  • 判断Number是否大于0，是返回Number，不是返回-Number

幂运算(整数)

• 目标
  给一个底数Number，一个指数Secondary，返回Number的Secondary次方。
• 代码

double Power(double Number,int Secondary){
	double PowerNumber = 1;
	if(Secondary < 0){
		Secondary = -Secondary;
		Number = 1/Number;
	}
	while(Secondary--){
		PowerNumber*=Number;
	}
	return PowerNumber;
} 

• 解
  • if判断，将指数变成正整数，若指数是负数，将底数取它的倒数
  • while循环，指数是多少，1就乘几次底数

后面因为要多次用到幂运算，这里再把代码修改一下
一个函数将指数变成正整数，另一个执行幂运算

//{Number>=0|Number∈R} {Secondary>0|Secondary∈N+}
double Power_Start(double Number,int Secondary){
	double PowerNumber = 1;
	while(Secondary--){
		PowerNumber*=Number;
	}
	return 
}
double Power(double Number,int Secondary){
	if(Secondary < 0){
		Secondary = -Secondary;
		Number = 1/Number;
	}
	return Power_Start(Number,Secondary);
} 

开方运算(整数)

• 目标
  给一个被开方数Number，一个开方次数Secondary，返回Number开Secondary次的根。

方法一：二分法

??取1到被开方数Number的一半值a作偏移值，设x₀等于被开方数，看根在x_n的哪边，就往哪边偏移，每次偏移后，偏移值取自己的一半，使x_n不断接近根。

因为Number>1和Number<1的情况不太一样，所以当输入不同的值时，运算的方法可能不一样，这里举个实际的例子，看看是要怎么处理。

求8开3次的根x

假设x₀=8，因为x₀>1，设偏移值a₀=(8-1)÷2=3.5,
x₀现在肯定是大于根x，所以x₁=x₀-a₀=8-3.5=4.5
a₁=a₀÷2
d₁=x₁³-8

如果d₁>0,说明x₁>x,所以x₂=x₁-a₁
a₂=a₁÷2
d₂=x₂³-8
如果d₁<0,说明x₁<x,所以x₂=x₁+a₁
a₂=a₁÷2
d₂=x₂³-8

同理判断，直到d_n<0.000001

求0.125开3次的根x

假设x₀=0.125，因为x₀<1，设偏移值a₀=(1-0.125)÷2
x₀现在肯定是小于根x，所以x₁=x₀+a₀
a₁=a₀÷2
d₁=x₁³-0.125

如果d₁>0,说明x₁>x,所以x₂=x₁-a₁
a₂=a₁÷2
d₂=x₂³-8
如果d₁<0,说明x₁<x,所以x₂=x₁+a₁
a₂=a₁÷2
d₂=x₂³-8

同理判断，直到d_n<0.000001

由上可以知道开最开始的处理会有不一样，在求近似根时是一样的。

因为开方次数Secondary和被开方数Number都有可能是负数，所以在求根之前要先把得到的数都变成正数。

如果Number<0,Secondary是2的倍数，实数内无解
如果Number<0,Secondary不是2的倍数，Number=-Number，作一个标记flag
如果Number ==0,根x ==0
如果Secondary<0,Number取其倒数，Secondary取绝对值
如果Secondary ==0,无法开根>

• 代码

//开方准备
char Prescrption_Ready(double *Number,int Secondary,char *flag){
	if(Number<=0){
		if((int)Absolute_Value(*Secondary)%2==0){
			return 0xff;
		}else if(Number == 0){
			return 0;
		}else{
			*Number=-*Number;
			*flag=1;
		}
	}

	if(Secondary<=0){
		if(Secondary == 0){
			return 0xff;
		}else{
			*Number=1/(*Number);
			*Secondary=-*Secondary;
		}
	}

	return 1;
}

/*开方
MightRoot:		可能根
OffsetValue：	偏移值
DifferenceValue:偏差值
flag:         	标记符号
*/
double Prescrption(double Number,int Secondary){
	double MightRoot,OffsetValue,DifferenceValue;
	char flag=0;

	//将参数变成正数
	if(Prescrption_Ready(&Number,&Secondary,&flag)!=1){
		return Prescrption_Ready(&Number,&Secondary,&flag);
	}

	//为开方作第一次准备
	MightRoot=Number;
    OffsetValue=Absolute_Value(MightRoot - 1)/2; 
    DifferenceValue = Number>1?1:-1;
    
	do{
		//偏移
        if(DifferenceValue>0){
                MightRoot-=OffsetValue;
        }else{
                MightRoot+=OffsetValue;
        }

		//下一次的偏移值
        OffsetValue/=2;

		//这次的偏差值
        if(Number>1){
            DifferenceValue = Power_Start(MightRoot,Secondary) - Number;
        }else{
            DifferenceValue = 1/Number - 1/Power_Start(MightRoot,Secondary);
        }
    }while(Absolute_Value(DifferenceValue) > 0.00001);			//0.00001是允许的最小误差
    
    if(flag){
        return -MightRoot;
    }else{
        return MightRoot;
    }
} 

其中当Number<1时，计算误差值计算两个幂的倒数差，可以增大精度，但这样会增加每次循环的负担，所以又加了一个倒数标记，在开方准备时，把被开方数变成大于1的数；

/*开方准备
Number_R     --->  Number_R     >0
Secondary_R  --->  Secondary_R  >0    &&    Nflag_R记符号   Fflag_R记是否是倒数
*/
char Prescrption_Ready(double* Number_R,int* Secondary_R,char* Nflag_R,char* Fflag_R){
    if(*Number_R<=0){
        if((int)Absolute_Value(*Secondary_R)%2==0){
            return 0xff;
        }else if(*Number_R==0){
            return 0;
        }else{
            *Number_R=-*Number_R;
            *Nflag_R=1;
        }
    }

    if(*Secondary_R<=0){
        if(*Secondary_R==0){
            return 0xff;
        }else{
            *Number_R = 1/(*Number_R);
            *Secondary_R = -*Secondary_R;
        }
    }

    if(*Number_R < 1){
        *Number_R = 1/(*Number_R);
        *Fflag_R = 1;
    }

    return 1;
}

/*开方*方法一
MightRoot:		可能根
OffsetValue：	偏移值
DifferenceValue:偏差值
NegativeFlag:   标记符号
FallFlag:       标记倒数
*/
double Prescrption1(double Number,int Secondary){
	double MightRoot,OffsetValue,DifferenceValue;
	char NegativeFlag=0,FallFlag=0;

	//将参数变成正数
	if(Prescrption_Ready(&Number,&Secondary,&NegativeFlag,&FallFlag)!=1){
		return Prescrption_Ready(&Number,&Secondary,&NegativeFlag,&FallFlag);
	}

	//为开方作第一次准备
	MightRoot=Number;
    OffsetValue=Absolute_Value(MightRoot - 1)/2; 
    DifferenceValue = Number>1?1:-1;
    
	do{
		//偏移
        if(DifferenceValue>0){
                MightRoot-=OffsetValue;
        }else{
                MightRoot+=OffsetValue;
        }

		//下一次的偏移值
        OffsetValue/=2;

		//这次的偏差值
        DifferenceValue = Power_Start(MightRoot,Secondary) - Number;
    }while(Absolute_Value(DifferenceValue) > 0.00001);			//0.00001是允许的最小误差

    if(NegativeFlag){
        MightRoot = -MightRoot;
    }
    if(FallFlag){
        return 1/MightRoot;
    }else{
        return MightRoot;
    }
}

方法二：牛顿迭代法

??在方法一实现后想知道有没有更加快的求根方法，在网上看到叫“牛顿迭代法”的方式求根，所以也试着去实现。

设r是f(x)的根，选取x₀作为r的初始近似值，过点(x₀,f(x₀))做曲线 的切线L₀，L₀：y=f(x₀)+f’(x₀) (x-x₀)，则L₀与x轴交点的横坐标x₁=x₀-f(x₀)/f’(x₀) ，称x₁为r的一次近似值。过点(x₁,f(x₁))做曲线y=f(x)的切线，并求该切线与x轴交点的横坐标x₂=x₁-f(x₁)/f’(x₁) ，称x₂为r的二次近似值。重复以上过程，得r的近似值序列，其中，x_n+1=x_n-f(x_n)/f’(x_n)称为r的n+1次近似值，上式称为牛顿迭代公式。
牛顿迭代法

??根据牛顿迭代法的解释，求一下开方的求根公式。

求开方的值，就是在就求幂的底数，如8的3次开方，就是求几的3次方等于8，换成公式：
求y=³√x的y，就是求y=x³的x，举一个实际例子

---

已知被开数Number=27和开方次数Secondary=3，求根
即在y=xⁿ中已知y=27，n=3，求x

8=x³
0=x³-27
设y=x³-27
设x₀=27，过(x₀，x₀³-27)作y的切线l₁:y=k₁x+b₁
∵y’=3x²
∴k₁=3x₀²
∵l₁过点(x₀,x₀³-27)
∴x₀³-27=k₁x₀+b₁
?x₀³-27=3x₀²x₀+b~1
?x₀³-27=3x₀³+b₁
?b₁=-2x₀³-27
∴l₁:y=3x₀²x-2x₀³-27
l₁交x轴时，y=0，0=3x₀²x-2x₀³-27，得x₁=(2x₀³+27)/3x₀²
同上：x_i=(2x_i-1³+27)/3x_i-1²

通过上面的过程可以得到一个就近视根的公式，把旧的值代入公式得到的新的值会更加接近根，现在> 求一下开方求解的通用接近公式。

y=xⁿ,当y=a时，求x
a=xⁿ
0=xⁿ-a
设y=xⁿ-a
设x₀=a，过(x₀，x₀ⁿ-a)作y的切线l₁:y=k₁x+b₁
∵y’=nx^n-1
∴k₁=nx₀^n-1
∵l₁过点(x₀,x₀ⁿ-a)
∴x₀ⁿ-a=k₁x₀+b₁
?x₀ⁿ-a=nx₀ⁿ+b₁
?b₁=(1-n)x₀ⁿ-a
∴l₁:y=nx₀^n-1x+(1-n)x₀ⁿ-a
l₁交x轴时，y=0，0=nx₀^n-1x+(1-n)x₀ⁿ - a，得x₁=((n-1)x₀ⁿ+a)/(nx₀^n-1)
同上：x_i=((n - 1)x_i-1ⁿ+a)/(nx_i-1^n-1)
化简：x_i=a/(nx_i-1^n-1) + x_i-1 - x_i/n

由上可知，函数里需要有变量近视值，近似值的开方次数-1的幂，还有误差值

• 代码

/*开方准备
Number_R     --->  Number_R     >0
Secondary_R  --->  Secondary_R  >0    &&    Nflag_R记符号   Fflag_R记是否是倒数
*/
char Prescrption_Ready(double* Number_R,int* Secondary_R,char* Nflag_R,char* Fflag_R){
    if(*Number_R<=0){
        if((int)Absolute_Value(*Secondary_R)%2==0){
            return 0xff;
        }else if(*Number_R==0){
            return 0;
        }else{
            *Number_R=-*Number_R;
            *Nflag_R=1;
        }
    }

    if(*Secondary_R<=0){
        if(*Secondary_R==0){
            return 0xff;
        }else{
            *Number_R = 1/(*Number_R);
            *Secondary_R = -*Secondary_R;
        }
    }

    if(*Number_R < 1){
        *Number_R = 1/(*Number_R);
        *Fflag_R = 1;
    }

    return 1;
}

/*开方*方法二
MightRoot:		可能根
Root_Power_1：	可能根的开方次数-1的幂
DifferenceValue:偏差值
flag:         	标记符号
*/
double Prescrption2(double Number,int Secondary){
    double MightRoot,Root_Power_1,DifferenceValue;
    char NegativeFlag=0,FallFlag=0;

	//将参数变成正数
    if(Prescrption_Ready(&Number,&Secondary,&NegativeFlag,&FallFlag)!=1){
		return Prescrption_Ready(&Number,&Secondary,&NegativeFlag,&FallFlag);
	}

	//为开方作第一次准备
    MightRoot=Number;
    Root_Power_1 = Power_Start(MightRoot,Secondary-1);

    do{
    	//通过牛顿迭代法得到的公式求近视根
        MightRoot = Number/(Secondary*Root_Power_1)+MightRoot-MightRoot/Secondary;

		//近视根的开方次数-1的次方
        Root_Power_1 = Power_Start(MightRoot,Secondary-1);

		//这次的偏差值
        DifferenceValue = Root_Power_1*MightRoot - Number;
    }while(Absolute_Value(DifferenceValue) > 0.00001);         //0.00001是允许的最小误差

    if(NegativeFlag){
        MightRoot = -MightRoot;
    }
    if(FallFlag){
        return 1/MightRoot;
    }else{
        return MightRoot;
    }
} 

使用stm32时钟计时，发现当开方次数<3时，牛顿迭代法十分的快，当开方次数>3时，方法一反而会快一些，如果开方次数更大，方法二的速度会比方法一快得多，所以又写了一个函数，来切换使用方法一和方法二。

double Prescrption(double *Number,int *Secondary){
	if(Absolute_Value(*Secondary) > 3 ){
		if(260-Absolute_Value(*Secondary)*40.0<Absolute_Value(*Number)){
			return Prescrption1(*Number,*Secondary);
		}
	}
	return Prescrption2(*Number,*Secondary);
}

_{方法二比方法一慢是因为当次数过大时，使用切线不能快速接近根，要执行几百几千次才可以。
更快的求解可以在第一次MightRoot入手，目前我把它改成了MightRoot=1+(Number-1)/Power_Start(3.0,Secondary-1);}

方法三：神秘常数

??有一段时间没有写，在网上看到一个新的得到开二次方后倒数的方法，他的原理不是很明白，这里就附上他的代码：

float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;
	
	x2 = number * 0.5F;
	y  = number;
	i  = * ( long * ) &y;
	i  = 0x5f3759df - ( i >> 1 );
	y  = * ( float * ) &i;
	y  = y * ( threehalfs - ( x2 * y * y ) ); //这里类似牛顿迭代法可以多次计算，提高精度
	y  = y * ( threehalfs - ( x2 * y * y ) ); 

	return y;
}

幂运算(有理数)

• 目标
  给一个底数Number，一个指数Secondary，返回Number的Secondary次方。

方法一：十进制

??这可能是最笨的办法了吧，但也是最简单的。
??先提出次数的整数部分，进行整数幂运算，次数减去整数，之后把次数乘10，底数开十次根，再次提出次数的整数部分，进行整数幂运算，次数减去整数，这样不断循环，直到次数等于0或者底数被开到足够小。
??这里举个例子：

求8的2.25次幂

---

设M_n为解，S_n为剩余次数，E_n为被开第n次的底数
M₁=8²=64
S₁=2.25-2=0.25

E₁=8^1/10=1.2311444133
S₁=0.25*10=2.5
M₂=M₁*E₁²
S₂=S₁-2=0.5

这是第一次循环

E₂=E₁^1/10
S₂=0.5*10=5.0
M₃=M₂*E₂⁵
S₃=S₂-5=0

因为S₃=0，最后解就是S₃

这个方法每次都要把底数开10次，当底数是负数时不能开根，所以不能解底数是负数的运算。

• 代码

/*幂运算(有理数)
方法一：十进制

Number          底数
Secondary       次数/剩余的次数

mightRoot       可能解
mightRootAddEnd 开n次后的底数
Secondarying    次数的整数部分
FallFlag:       标记倒数
*/
double Power_(double Number,double Secondary){
    double mightRoot=1,mightRootAddEnd=Number;
    unsigned int Secondarying;
    unsigned char FallFlag=0;

    //判断底数是否是非正数
    if(Number<=0){
        return 0;
    }

    //判断次数是否是零
    if(Secondary==0){
        return 1;
    }

    //判断次数是否是负数
    if(Secondary<0){
        mightRoot=1/mightRoot;
        Secondary=-Secondary;
        FallFlag=1;
    }

    while(1){
        //得到次数的整数部分
        Secondarying=Secondary;

        //得到可能根
        mightRoot*=Power_Start(mightRootAddEnd,Secondarying);

        //次数是否运算结束或者底数被开得是否足够小
        Secondary-=Secondarying;
        if(Secondary==0 || mightRootAddEnd<1.000001){
            break;
        }

        //为下一次运算作准备
        Secondary*=10;
        mightRootAddEnd=Prescrption(mightRootAddEnd,10);//底数开10次
    }

    if(FallFlag){
        return 1/mightRoot;
    }
    else{
        return mightRoot;
    }
}

对数

• 目标
  给一个底数BottomNum，一个真数NationsNum：，返回以BottomNum为底NationsNum的对数。

方法一：十进制

??向幂运算(有理数)时一样，先求出整数部分，求小数部分时，将底数开十次，求十分位上的值，再将底数开十次，求千分位上的值，这样循环，直到解在允许误差内。举个例子。

求log₁₀₂₄4194304。(1024^2.2=4194304)

---

设M_n为解，B_n为底数，A_n为当前求的位数，E_n为当前求的位数上的值，N为1024的M_n次
M₀=0
A₁=1
E₁=0
B₁=1024
N=1

N=N* B₁=1 * 1024=1024
N<4194304
E₁=E₁+1=0+1=1
N=N+B₁=1024 * 1024=1048576
N<4194304
E₁=E₁+1=1+1=2
N=N+B₁=1048576*1024=1073741824
N>4194304

N=1048576
M₁=M₀+A₁* E₁=0+1*2=2
A₂=A₂/10=1/10=0.1
E₂=0
B₂=B₁^1/10=1024^1/10=2
4194304-N>0.00001

N=NB₂=1048576 * 2=2097152
N<4194304
E₂=E₂+1=0+1=1
N=NB₂=2097152* 2=4194304
N == 4194304
E₂=E₂+1=1+1=2
N=N*B₂=4194304 * 2=8388608
N>4194304

N=4194304
M₂=M₀+A₁* E₁=2+0.1*2=2.2
A₃=A₂/10=0.1/10=0.01
E₃=0
B₃=B₁^1/10=2^1/10
4194304-N<0.00001

---

解等于M₂=2.2

• 代码
  因为每次底数要开十次，底数不能为负数。

/*对数
BottomNum:      底数
NationsNum：    真数

BottomNumAdd:   对应小数位数
NumAddEnd:      对应小数位上的值
UnNationsNum：  解的真数
Untion:         解

NegativeFlag:   标记符号
*/
double logarithm(double BottomNum,double NationsNum){
    double Untion=0,UnNationsNum,NumAddEnd;
    unsigned char BottomNumAdd=0;
    char NegativeFlag=0;

    //判断参数是否是正数
    if(NationsNum<=0 || BottomNum<=0){
        return 0;
    }

    //将底数变成大于1的数
    if(BottomNum<1){
        BottomNum=1/BottomNum;
        NegativeFlag=!NegativeFlag;
    }

    //将真数变成大于1的数
    if(NationsNum<0){
        NationsNum=1/NationsNum;
        NegativeFlag=!NegativeFlag;
    }

    //开始求解准备
    UnNationsNum=1;             //求解时的作比较值
    NumAddEnd=1;                //指向解的第几位，从个位开始1-->0.1-->0.01
    BottomNumAdd=0;             //解的第几位的值

    do{
        //计算当前位数上的值
        while(UnNationsNum*BottomNum<=NationsNum){
            UnNationsNum*=BottomNum;
            BottomNumAdd+=1;
        }

        //将计算出的值加到解上
        Untion+=BottomNumAdd*NumAddEnd;

        //为求下一位作准备
        BottomNumAdd=0;
        NumAddEnd/=10;
        BottomNum=Prescrption(BottomNum,10);

    //判断误差是否在允许范围内
    }while(NationsNum-UnNationsNum>0.000001);

    if(NegativeFlag){
        return -Untion;
    }
    else{
        return Untion;
    }
}

倒数

• 目标
  给一个数Number，返回Numberd的倒数。
• 代码

double Reciprecal(double Number){
	if(Number==0){
		return 0;
	}
	else{
		return 1.0 / Number;
	}
} 

• 解
  • 当调用Reciprecal函数时，创建double 类型的变量Number
  • 将输入的参数值赋给Number
  • 判断Number是否为0，是返回0，不是返回1/Number

阶乘

• 目标
  给一个数Number，返回Numberd的阶乘。
• 代码

unsigned long Factorial(unsigned short Number){
	unsigned long Value=1;
	while(Number){
        Value*=Number--;
    }
    return Value;
} 

• 解
  • 当调用Factorial函数时，创建unsigned short类型的变量Number
  • 将输入的参数值赋给Number
  • 循环判断Number是否为0，是返回Value，不是Value再乘上Number，Number-1

排列

• 目标
  给一个总数Total，取出个数Number，返回有多少种排列方法。
• 代码

unsigned int Arrangement(unsigned short Total ,unsigned short Number) {
    if(Number > Total){
        return 0xFFFFFFFF;
    }
    return Factorial(Total)/Factorial(Total-Number);
}

• 解
  • 当调用Factorial函数时，创建两个unsigned short类型的变量Total和Number
  • 将输入的参数值赋给Total和Number
  • 判断取出个数Number是否大于总个数Total，是退出函数并返回0xFFFFFFFF
  • 计算Total的阶乘和(Total-Number)的阶乘，返回它们的商

组合

• 目标
  给一个总数Total，取出个数Number，返回有多少种组合方法。
• 代码

unsigned int Combination(unsigned short Total ,unsigned short Number){
    if(Number > Total){
        return 0xFFFFFFFF;
    }
    return Arrangement(Total,Number)*Factorial(Number);
} 

• 解
  • 当调用Factorial函数时，创建两个unsigned short类型的变量Total和Number
  • 将输入的参数值赋给Total和Number
  • 判断取出个数Number是否大于总个数Total，是退出函数并返回0xFFFFFFFF
  • 计算Total和Number的排列数，排列数再除以Number的阶乘，返回结果

三角函数

??三角函数比较常见的有正弦函数，余弦函数，正切函数，除了这些还有余切函数，正割函数，余割函数。三角函数之间都有关系，只要能求出一个就能求出其他的。

正弦函数

• 目标
  给一个弧度Number，返回sin(Numberd)的值。
• 方法：泰勒展开
  利用微积分的性质，sinx的值等于sin’x与x轴在[0,x]区间组成的面积，根据这个性质可以理解柯西中值定理。

y=sinx
y=sin0+(x-0)sin’x
y=sin0+(x-0)[sin0+(x-0)sin’‘x]
?=sin0+xsin’0+(x-0)²sin’‘x
y=sin0+xsin’0+(x-0)² [sin0+(x-0)sin’‘‘x]
?=sin0+xsin’0+x²sin’‘0+(x-0)³sin’’‘x
y=sin0+xsin’0+x²sin’‘0+(x-0)³ [sin0+(x-0)sin’‘’‘x]
?=sin0+xsin’0+x²sin’‘0+x³sin’‘‘0+(x-0)⁴sin’’‘‘x
… …
y=sin0+xsin’0+x²sin’‘0+x³sin’’‘0+x⁴sin’‘’'0+…
?=sin0+xcos0-x²sin0-x³cos0+x⁴sin0+…
?=0+x*1-x²*0-x³*1+x⁴*0+…
?=x¹-x³+x⁵-x⁷+x⁹-x¹¹+…

但这样求出来的解果离真正的结果误差比较大，由其是(x-x₀)这个值比较大时，在柯西中值定理的基础上改善，推出泰勒展开式。

y=sinx
y=sin0+(x-0)sin’x/1
y=sin0+(x-0)[sin0+(x-0)sin’‘x/2]/1
?=sin0+xsin’0/1+(x-0)²sin’‘x/2/1
?=sin0+xsin’0/1!+(x-0)²sin’‘x/2!
y=sin0+xsin’0/1!+(x-0)² [sin0+(x-0)sin’‘‘x/3]/2!
?=sin0+xsin’0/1!+x²sin’‘0/2!+(x-0)³sin’’‘x/3/2!
?=sin0+xsin’0/1!+x²sin’‘0/2!+(x-0)³sin’‘‘x/3!
y=sin0+xsin’0/1!+x²sin’‘0/2!+(x-0)³ [sin0+(x-0)sin’’‘‘x/4]/3!
?=sin0+xsin’0/1!+x²sin’‘0/2!+x³sin’’‘0/3!+(x-0)⁴sin’‘’‘x/4/3!
?=sin0+xsin’0/1!+x²sin’‘0/2!+x³sin’‘‘0/3!+(x-0)⁴sin’’‘‘x/4!
… …
y=sin0+xsin’0/1!+x²sin’‘0/2!+x³sin’’‘0/3!+x⁴sin’‘’'0/4!+…
?=sin0+xcos0/1!-x²sin0/2!-x³cos0/3!+x⁴sin0/4!+…
?=0+x*1/1!-x²*0/2!-x³*1/3!+x⁴*0/4!+…
?=x¹/1!-x³/3!+x⁵/5!-x⁷/7!+x⁹/9!-x¹¹/11!+…

由上可知sinx的泰勒展开式就是x¹/1!-x³/3!+x⁵/5!-x⁷/7!+x⁹/9!-x¹¹/11!+…

• 代码

#define pi                      3.1415926535897932384626433832795028841971f
/*正弦函数(弧度)
方法一：泰勒级数求值

Radian:      弧度（弧度=π*角度/180）  0~π/2
taylorLever: 泰勒级数
tayloritem:  泰勒项
untie:       解
*/
double Sine_Radian(double Radian){
    double untie=0,taylorStore;
    unsigned short  taylorLever;

    //初始化
    taylorStore = Radian;
    taylorLever = 1;
    Radian *= Radian*-1; //泰勒项每项间的比值

    while(taylorLever<200){
        untie += taylorStore;

        //为下次作准备
        taylorStore*=Radian;
        taylorStore/=(++taylorLever);
        taylorStore/=(++taylorLever);
    }

    return untie;
}

??弧度平时不怎么使用，都是直接使用角度表示，所以又写了一个函数

/*正弦函数(角度)
方法一：泰勒级数
angle:      角度（弧度=π*角度/180）
*/
double Sine_Angle(double angle){
    return Sine_Radian(pi*angle/180);
}

余弦函数

• 目标
  给一个弧度Number，返回sin(Numberd)的值。

方法一：泰勒展开

和正弦函数一样，先求cosx的泰勒展开式。

y=cosx
y=cos0+(x-0)cos’x/1
?=cos0+xcos’x/1
y=cos0+x[cos0+(x-0)cos’‘x/2]/1
?=cos0+xcos’0/1+x²cos’‘x/2/1
?=cos0+xcos’0/1!+x²cos’‘x/2!
y=cos0+xcos’0/1!+x² [cos0+(x-0)cos’‘‘x/3]/2!
?=cos0+xcos’0/1!+x²cos0/2!+x³cos’’‘x/3!
y=cos0+xcos’0/1!+x²cos0/2!+x³ [cos0+(x-0)cos’‘‘x/4]/3!
?=cos0+xcos’0/1!+x²cos0/2!+x³cos’’‘0/3!+x⁴cos’‘’‘x/4!
… …
y=cos0+xcos’0/1!+x²cos0/2!+x³cos’‘‘0/3!+x⁴cos’’''0/4!+…
?=cos0-x¹sin0/1!-x²cos0/2!+x³sin0/3!+x⁴cos0/4!-x⁵sin0/5!-…
?=1-x²/2!+x⁴/4!-x⁶/6!+x⁸/8!-x¹⁰/10!+…

由上可知cosx的泰勒展开式就是1-x²/2!+x⁴/4!-x⁶/6!+x⁸/8!-x¹⁰/10!+…

• 代码

#define pi                      3.1415926535897932384626433832795028841971f
/*余弦函数(弧度)
方法一：泰勒展开求解

Radian:      弧度（弧度=π*角度/180）  0~π/2
taylorLever: 泰勒级数
tayloritem:  泰勒项
untie:       解
*/
double Cosine_Radian(double Radian){
    double untie=0,taylorStore;
    unsigned short  taylorLever;

    //初始化
    taylorStore = 1;
    taylorLever = 1;
    Radian *= Radian*-1; //泰勒项每项间的比值

    while(taylorLever<200){
        untie += taylorStore;

        //为下次作准备
        taylorStore*=Radian;
        taylorStore/=(taylorLever++);
        taylorStore/=(taylorLever++);
    }

    return untie;
}

方法二：调用正弦函数

因为cos(90-x)=sinx所以可以直接用之前写好的正弦求解

• 代码

#define pi                      3.1415926535897932384626433832795028841971f
/*余弦函数(弧度)
angle:      角度（弧度=π*角度/180）*/
double Cosine_Radian(double Radian){
	return Sine_Radian(pi-Radian)
}

正切函数

• 目标
  给一个弧度Number，返回tan(Numberd)的值。

方法一：泰勒展开

先求tanx的泰勒展开式。

y=tanx
y=tan0+(x-0)tan’x/1
?=tan0+xtan’x/1
y=tan0+x[tan0+(x-0)tan’‘x/2]/1
?=tan0+xtan’0/1+x²tan’‘x/2/1
?=tan0+xtan’0/1!+x²tan’‘x/2!
y=tan0+xtan’0/1!+x² [tan0+(x-0)tan’‘‘x/3]/2!
?=tan0+xtan’0/1!+x²tan0/2!+x³tan’’‘x/3!
y=tan0+xtan’0/1!+x²tan0/2!+x³ [tan0+(x-0)tan’‘‘x/4]/3!
?=tan0+xtan’0/1!+x²tan0/2!+x³tan’’‘0/3!+x⁴tan’‘’‘x/4!
… …
y=tan0+xtan’0/1!+x²tan0/2!+x³tan’‘‘0/3!+x⁴tan’’''0/4!+…
?=tan0 + x¹sec²0/1! + 2x²sec²0*tan0/2! + 2x³(2sec²0tan²0 + sec⁴0)/3! +
?8x⁴(sec²0tan³0+2sec⁴0tan0)/4! +…
?=x¹/1!+2x³/3!+16x⁶/5!+272x⁸/7!-7936x¹⁰/9!+…

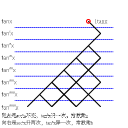
tanx的n次求导后，将0代入的结果有点复杂，要对tanx的导数分析一下。

y=tanx
y’=sec²x
y’‘=2sec²xtanx
y’‘’=4sec²xtan²x+2sec⁴x
y’‘’‘=8sec²xtan³x+16sec⁴tanx
y’‘’‘’=16sec²xtan⁴x+88sec⁴xtan²x+16sec⁶x
…

---

因为将0代入后tan0=0，sec0=1。所以主要分析一下求导后每个项前的常数有什么关系。
0次求导???1
1次求导???1
2次求导???2
3次求导???4+2
4次求导???8+16
5次求导???16+88+16

??在不断求导时。发现每个secⁿxtanⁿx求导时会有两个结果，一个是secⁿx不变，tanⁿ次数加一，另一个就secⁿ次数加二，tanⁿ次数减一，把它简化成一张图就是这样：

??这个图有以下的规律：

• 代码

/*正切函数(弧度)
方法一：泰勒展开求解

taylorLever:        泰勒级数
tempLaver:          临时级数
taylorStore:        泰勒项
taylorBase:         泰勒项的基值
tangent0Value:      泰勒项tan0的Lever次求导后每个项的常数
untie:              解
*/
double tangent_Radian(double Radian){
#define MAXLAVER 40
    double untie=0;
    unsigned short  taylorLever=1,tempLaver;
    // double taylorStore;
    double tangent0Value[MAXLAVER];

    //调整Radian的值到90°~-90°
    if(Radian>pi_2 || Radian<-pi_2){
        Radian+=pi_2;
        tempLaver=Radian/pi;    //调整Radian的值，暂时借用tempLaver变量
        Radian-=tempLaver*pi;
        Radian-=pi_2;
    }

    //初始化
    tangent0Value[0] = Radian;
    Radian*=Radian/2;
    while(taylorLever<MAXLAVER){
        untie += tangent0Value[taylorLever-1];

        //为下次作准备
        for(tempLaver=0;tempLaver<taylorLever+1;tempLaver++){
            if(tempLaver<taylorLever){
                tangent0Value[tempLaver]*=2*(tempLaver+1)*Radian/taylorLever/(taylorLever*2+1);
                if(tempLaver){
                    tangent0Value[tempLaver]+=tangent0Value[tempLaver-1]*(taylorLever-tempLaver+1);
                }
            }
            else{
                tangent0Value[tempLaver]=tangent0Value[tempLaver-1];
            }
        }
        taylorLever++;
    }

    return untie;
}

??经过测试，这个公式的精度并不高，并且当度数接近90度时误差变大，就和柯西中值定理一样，(x-x₀)越大，误差越大。不知道是不是公式推导错了。

方法二：调用正弦余弦函数

tanx=sinx/cosx，所以可以直接用正弦余弦函数。

/*正切函数(弧度)*/
double tangent_Radian(double Radian){
	return Sine_Radian(Radian)/Cosine_Radian(Radian);
}

这个方法虽然有误差，但没有那么大，也不会有度数越大，误差越大的现象。