1. 二叉树的基本结构

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

2. 二叉树的基本函数

2.2 二叉树的构建

对字符串一个一个向后挪动，构建二叉树
运用到了递归（分治）

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	if (a[*pi] == '#'||*pi>=n)
	{
		(* pi)++;//注意不能写出*pi++,不然是*(pi++);
		return NULL;
	}
	BTNode* obj = (BTNode*)malloc(sizeof(BTNode));
	if (obj == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	obj->_data = a[*pi];
	(*pi)++;
	obj->_left = BinaryTreeCreate(a, n, pi);
	obj->_right = BinaryTreeCreate(a, n, pi);
	return obj;
}

2.2 二叉树的销毁

void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
		return;
	BTNode* L = root->_left;
	BTNode* R = root->_right;
	free(root);
	root = NULL;
	BinaryTreeDestory(L);
	BinaryTreeDestory(R);
}

2.3 二叉树的节点个数

算该树左子树节点个数+右子树节点个数+ 1（根）

int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return 1 + BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right);
}

2.4 二叉树的叶子节点个数

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->_left == NULL && root->_right == NULL)
		return 1;
	return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

2.5 二叉树第k层节点个数

思路是算左子树右子树第k-1层节点个数，不断递推到第1层（节点个数肯定为1）

int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

2.6 二叉树查找值为x的节点

分别去左右子树找，两边都没找到返回null，只要有一边不为null则是找到了

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->_data == x)
		return root;
	BTNode* left=BinaryTreeFind(root->_left, x);
	BTNode* right=BinaryTreeFind(root->_right, x);
	if (left == NULL && right == NULL)
		return NULL;
	else
		return right == NULL ? left : right;
}

2.7 二叉树的遍历

分为前序（根左右），中序（左根右），后序（左右根）

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->_data);
	BinaryTreePrevOrder(root->_left);
	BinaryTreePrevOrder(root->_right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	BinaryTreeInOrder(root->_left);
    printf("%c ", root->_data);
	BinaryTreeInOrder(root->_right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	BinaryTreePostOrder(root->_left);
	BinaryTreePostOrder(root->_right);
	printf("%c ", root->_data);
}

3. 二叉树的扩展函数

3.1 二叉树的层序遍历

需要构建一个队列进行辅助
进入一个节点，并把它的左孩子右孩子依次进入队列，之后将队头节点pop
对头节点一直反复以上操作，直到队列为空

//队列的相关函数就不放在这里了
void BinaryTreeLevelOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL\n");
		return;
	}
	Queue Q;
	QueueInit(&Q);
	QueuePush(&Q, root);
	while (!QueueEmpty(&Q))
	{
		printf("%c ", Q.front->x->_data);
		if(Q.front->x->_left!=NULL)
		    QueuePush(&Q, Q.front->x->_left);
		if (Q.front->x->_right != NULL)
		    QueuePush(&Q, Q.front->x->_right);
		QueuePop(&Q);
	}
	QueueDestroy(&Q);
}

3.2 判断是否为完全二叉树

依旧需要一个队列进行辅助
push一个节点，并把它的左孩子和右孩子入队列（不管是否为空），pop出该队头节点
以上操作反复，直到遇到第一个NULL停止，之后判断后面的队列是否全为NULL
不全为NULL则不是完全二叉树

bool BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;
	Queue Q;
	QueueInit(&Q);
	QueuePush(&Q, root);
	while (!QueueEmpty(&Q))
	{
		if (Q.front->x != NULL)
		{
			QueuePush(&Q, Q.front->x->_left);
			QueuePush(&Q, Q.front->x->_right);
			QueuePop(&Q);
		}
		else
			break;
	}
	while (!QueueEmpty(&Q))
	{
		if (Q.front->x != NULL)
		{
			QueueDestroy(&Q);
			return false;
		}
		QueuePop(&Q);
	}
	QueueDestroy(&Q);
	return true;
}

3.3 是否为对称二叉树

在这里插入图片描述

bool judge(struct TreeNode* left,struct TreeNode* right)
{
    if(left==NULL&&right==NULL)
        return true;
    if(left==NULL||right==NULL)
        return false;
    if(left->val!=right->val)
        return false;
    return judge(left->left,right->right)&&judge(left->right,right->left);
}

bool isSymmetric(struct TreeNode* root){
    if(root==NULL)
        return true;
    return judge(root->left,root->right);
}

3.4 判断是否为子树

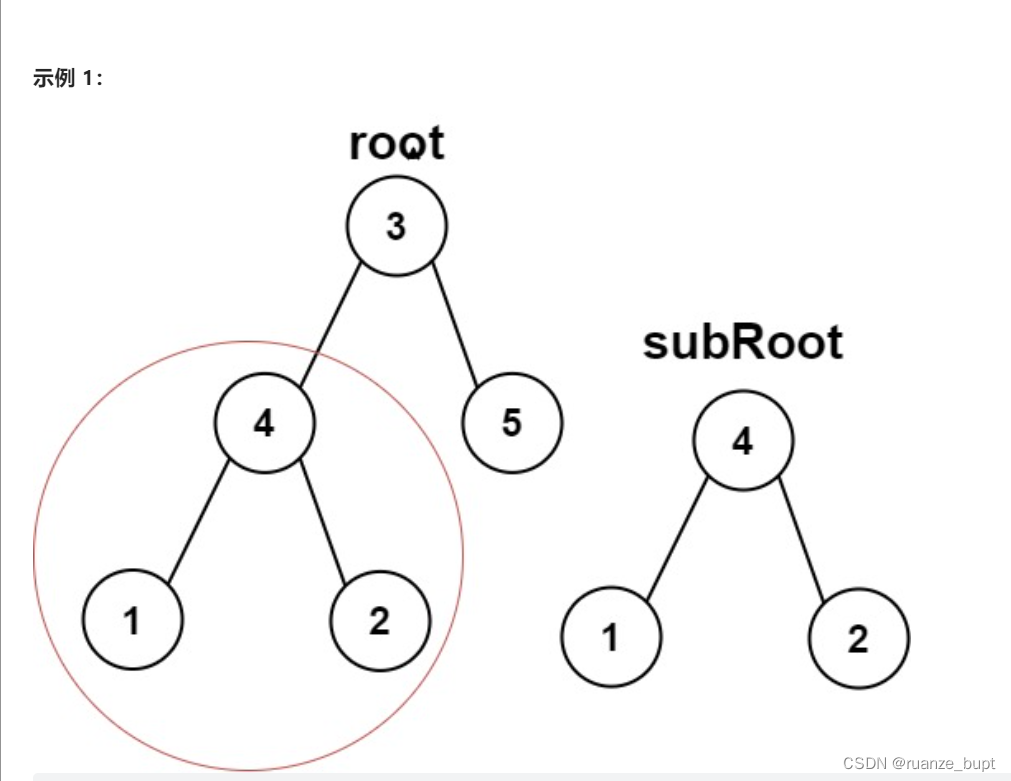
在这里插入图片描述

借助一个判断是否为相同树的函数，然后对根 左孩子 右孩子依次判断

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p==NULL&&q==NULL)
        return true;
    if(p==NULL||q==NULL)
        return false;
    if(p->val!=q->val)
        return false;
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(subRoot==NULL)
        return true;
    if(root==NULL&&subRoot!=NULL)
        return false;
    if(isSameTree(root,subRoot))
        return true;
    return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}