前言

对于二叉树的类型的之间的判断有很多，如判断两个二叉树是否相似、判断一个二叉树是否为完全二叉树、判断一个树是否为排序二叉树…今天就处理以上我说的这些吧！

1 判断两个二叉树是否相似

1.1 做法思路

两个二叉树是否相似，只用看他们是不是相同形状的即可，对于值不要求，因此只要看看两个二叉树每个节点是否存在左右子树即可。
因此可以考虑递归对两个树的节点进行访问。
如果俩节点都不存在，说明相似。
如果一个存在一个不存，说明不相似。
如果俩都存在，则递归遍历他们的子树。
然后俩个子树的返回值取个与就ok/

1.2 具体代码

代码如下（示例）：

bool IsSimilarBiTree(BiTree root1, BiTree root2) {
	if (root1 == NULL && root2 == NULL) {
		return true;
	}
	else if (root1 == NULL || root2 == NULL) {
		return false;
	}
	else {
		bool likel = IsSimilarBiTree(root1->lchild, root2->lchild);
		bool liker= IsSimilarBiTree(root1->rchild, root2->rchild);
		return likel && liker;
	}
}

1.3 测试结果

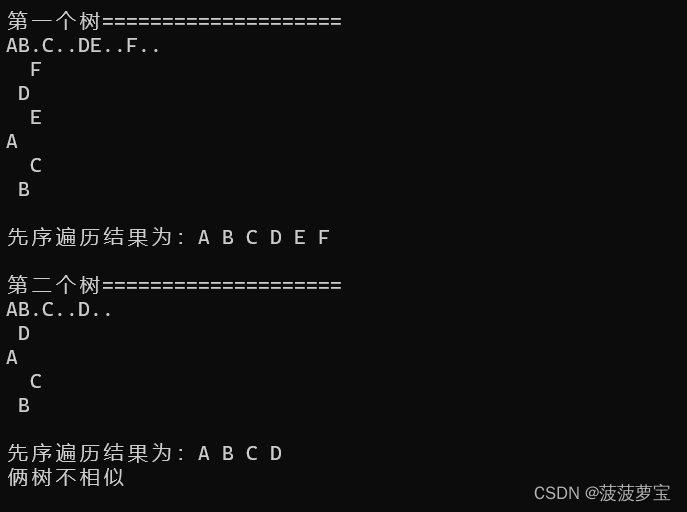
先测试个相似的
在这里插入图片描述
这里建树采用的是先序建树，.的意思是空，建树的时候就是NULL。
显然这里的判断相似是不管值的。
再测试个不相似的

2 判断一个树是否为完全二叉树

2.1 完全二叉树的定义

摘自百度百科：

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

2.2 完全二叉树的性质

摘自百度百科：

1、具有n个结点的完全二叉树的深度（注：[ ]表示向下取整）
2、如果对一棵有n个结点的完全二叉树的结点按层序编号, 则对任一结点i(1≤i≤n) 有:
2.1 如果i=1, 则结点i是二叉树的根, 无双亲;如果i>1, 则其双亲parent (i) 是结点[i/2].
2.2 如果2i>n, 则结点i无左孩子, 否则其左孩子lchild (i) 是结点2i;
2.3 如果2i+1>n,则结点i无右孩子, 否则其右孩子rchild (i) 是结点2i+1.

2.3 判断思路

对于完全二叉树来说，当层次遍历时遍历到NULL时，辅助队列为空，则说明整个树遍历完毕。
如果不是完全二叉树，那么当层次遍历到NULL时，那么辅助队列则不为空。
利用这一点，则可以改写非递归层次遍历来判断一棵树是否为完全二叉树。

2.4 代码改进过程

第一步：首先你得会写非递归层次遍历 =v=

void LayerOrder(BiTree root) {
	if (root == NULL) {
		return;
	}
	Node* cur = root;
	queue< BiTreeNode*>Q;
	Q.push(cur);
	while (!Q.empty()) {
		Node* front = Q.front();
		printf("%c ", front->data);
		Q.pop();
		if (front->lchild != NULL) {
			Q.push(front->lchild);
		}
		if (front->rchild != NULL) {
			Q.push(front->rchild);
		}
	}
	printf("\n");
	return;
}

第二步：改进措施
为了判断是不是完全二叉树，在将节点也就不判断是不是为空，这样出队的时候，即层次遍历到NULL的时候才会判断辅助队列是否为空。
当遍历到为NULL时立刻弹队，如果弹出元素不为空，则说明不是完全二叉树。
如果队列已为空，则说明时完全二叉树。

2.5 具体代码

bool IsCompleteBiTree(BiTree root) {
	if (root == NULL) {
		return 0;
	}
	queue<Node*>Q;
	Node* cur = root;
	Q.push(cur);
	while (!Q.empty()) {
		Node* tmp = Q.front();
		Q.pop();
		if (tmp == NULL) {
			while (!Q.empty()) {
				tmp = Q.front();
				Q.pop();
				if (tmp != NULL) {
					return false;
				}
			}
			return true;
		}
		Q.push(tmp->lchild);
		Q.push(tmp->rchild);
	}
}

2.6 测试结果

测个完全二叉树
建树方法与上面一致，也是.为NULL。先序建树。
在这里插入图片描述
测个非完全二叉树

3 判断一个树是否为排序二叉树

3.1 二叉排序树定义

摘自百度百科：

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。是数据结构中的一类。在一般情况下，查询效率比链表结构要高。

3.2 二叉排序树性质

摘自百度百科：

一棵空树，或者是具有下列性质的二叉树：
（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（3）左、右子树也分别为二叉排序树；
【注】：以上的三种定义在不同的数据结构教材中均有不同的定义方式但是都是正确的在开发时需要根据不同的需求进行选择
【注2】：没有键值相等的结点。

3.3 判断思路

两个思路：
1.可以中序遍历二叉排序树，将结果保存在数组中，判断一个数组是不是递增的即可。
2.递归遍历时保存孩子节点，在遍历的时候将孩子节点的值与当前节点的值进行比较。
遍历时如果该节点不存在，则是二叉排序树。然后从左向右依次遍历，先向左遍历时，如果左子树已经不是二叉排序树或者当前节点小于前一节点（相当于中序遍历，从左往右依次增大，当前节点应当比前一节点大，前一节点也可以理解成线索二叉树中中序遍历的前驱），则返回false。再遍历右子树，返回右子树的判断值即可。
第一种方法比较简单，这里就不实现了。
着重实现一下第二种思路。

3.4 具体代码

bool IsBST(BSTree bst, int* pre) {
	bool bl, br;
	if (bst == NULL) {
		return true;
	}
	else {
		bl = IsBST(bst->lchild, pre);
		if (bl == false || *pre > bst->data) {
			return false;
		}
		*pre = bst->data;//保存中序遍历的前驱
		br = IsBST(bst->rchild, pre);
		return br;
	}
}