[C++知识库]C语言基础—循环语句

1、for 循环

表达式：

for (表达式1; 表达式2; 表达式3)
{
	语句块1;
}

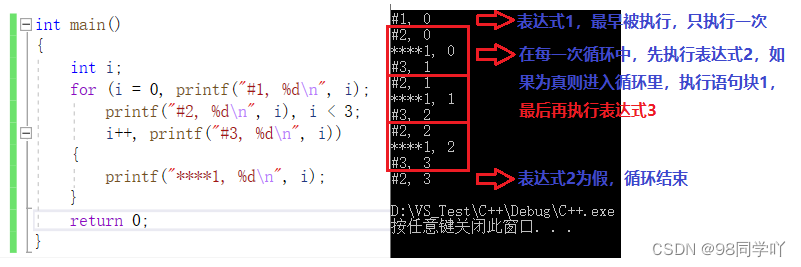
表达式1：初始化，最早被执行，有且执行一次；
表达式2：判断条件，为真循环继续，为假循环结束，每次进入循环都需要判断，每次都执行
表达式3：步进，修改循环因子值，执行完语句块1之后执行，每次都执行

分析如下代码：

例1：

int main()
{
	int i;
	for (i = 0, printf("#1, %d\n", i);
		printf("#2, %d\n", i), i < 3;
		i++, printf("#3, %d\n", i))
	{
		printf("****1, %d\n", i);
	}
	return 0;
}

例2：输出 3 个数字

int main()
{
	int i;
	for (i = 0; i < 3; i++)
	{
		printf("%d\n", i);
	}
	return 0;
}

for 循环中的三个表达式都可以省略（两个分号不能省略），例如上面的程序可以（但是不建议）改成如下代码

int main()
{
	int i = 0;   // 初始化
	for (; ; )
	{
		if (i >= 3) {  // 判断
			break;
		}
		printf("%d\n", i);
		i++;   // 修改循环因子
	}
	return 0;
}

总结：for 循环是使用最多的循环语句，其最大的特点就是三个表达式放在一起，不容易漏写，大家且用且珍惜（●’?’●）

2、while 循环

表达式：

while (表达式1)
{
	语句块1
}

表达式1为真循环继续，为假循环结束

例子：将上面的例子改为 while 循环

int main()
{
	int i = 0;   // 初始化
	while (i < 3) {  // 判断
		printf("%d\n", i);
		i++;   // 修改循环因子
	}
	return 0;
}

3、do while 循环

表达式：

do
{
	语句块1
} while(表达式1);

表达式1为真循环继续，为假循环结束

例子：将上面的例子改成 do while 循环

int main()
{
	int i = 0;   // 初始化
	do {
		printf("%d\n", i);
		i++;   // 修改循环因子
	} while (i < 3);   // 判断条件
	return 0;
}

注意：

• while 保证语句块至少执行 0 次及以上
• do while 保证语句块至少执行 1 次及以上
• 当表达式的第一次的值为 “真” 时，两种循环完全相同

4、break 的使用

break 用于跳出 switch 或者跳出一层循环

例如：求满足如下条件的 x 的值

1 + 2 + 3 + … + x < 1000 且 1 + 2 + 3 + … + x + (x+1) > 1000

输出 x 和求和的值

void SumTo1000()
{
	int sum = 0;   // 保存累加的值
	int i;   // i 后面还需要使用，则定义在 for 循环外面
	for (i = 1; ; i++) {
		sum += i;
		if (sum > 1000) {
			break;   // 符合条件，结束循环
		}
	}
	printf("x = %d, 和 = %d\n", i - 1, sum);
}

输出结果：

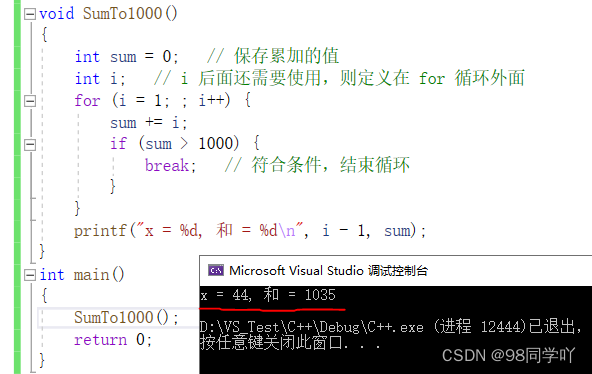
5、continue 的使用

continue：提前结束本次（趟）循环，直接进入下一次（趟）循环

例子：输出 100~200 之间的不能被 3 整除的数

法一：

for (n = 100; n < 200; n++) {
	if (n % 3 != 0) {
		printf("%d  ", n);
	}
}

法二：利用 continue 关键字实现

for (n = 100; n < 200; n++) {
	if (n % 3 == 0) {
		continue;   // 提前结束本次循环，后面的输出不执行
	}
	printf("%d  ", n);
}

6、综合练习

例1：用$\pi /4=1?(1/3+1/5?1/7+...)$ 公式求 $\pi$ 的近似值，直到发现某一项的绝对值小于10^-6 为止

分析：

• 该公式用于求 $\pi /4$，只需要将最后的结果乘以 4 即为 $\pi$ 的值；
• 公式中的每一项均由符号、分子和分母组成，那么在程序中只需要将这三部分处理好

代码如下：

double GetPi()
{
	int flg = 1;   // 保存符号位
	double m = 1;  // 分母
	double n = 1;  // 分子
	double tmp = 0;  // 累加和
	while (n / m > 1e-6) {
		tmp += flg * n / m;
		flg *= -1;
		m += 2;
	}
	return tmp * 4;
}
int main()
{
	double ret = GetPi();
	printf("%lf\n", ret);
	return 0;
}

例2：求斐波那契（Fibonacci）数列的第 n 个数。这个数列有如下特点：第1、第2两个数为 1、1。从第 3 个数开始，该数是前面两个数之和。即：
$$?\begin{array}{ll}{F}_1=1& (n=1)\\ F_2=2& (n=2)\\ F_n=F_{n?1}+F_{n?2}& (n\ge 3)\end{array}$$

int Fibon(int n)
{
	int f1 = 1;   // 保存第一项的值
	int f2 = 1;   // 保存第二项的值
	int f3 = 1;   // 当前项的值
	for (int i = 3; i <= n; ++i) {
		f3 = f1 + f2;   // 当前项的值等于前两项之和
		f1 = f2;   // 还没达到需要求的项数，则两个值需要后移
		f2 = f3;
	}
	return f3;
}
int main()
{
	int n = 3;
	printf("%d\n", Fibon(n));
	return 0;
}