问题描述

序列查询新解题目链接

解题思路

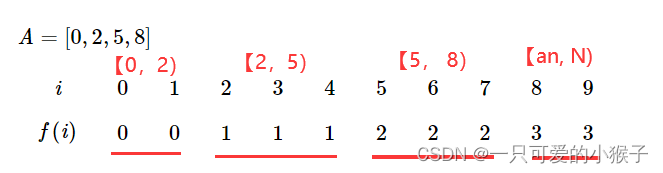
在这里插入图片描述
这个是上一道题目总结出来的规律
就是 f(x) = i 当x属于 【a[i], a[i + 1] ） 这个区间
也就是在这个区间里f(x)都等于一个数i

再看g(x)这个函数，g(x）= x / 常数，也可以知道，g(x)也是单调递增的
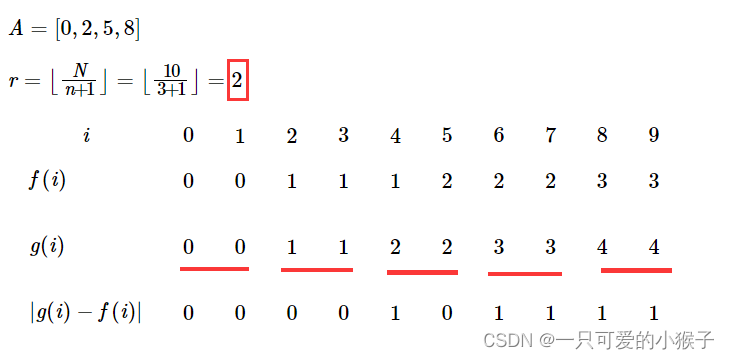
在这里插入图片描述
并且根据规律，可以求得任意g(x)
每一段相同值的g(x)，以i / r为值，长度为 r

我们可以将数组根据f(x）相等，划分为n段
再根据每一段计算差值
又由于f(x）相等的这一段内，g(x）有可能既有比f(x)小，又有比f(x）大的情况，所以直接累加求差是不可取的
所以我们可以在f(x）相等的这一段内，再根据g(x）相等进行划分段，这样划分出来的段，求和做差 == abs（f(x) - g(x)）

然后值得注意的点是
数据很大，要开long long ,不然过不了
在f(x）相等的这一段内，再根据g(x）相等进行划分段，可能存在长度不等于r的段（首尾会出现），所以要计算这个段还剩几个
怎么算？
根据上面那个图的规律可以发现，他就是以r为长度，不断循环，0，1，2 …r - 1
所以当前数x % r就是当前第几个
一段一共有r个，所以还剩r - x % r个
计算出还剩多少个时，要判断是否超出f(x）的长度范围
然后累加计算就行

代码实现

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

int main()
{
    int n;
    long long N;
    cin >> n >> N;
    long long a[n + 10];
    a[0] = 0;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    a[n + 1] = N; //多加上一位，减少特判

    long long res = 0;
    long long r = N / (n + 1);
    for (int i = 0; i <= n; i ++)
    {
        long long res1 = 0, res2 = 0;
        for (long long j = a[i]; j < a[i + 1];)
        {
            long long num = j / r;
            long long cnt = r - j % r;
            cnt = min(cnt, a[i + 1] - j);
            res1 = cnt * i;
            res2 = cnt * num;
            res += abs(res1 - res2);
            j += cnt;
        }
    }
    cout << res;
    return 0;
}