C语言刷题之旅
第一章 C语言刷题(1)
文章目录
前言
本系列内容将对一些C语言的经典题目进行一题多解。
一、二进制位中1的个数
在解决这道题之前,我们先来回顾一下位运算符的运算逻辑:
&——>必须全是1,才是1,否则是0
|——>只要有一个1,就是1,反之为0
^——>相同为0,不同为1
题目描述:
输入一个数字,输出该数字的二进制中1的个数。
题目详解:
法一:
void Number_of_1()
{
int n=0;
int count=0;//记录1的个数
scanf("%d",&n);
for(int i=0;i<32;i++)
{
if((n>>i)&1==1)
{
count++;
}
}
printf("%d",count);
}
思路分析:
当我们将一个数和1做按位和运算的时候,我们会发现如下结果:
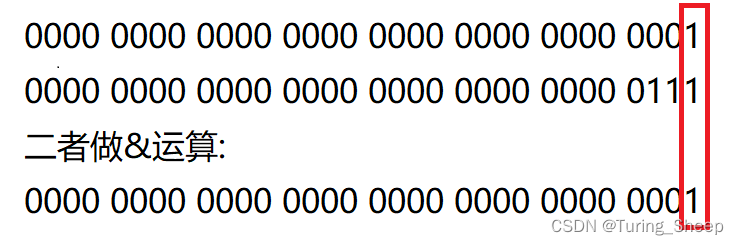
在最低位中,只要原数字中的末位含有1,那么二者做按位和的运算,其结果中的末尾一定含有1.有了这个规律我们只需要将这个数与1做按位和的运算,再右移31次,这样就能够达到将一个数字的每一位都和1做按位和的运算,从而判断原数字的二进制位中1的个数.
那么按位和最终的结果又可以通过什么方式来观察呢?我们发现,如果一个数字的二进制位的最后一位是1那么这个数字就是奇数,否则是偶数.由此我们就能够写出上述的代码.
法二:
void Number_of_1()
{
int n=0;
int count =0;
for(int i=0;i<32;i++)
{
if(n&1==1)
{
count++;
}
n>>=1;
}
printf("%d",count);
}
思路分析:
法一和法二的思路是一致的,只是法1没有改变n本身的数值,但是法2改变了n本身的值.
法三:
void Number_of_1()
{
int n=0;
scanf("%d",&n);
int count=0;
while(n)
{
n=n&(n-1);
count++;
}
printf("%d",count);
}
思路分析:
首先这个方法表面上看起来简单了很多,但是不容易理解,我们以下面的图示来解释这个代码:
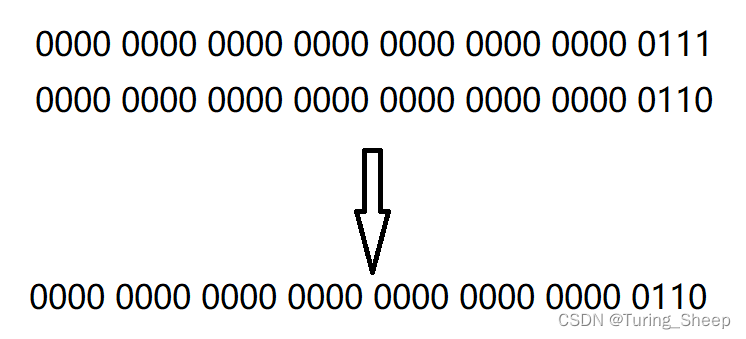
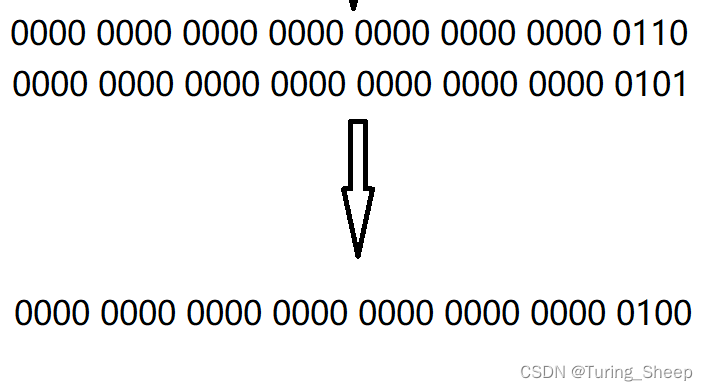
我们将前两行的二进制数字进行按位和运算,最终得到了第三行数字,我们将第三行数字和第一行数字进行对比,我们发现,最终的结果的二进制位中的1的个数减少了1个.也就是说,该运算每进行一次就会减少一个1.最终变成0,结束循环,因此,1的个数就是该循环进行的次数.
法四:
void Number_of_1()
{
unsigned int n=0;//这里一定要输入无符号位
int count =0;
scanf("%d",&n);
while(n)
{
if(n%2==1)
{
count++;
}
n/=2;
}
printf("%d",n);
}
思路分析:
我们曾经可能做过如何拿到一个十进制位的每一位,大体的思路就是先%10再/10.同理,我们要想拿到二进制位的每一位,就可以先%2再/2,这样循环多次,我们就能够拿到一个数二进制位的每一位数字.
但是我们这里非常容易忽略一点:负数
我们知道,当一个数字进行取模运算的时候,倘若这个数字比较小,那么最终取模的结果就是负数本身,这时我们就无法得到1或者0的答案.那我们怎么办呢?
其实我们很容易想到,如果去掉这个数的符号,或许就能够解决这个问题.也就是说我们需要的是一个无符号整型unsigned int类型的数据.
当我们将代码进行上述修改后,确实解决了这个问题,但是!
我们给-1取无符号整型,变成1.而1的二进制位只有1个1,但是我们此时发现最终的结果依旧是32个1,这是为什么呢?要想解决这个问题,我们就需要理解unsigned int的转化本质:
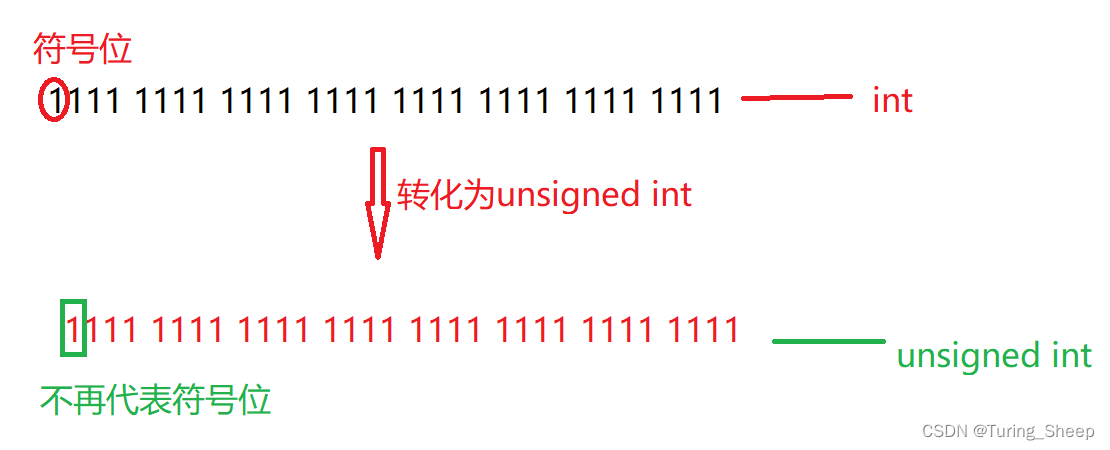
我们发现发生转化后,该数字的二进制位并没有发生变化,仅仅是取消了无符号位的设定,那么该数字此时并不是-1也不是1,而是直接对该数字进行计算,即232次方.
也就是说,从int转化为unsigned int 时,二进制位不发生变化,只是取消了符号位的设定,此时我们也就能够自行计算出unsigned int类型的范围是0-232
二、判断两个数的二进制位的相同位数
题目描述
输入两个值n和m,判断两个数的二进制位中有几位相同, 几位不同。
题目详解
法一:
void test01()
{
int n=0;
int m=0;
int seam=0;
int different=0;
scanf("%d %d",&n,&m);
int a=n^m;
while(a)
{
a=(a-1)&a;
different++;
}
seam=32-different;
printf("两数相同的位有:%d个,不同的位有:%d个",seam,different);
}
我们的位操作符中,除了位移操作符,按位与和按位或,还有一个按位异或,而按位异或的规则是,相同为0不同为1.由此我们就能够计算出一个新的数字,再对这个数字的二进制位的每一位进行判断,就能够得到最终的结果了.
法二:
void test02()
{
int n = 0;
int m = 0;
scanf("%d %d",&n,&m);
int seam = 0;
int different = 0;
for (int i = 0; i < 32; i++)
{
if ((n >> i) == (m >> i))
{
seam++;
}
else
{
different++;
}
}
printf("两数相同的位有:%d个,不同的位有:%d个", seam, different);
}
代码分析:
这种方法和题目一中的思路几乎一致.
三、进制转换
题目描述:
小乐乐在课上学习了二进制八进制与十六进制后,对进制转换产生了浓厚的兴趣。因为他的幸运数字是6,所以他想知道一个数表示为六进制后的结果。请你帮助他解决这个问题.
题目详解:
法1:数组
void test01()
{
int n = 0;
int m = 0;
scanf("%d",&n);
int temp[32] = { 0 };
while (n)
{
temp[m] = n % 6;
n /= 6;
m++;
}
for (int i = m-1; i >=0; i--)
{
printf("%d",temp[i]);
}
}
代码分析:
首先将一个十进制的数字转化为六进制,我们只需要取模6加除法就可以了.但是问题的关键是,如果我们直接输出结果,那么最终打印出的数字是从低位到高位的.而我们想要的结果是从高位到低位,那么我们可以先利用一个恰当的数组去存储这些数据,然后再逆序打印出来.
法二:函数递归
void turn(const int n)
{
if (n > 0)
{
turn(n/6);
printf("%d", n % 6);
}
else
{
return;
}
}
void test02()
{
int n = 0;
scanf("%d",&n);
turn(n);
}
除了数组外,我们还可以采用函数递归的方式进行解答,只是在写递归函数的时候,我们需要注意我们打印和调用函数的顺序.否则会出现打印顺序颠倒的问题,
四.序列中删除指定的数字
题目描述
有一个整数序列(可能有重复的整数),现删除指定的某一个整数,输出删除指定数字之后的序列,序列中未被删除数字的前后位置没有发生改变。
题目详解
法1:
void test03()
{
int n = 0;
int m = 0;
scanf("%d",&n);
scanf("%d", &m);
int arr[n];
int j = 0;
for (int i = 0 ; i < n; i++)
{
scanf("%d",&arr[i]);
if (arr[i] != m)
{
arr[j] = arr[i];
j++;
}
}
for ( int i=0;i<j; i++)
{
printf("%d ",arr[i]);
}
}
这里采用了双指针的方法,我们用下面的图示来解释一下:
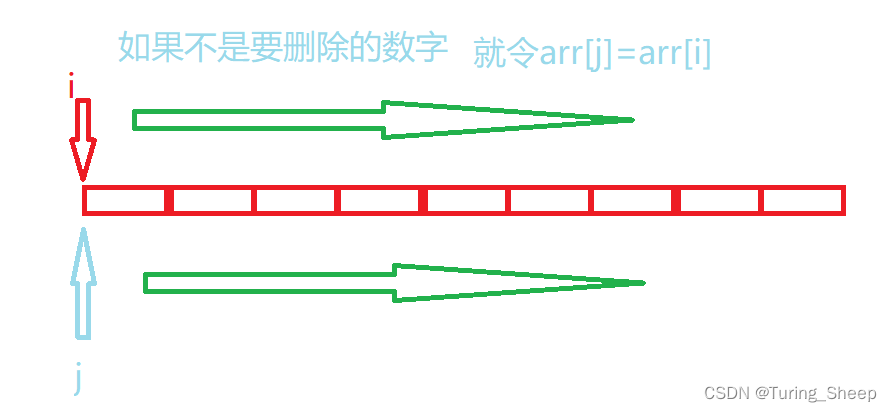
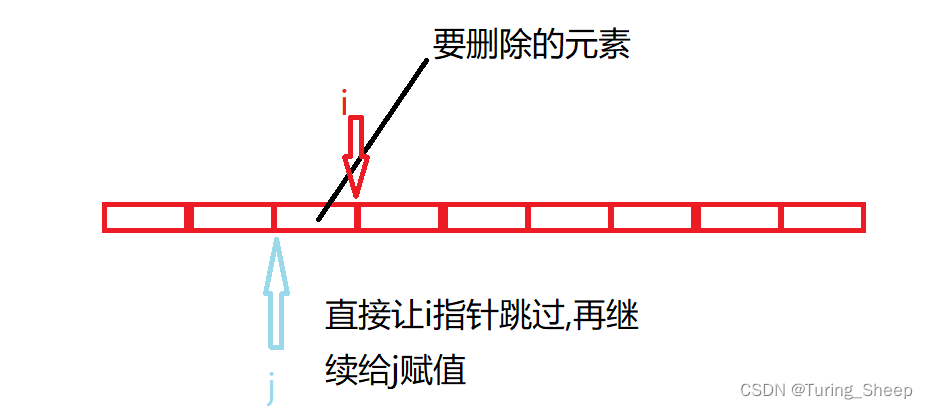
总结
今天所讲解的题目主要围绕着操作符的运算展开的,希望对大家有所帮助.