目录
作者和朋友建立的社区：非科班转码社区-CSDN社区云💖💛💙
期待hxd的支持哈🎉 🎉 🎉
最后是打鸡血环节：你只管努力，剩下的交给天意🚀 🚀 🚀
二叉搜索树概念
二叉搜索树又称二叉排序树，它或者是一棵空树 ，或者是具有以下性质的二叉树 :1. 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值2. 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值3. 它的左右子树也分别为二叉搜索树
二叉搜索树操作
?
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13}; ?
1. 二叉搜索树的查找
a 、从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。b 、最多查找高度次，走到到空，还没找到，这个值不存在。2.?二叉搜索树的插入
插入的具体过程如下：a. 树为空，则直接新增节点，赋值给 root 指针b. 树不空，按二叉搜索树性质查找插入位置，插入新节点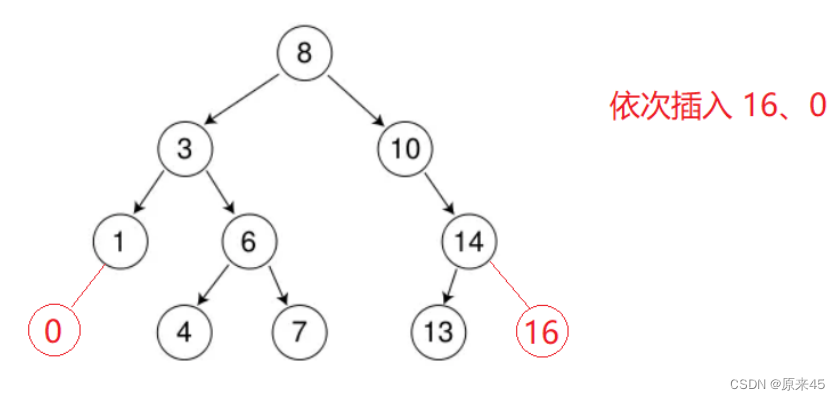
3. 二叉搜索树的删除?
首先查找元素是否在二叉搜索树中，如果不存在，则返回 , 否则要删除的结点可能分下面四种情 况：a. 要删除的结点无孩子结点b. 要删除的结点只有左孩子结点c. 要删除的结点只有右孩子结点d. 要删除的结点有左、右孩子结点实际上a可以属于b或者c
二叉搜索树的应用
1. K模型
K 模型即只有 key 作为关键码，结构中只需要存储 Key 即可，关键码即为需要搜索到 的值 。比如： 给一个单词 word ，判断该单词是否拼写正确 ，具体方式如下：以词库中所有单词集合中的每个单词作为 key ，构建一棵二叉搜索树。在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。2. KV模型
每一个关键码 key ，都有与之对应的值 Value ，即 <Key, Value> 的键值对 。该种方式在现实生活中非常常见：比如 英汉词典就是英文与中文的对应关系 ，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文 <word, chinese> 就构成一种键值对；再比如 统计单词次数 ，统计成功后，给定单词就可快速找到其出现的次数， 单词与其出现次数就是 <word, count> 就构成一种键值对。下面对于KV模型有对应的测试用例
二叉搜索树的性能分析
插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。对有 n 个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：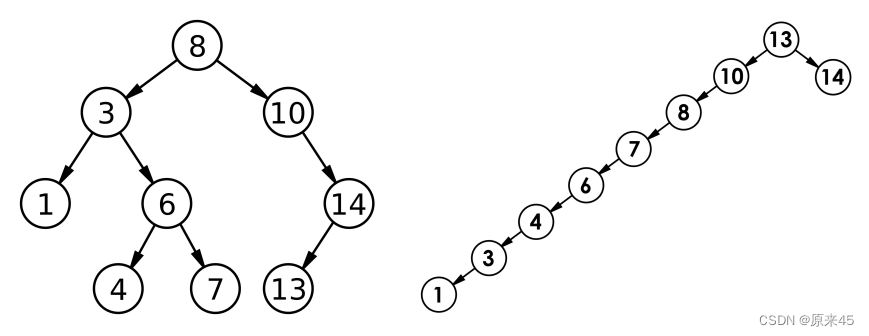
最优情况下，二叉搜索树为完全二叉树 ( 或者接近完全二叉树 ) ，其平均比较次数为： log2 N最差情况下，二叉搜索树退化为单支树 ( 或者类似单支 ) ，其平均比较次数为：N问题：如果退化成单支树，二叉搜索树的性能就失去了。那能否进行改进，不论按照什么次序插入关键码，二叉搜索树的性能都能达到最优？那么我们后续章节学习的AVL 树和红黑树就可以上场了。二叉搜索树也就是为了后面的AVL树和红黑树做铺垫！
二叉搜索树的实现（K&&KV）和测试（KV）
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<string>
using namespace std;
/// //
// K模型
//template<class K>
//struct BSTreeNode {
// BSTreeNode(const K& key)
// :_key(key)
// , _left(nullptr)
// , _right(nullptr)
// {};
//
// BSTreeNode* _left;
// BSTreeNode* _right;
// K _key;
//};
//
//template<class K>
//class BSTree
//{
// typedef BSTreeNode<K> Node;
//public:
// bool Insert(const K& key)
// {
// if (_root == nullptr)
// {
// _root = new Node(key);
// return true;
// }
//
// Node* parent = nullptr;
// Node* cur = _root;
// while (cur)
// {
// if (key > cur->_key)
// {
// parent = cur;
// cur = cur->_right;
// }
// else if (key < cur->_key)
// {
// parent = cur;
// cur = cur->_left;
// }
// else
// {
// return false;
// }
// }
// cur = new Node(key);
// //这里别用nullptr去判断,问就是写的时候好像不对
// if (parent->_key > key)
// {
// parent->_left = cur;
// }
// else
// {
// parent->_right = cur;
// }
// return true;
// }
//
// Node* Find(const K& key)
// {
// Node* cur = _root;
// while (cur)
// {
// if (cur->_key > key)
// {
// cur = cur->_left;
// }
// else if (cur->_key < key)
// {
// cur = cur->_right;
// }
// else
// {
// return cur;
// }
// }
// return false;
// }
//
// //删除有三种情况
// //要删除的孩子有左节点（1）
// //要删除的孩子有右节点（2）
// //要删除的孩子有左，右节点（3）替换法删除
// //要删除的孩子无节点（属于1或2）
// bool Erase(const K& key)
// {
// Node* cur = _root;
// Node* parent = nullptr;
// while (cur)
// {
// if (key < cur->_key)
// {
// parent = cur;
// cur = cur->_left;
// }
// else if (key > cur->_right)
// {
// parent = cur;
// cur = cur->_right;
// }
// else//找到了要删除的节点
// {
// // 一个孩子--左为空 or 右为空
// // 两个孩子 -- 替换法
// if (cur->_left == nullptr)
// {
// if (cur == _root)
// {
// _root = cur->_right;
// }
// else
// {
// if (cur == parent->_left)
// {
// parent->_left = cur->_right;
// }
// else
// {
// parent->_right = cur->_right;
// }
// }
// delete cur;
// }
// else if (cur->_right == nullptr)
// {
// if (cur == _root)
// {
// _root = cur->_left;
// }
// else
// {
// if (cur == parent->_left)
// {
// parent->_left = cur->_left;
// }
// else
// {
// parent->_right = cur->_left;
// }
// }
// delete cur;
// }
// else // 两个孩子都不为空，替换法删除
// //找到左子树的最大节点或者右子树的最小节点替换
// {
// // 右子树的最小节点替代 且右子树最小节点，一定是左，右为空！
// Node* minRight = cur->_right;
// Node* minParent = cur;
// while (minRight->_left)
// {
// minParent = minRight;
// minRight = minRight->_left;
// }
//
// std::swap(cur->_key, minRight->_key);
// if (minParent->_right == minRight)
// {
// minParent->_right = minRight->_right;
// }
// else
// {
// minParent->_left = minRight->_right;
// }
// delete minRight;
// }
// return true;
// }
// }
// return false;
// }
// void _InOrder(Node* root)
// {
// if (root == nullptr)
// return;
//
// _InOrder(root->_left);
// cout << root->_key << " ";
// _InOrder(root->_right);
// }
// void InOrder()
// {
// _InOrder(_root);
// }
//private:
// Node* _root = nullptr;
//};
//
//int main()
//{
// BSTree<int> bs;
// bs.Insert(3);
// bs.Insert(8);
// bs.Insert(7);
// bs.Insert(9);
// bs.Insert(11);
//
// bs.InOrder();
// return 0;
//}
/// //
// K V模型
template<class K,class V>
struct BSTreeNode {
BSTreeNode(const K& key,const V& value)
:_key(key)
,_value(value)
, _left(nullptr)
, _right(nullptr)
{};
BSTreeNode* _left;
BSTreeNode* _right;
K _key;
V _value;
};
template<class K,class V>
class BSTree
{
typedef BSTreeNode<K,V> Node;
public:
bool Insert(const K& key,const V& value)
{
if (_root == nullptr)
{
_root = new Node(key,value);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
//这里别用nullptr去判断,问就是写的时候好像不对
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return nullptr;
}
//删除有三种情况
//要删除的孩子有左节点（1）
//要删除的孩子有右节点（2）
//要删除的孩子有左，右节点（3）替换法删除
//要删除的孩子无节点（属于1或2）
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_right)
{
parent = cur;
cur = cur->_right;
}
else//找到了要删除的节点
{
// 一个孩子--左为空 or 右为空
// 两个孩子 -- 替换法
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else // 两个孩子都不为空，替换法删除
//找到左子树的最大节点或者右子树的最小节点替换
{
// 右子树的最小节点替代 且右子树最小节点，一定是左，右为空！
Node* minRight = cur->_right;
Node* minParent = cur;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
std::swap(cur->_key, minRight->_key);
if (minParent->_right == minRight)
{
minParent->_right = minRight->_right;
}
else
{
minParent->_left = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ": " << root->_value << endl;
_InOrder(root->_right);
}
void InOrder()
{
_InOrder(_root);
}
private:
Node* _root = nullptr;
};
void TestBSTree()
{
//BSTree<string,string> dict;
//dict.Insert("insert", "插入");
//dict.Insert("erase", "删除");
//dict.Insert("left", "左边");
//dict.Insert("string", "字符串");
//string str;
//while (cin >> str)
//{
// auto ret = dict.Find(str);
// if (ret)
// {
// cout << str << ":" << ret->_value << endl;
// }
// else
// {
// cout << "单词拼写错误" << endl;
// }
//}
string strs[] = { "苹果", "西瓜", "苹果", "樱桃", "苹果", "樱桃", "苹果", "樱桃", "苹果" };
// 统计水果出现的次
BSTree<string,int> countTree;
for (int i = 0; i < sizeof(strs) / sizeof(strs[0]); i++)
{
auto ret = countTree.Find(strs[i]);
if (ret == nullptr)
{
countTree.Insert(strs[i], 1);
}
else
{
ret->_value++;
}
}
countTree.InOrder();
//for (auto str : strs)
//{
// auto ret = countTree.Find(str);
// if (ret == NULL)
// {
// countTree.Insert(str, 1);
// }
// else
// {
// ret->_value++;
// }
//}
//countTree.InOrder();
}
int main()
{
TestBSTree();
return 0;
}
最后的最后，创作不易，希望读者三连支持💖
赠人玫瑰，手有余香💖