一个数组中只有两个数字是出现一次,其他所有数字都出现了两次。
1.明确题目意思
首先,题目是,一个数组中有两个数字是出现了一次的,其他所有数字出现了两次。
举个具体例子如下
int arr[] = {5,6,6,8,8,9,9,7};
观察一下,这个数组中只有5和7出现了一次,而其他数分别出现了两次。
让我们在不知道的具体数组情况下,求出5和7。
2.与解题思路有关的一些知识
这种题目可以用暴力求解,但是我们这里不用暴力求解。
我们用**按位异或(^)**的知识进行求解
先了解按位异或的几个小知识
我们知道 异或是 “相同为0,不同为1”。
在这里我给大家一个全新的异或理解,那就是无进位相加。,意思就是每个二进制相加了以后不进位。
比如 4 ^ 5
4的二进制是 00000100
5的二进制是 00000101
对应的二进制无进位相加就是 00000001
我们再来拿刚才4 ^ 5的二进制位再次异或5
4 ^ 5 ^5
4^5:00000001
5: 00000101
异或后得到结果就是00000100 这个值是4
那我们拿4^5的结果异或4呢?
4^5: 00000001
4: 00000100
得到的结果是00000101,得到的结果是5
你会发现 4 ^ 5 ^ 5 = 4
4 ^ 5 ^ 4 = 5
如果是2^2^2^2^3^3^3,你猜一下等于几?
是的等于3
结论:
一个数组中的数全部拿来异或,出现了偶数次的数全部异或为0,出现了奇数次的数只剩下它本身。
很难理解的话,我们可以用无进位相加理解
比如2的二进制是00000010
2^2就是
00000010
00000010
无进位相加,就是00000000
再异或一次2,就是
2 ^ 2 ^ 2
00000000
00000010
结果为00000010,结果回来了,还是2
无进位相加就是相加了没有进位,利用这个特征,我们可以知道,只要两两对应的比特位出现偶数次相同的数,我们都可以把他这个数算成0,出现奇数次,那就只剩下一个。
再来看一个例子

3.解题思路
有了前面的知识铺垫,那我们的解题思路就很好理解了。
在做题目这道题之前,我们来看与这道题类似的一道题目。
一个数组中有一个数字出现了奇数次,其他所有数字出现了偶数次。
比如int arr[] = {2,3,3,4,4,5,5};
是不是很简单,直接拿数组进行异或就好了。
而我们这道题是:
一个数组中只有两个数字是出现一次,其他所有数字都出现了两次。
一次指的就是奇数次,两次指的就是偶数次。异或的效果都一样。
可是如果用之前的思路全部拿来异或的话,得到的结果就是
这两个出现一次的数字的异或结果,记为eor=a^b
别急。
我们好好想一想,如果两个数异或不为0的话,是不是说明这两个数肯定不相等,既然不相等,是不是说明至少有一个二进制位不相等。
那我们就可以拿那个不相等的二进制位展开思路。
两个数某一个二进制位不相等,一个要么为1,另一个要么为0
那么我们可以利用这一点做区分,分为两组,
一组是某一个二进制位为1的数,一组是某一个二进制位为0的数
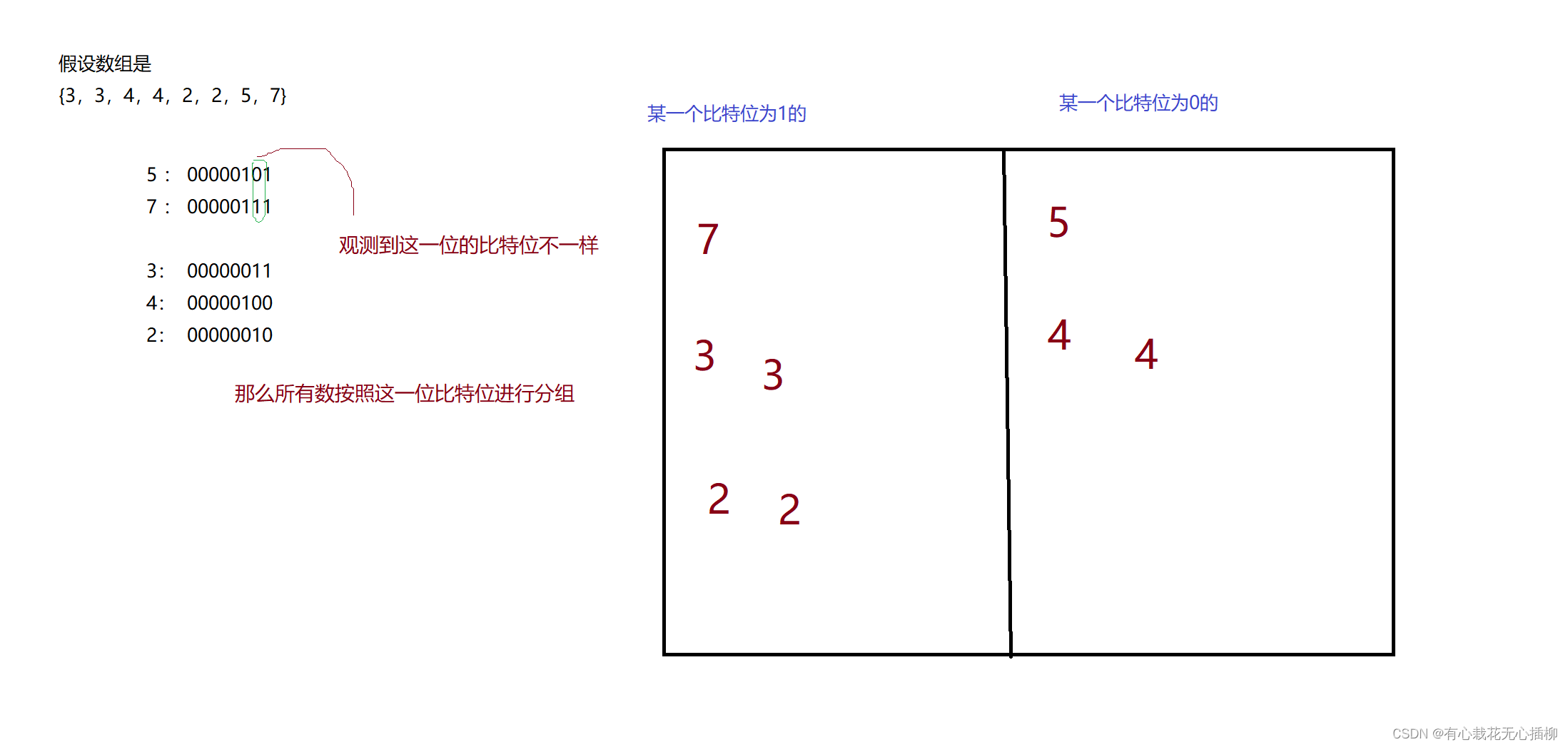
只要我们把其中一组一直异或下去,就可以得到那个只出现一次的数,记为eor2 = a,然后再拿 eor ^ eor2 = a ^ b ^ a = b
就可以求出这两个数了。
4.具体代码
//一个数组中只有两个数字是出现一次,其他所有数字都出现了两次。
//编写一个函数找出这两个只出现一次的数字。
#include <stdio.h>
void FindTwoNum(char arr[],int sz)
{
int eor = 0;
for (int i = 0; i < sz; i++)
{
eor ^= arr[i];
//这个eor的最终结果必然是那两个数的异或的结果,记为a^b
} //a和b必然有一个二进制位不同
int onlyone = eor & (~eor + 1);//一个原码按位与上自己的补码,
//得到的数是某一个二进制位为1的数,
//其他二进制位为0
//我们可以利用这个确定哪一个二进制位不同
int eor2 = 0;
for (int i = 0; i < sz; i++)
{
if ((arr[i] & onlyone) == 0)
{
eor2 ^= arr[i];
//把某一位为二进制为0的数,异或进eor2里面,
//一直异或下去,会得到那两个数其中一个数
}
}
printf("%d %d", eor2, eor2 ^ eor);
//得到一个数a以后,在拿a ^ (a ^ b),得到另外一个数
}
int main()
{
int arr[] = { 5,3,3,2,2,4,4,7 };
FindTwoNum(arr, sizeof(arr));
return 0;
}