[C++知识库]概率论与梳理统计学习：随机变量（二）——知识总结与C语言案例实现

hello，大家好。

这里是第四期概率论与数理统计的学习，我将用这篇博客去整理知识点以及用C语言去实现案例。

还是先总结一遍这期的知识点。

💦 连续型随机变量与随机变量的分布函数

在上一期的学习中，我们总结了离散型随机变量的定义和它的概率分布，同时我们也提到了一个随机变量的概念——连续型随机变量。

在前面我们给出离散型随机变量的特点是不连续，所以连续型随机变量的特点也就是连续了。但是，最开始的时候我一直没搞懂“连续”的含义是什么，离散型随机变量哪里不连续了？连续性随机变量哪里连续了？别着急，慢慢往下看。

?? 概率密度函数

🌱 定义：若存在非负函数$f(x)$，使随机变量取之于任一区间$(a,b]$的概率可以表示为 P { a < X ≤ b } = ∫ a b f ( x ) d x P\{a<X\leq b\}=\int_{a}^{b}f(x)dx P{a<X≤b}=∫ab?f(x)dx，则称$X$为连续型随机变量，$f(x)$为$X$的概率密度函数，简称概率密度。

从上面这段定义中，你是否能看出离散型与连续型的区别？如果把试验的结果看作一个区间的话，离散型随机变量可以说是这个区间上的某个点，而连续型随机变量就是这个区间上的一个子区间（但不能是一个点），此即“连续”。别急，继续往下看。

🌱 概率密度函数的性质：

1. ${\int }_{?\infty }^{+\infty }f(x)dx=1$
2. 对连续型随机变量$X$和任意常数$a$，总有 P { X = a } = 0 P\{X=a\}=0 P{X=a}=0

第一条比较好理解，第二条性质是个啥意思？

假定给定区间$[0,1]$，对其中任意一点$a$，有 P { X = a } = 0.01 P\{X=a\}=0.01 P{X=a}=0.01，这么一看貌似没问题，但就这么一个小区间，也可以分成无数个点，最后加起来的概率肯定大于1，所以才有了性质2。

但性质2同时也说明：$P(A)=0$，并不可能推出$A$是不可能事件，因为在这里虽然 P { X = a } = 0 P\{X=a\}=0 P{X=a}=0，但事件 { X = a } \{X=a\} {X=a}并非不可能事件。

于是，连续型随机变量$X$落在区间$(a,b),(a,b],[a,b),[a,b]$上的概率都相等，即 P { a < X < b } = P { a ≤ X < b } = P { a < X ≤ b } = P { a ≤ X ≤ b } P\{a<X<b\}=P\{a\leq X<b\}=P\{a<X\leq b\}=P\{a\leq X\leq b\} P{a<X<b}=P{a≤X<b}=P{a<X≤b}=P{a≤X≤b}

?? 常见的连续型随机变量的概率密度函数

?? 均匀分布

如果随机变量$X$的概率密度函数为$$f(x)=\{\begin{array}{l}\frac{1}{b?a},a\le x\le b\\ 0,其它\end{array}$$
则称$X$服从$[a,b]$区间上的均匀分布，记作$X$~$U[a,b]$（$U$取自Uniform，均匀）。

对于任意长度为$l$的子区间$[c,c+l],a\le c<c+l\le d$，有 P { c ≤ X ≤ c + l } = ∫ c c + l f ( x ) d x = l b ? a P\{c\leq X\leq c+l\}=\int_{c}^{c+l}f(x)dx=\frac{l}{b-a} P{c≤X≤c+l}=∫cc+l?f(x)dx=b?al?

?? 指数分布

如果随机变量$X$的概率密度函数为$$f(x)=\{\begin{array}{l}\lambda e^{?\lambda x},x\ge 0\\ 0,x<0\end{array}$$
其中$\lambda >0$为常数，则称$X$服从参数为$\lambda$的指数分布。指数分布是最常用的寿命分布。
有$${\int }_{?\infty }^{+\infty }f(x)dx={\int }_{?\infty }^{+\infty }\lambda e^{?\lambda x}dx=1$$

?? 正态分布

设随机变量$X$的概率密度函数为$$f(x)=\frac{1}{\sqrt[]{2\pi }\sigma }{e}^{?\frac{(x?\mu {)}^2}{2{\sigma }^2}},?\infty <x<+\infty$$

其中，$\mu ,\sigma$为常数，则称$X$服从参数为$\mu ,\sigma$的正态分布或高斯分布，记为$X$~$N(\mu ,{\sigma }^2)$，这里$N$取自Normal。

正态分布的概率密度函数$f(x)$图如下👇：

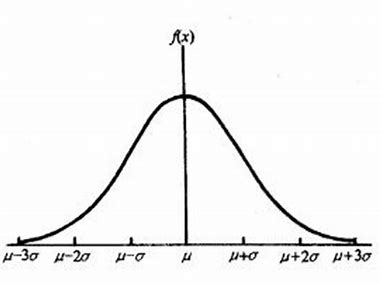
它有如下性质：

🌱 关于直线$x=\mu$对称

🌱 在$x=\mu$处取得最大值$\frac{1}{\sqrt[]{2\pi }\sigma }$

🌱 在$x=\underline{+}\sigma$处有拐点

🌱 当$|x|\to +\infty$时，曲线以$x$轴为渐近线

特别地，称参数$\mu =0,\sigma =1$的正态分布$N(0,1)$为标准正态分布，其概率密度函数通常用$\psi (x)$来表示，即$$\psi (x)=\frac{1}{\sqrt[]{2\pi }}{e}^{?\frac{x^2}{2}},?\infty <x<+\infty$$
此外，记$$?(x)=\frac{1}{\sqrt[]{2\pi }}{\int }_{?\infty }^x{e}^{?\frac{t^2}{2}}dt,?\infty <x<+\infty$$
由$\psi (x)$的对称性，可推出$?(x)$的如下性质：$$?(?x)=1??(x)$$

🌱 定理：

若随机变量$X$~$N(\mu ,{\sigma }^2)$，则对任意$a,b(a<b)$，有 P { a < X ≤ b } = ? ( b ? μ σ ) ? ? ( a ? μ σ ) P\{a< X\leq b\}=\phi(\frac{b-\mu}\sigma)-\phi(\frac{a-\mu}\sigma) P{a<X≤b}=?(σb?μ?)??(σa?μ?)

?? 随机变量的分布函数

🌱 定义：

设$X$是一随机变量，称函数 F ( x ) = P { X ≤ x } , ? ∞ < x < + ∞ F(x)=P\{X\leq x\},-\infty <x<+\infty F(x)=P{X≤x},?∞<x<+∞为$X$的分布函数。

随机变量的分布函数有如下性质：

🌱 对任意实数$a<b$，总有$F(a)\le F(b)$，并且 P { a < X ≤ b } = F ( b ) ? F ( a ) P\{a<X\leq b\}=F(b)-F(a) P{a<X≤b}=F(b)?F(a)

🌱 对任意实数$x$，总有$0\le F(x)\le 1$，且$F(?\infty )=\underset{x\to ?\infty }{\lim }F(x)=0,F(+\infty )=\underset{x\to +\infty }{\lim }F(x)=1$

🌱 P { X < a } = F ( a ? 0 ) P\{X<a\}=F(a-0) P{X<a}=F(a?0)，$a?0$表示从左逼近$a$，但不包含$a$。

🌱 P { X > a } = 1 ? P { X ≤ a } = 1 ? F ( a ) P\{X>a\}=1-P\{X\leq a\}=1-F(a) P{X>a}=1?P{X≤a}=1?F(a)

🌱 P { X = a } = F ( a ) ? F ( a ? 0 ) P\{X=a\}=F(a)-F(a-0) P{X=a}=F(a)?F(a?0)

注意??上面的分布函数适用于离散型和连续型，只有连续型随机变量中，开闭区间才等同。

对离散型随机变量$X$，由概率的可加性可得 F ( x ) = P { X ≤ x } = ∑ x k ≤ x P { X = x k } F(x)=P\{X\leq x\}=\sum_{x_{k}\leq x}P\{X=x_{k}\} F(x)=P{X≤x}=xk?≤x∑?P{X=xk?}

基础知识预备完毕，下面开始C语言案例实现！

💦 C语言案例实现

在开始之前，先实现三种常见的连续型随机变量的概率密度函数的算法。

🌱 均匀分布：

#include <stdio.h>
#include <stdlib.h>
// we assume that c,d,must be in the section [a,b] and c <= d
// 我们假定c，d一定在区间[a,b]中且一定有c<=d
void UniDistrubution(float a,float b,float c,float d)
{
	// for continuous random variables
	if(c == d)
	{
		printf("The possibility of the incident you expect is 0.");
		exit(0);
	}
	float PX;
	PX = (d - c) / (b - a);
	printf("The possibility of the incident X is :%f",PX);
}
int main()
{
	UniDistrubution(-2,4,3,4);
	return 0;
}

🌱 指数分布：

设某电子管的使用寿命$X$（单位：小时）服从参数$\lambda =0.0002$的指数分布。求电子管的使用寿命超过3000小时的概率。

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
float Figure_e(int n)
{
	float e = 1;
	int sum = 1;
	for(int i = 1 ; i <= n ; i++)
	{
		sum *= i;
		e += 1.0 / sum;
	}
	return e;
}

// x1 denotes the lower limit of integral ——x1代表积分下限
// x2 denotes the upper limit of integral ——x2代表积分上限
// w denotes the parameter λ ——w代表参数λ
float ExDistrubution(float x1,float x2,float w)
{
	// X1 denotes the value that the lower limit brings in when the function is integrated ——X1表示函数被积分后下限带进去的值
	// X2 is the same ——X2同理
	float X1,X2;
	if(x1 < 0 || x2 < 0)
	{
		printf("The possibility of the incident you expect is 0.");
		exit(0);
	}
	// e denotes the natural number e ——e表示自然数e
	float e = Figure_e(10);
	X1 = pow(e,-w*x1);
	// 32767 denotes positive infinity ——32767表示正无穷
	if(x2 == 32767)
		X2 = 0;
	else
		X2 = pow(e,-w*x2);
	float PX = X1 - X2;
	return PX;	
}

int main()
{
	float x1 = 3000;
	float x2 = 32767;
	float w = 0.0002;
	float P = ExDistrubution(x1,x2,w);
	printf("%.4f",P);
	return 0;
}

这些值都是我用书上例题带进去的！！

🌱 正态分布

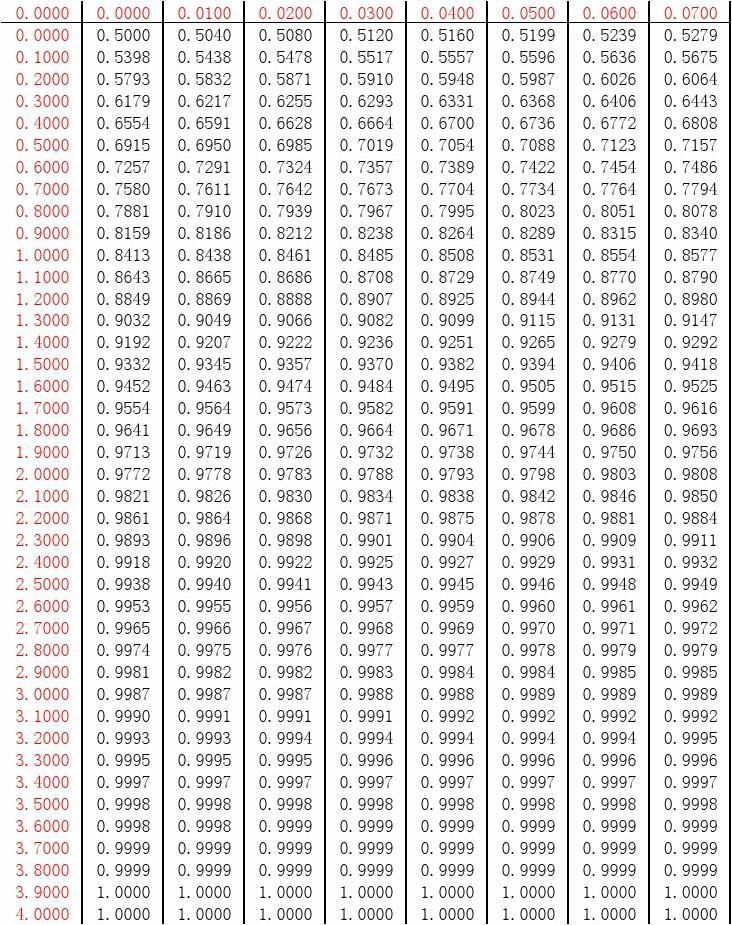
因为正态分布涉及到对$e^{?\frac{t^2}{2}}$的求积分，而它的原函数是求不出来的，需要做一些变化。em…也就是用C语言实现起来很困难，所以这里对于正态分布的题就直接查表即可。标准正态分布表如下（横纵坐标都是$x$）👇：
$$?(x)={\int }_{?\infty }^x\frac{1}{\sqrt[]{2\pi }}{e}^{?\frac{u^2}{2}}du$$

已知某台机器生产的螺栓长度$X$（单位：厘米）服从参数$\mu =10.05,\sigma =0.06$的正态分布。规定螺栓长度在$10.05\underline{+}0.12$内为合格产品，试求螺栓为合格品的概率。

假设$X$~$N(10.05,0.06^2)$，记$a=10.05?0.12,b=10.05+0.12$。又因为正态分布是连续型随机变量的概率密度函数，所以开闭区间都一样，就有 P { a ≤ X ≤ b } = P { a < X ≤ b } P\{a\leq X\leq b\}=P\{a<X\leq b\} P{a≤X≤b}=P{a<X≤b}。

于是：

P { x < X ≤ b } P\{x<X\leq b\} P{x<X≤b}
$=?(\frac{b?\mu }{\sigma })??(\frac{a?\mu }{\sigma })$
$=?(2)??(?2)$
$=?(2)?[1??(2)]$
$=2?(2)?1$

再根据商标可知，当$x=2$时，$?(x)=0.9772$。所以答案也就显而易见了。

1. 某种元件的寿命$X$（单位：小时）的概率密度函数为：
   $$f(x)=\{\begin{array}{l}\frac{1000}{x^2},x\ge 1000\\ 0,x<1000\end{array}$$
   求5个元件在使用1500小时后，恰有2个元件失效的概率。

分析：有两个元件在使用1500小时后失效，也就是它们的使用寿命不超过1500小时。这里不需要考虑它们使用寿命小于1000的情况，因为小1000的概率为0。所以，我们首先需要求的是一个元件使用寿命在1000~1500的概率。
即${\int }_{1000}^{1500}f(x)dx=?$

#include <stdio.h>
float AfIntegral(float x)
{
	// the integrated function ——积分后的函数
	x = -1000 / x;
	return x;
}
int main()
{
	float p;
	p = AfIntegral(1500) - AfIntegral(1000);
	printf("%f",p);
	return 0;
}

然后这个题就变成了一个离散型随机变量的二项分布：

#include <stdio.h>

float AfIntegral(float x)
{
	x = -1000 / x;
	return x;
}

// 组合算法
int Combination(int n,int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}
	return sum/p;
}

// 二项分布算法
float BinDistrubution(int n,int k,float p)
{
	float _P;
	_P = Combination(n,k);
	for(int i = 0 ; i < k ; i++)
		_P *= p;
	for(int i = 0 ; i < n - k ; i++)
		_P *= (1 - p);
	return _P;
}

int main()
{
	float p;
	p = AfIntegral(1500) - AfIntegral(1000);
	float _P = BinDistrubution(5,2,p);
	printf("%f",_P);
	return 0;
}

这个概率呢也就是$\frac{80}{243}$，做题中一般没有化成小数。

2. 设某地区每天的用电量$X$（单位：百万千瓦·时）是一连续型随机变量，概率密度函数为$$f(x)=\{\begin{array}{l}12x(1?x{)}^2,0<x<1\\ 0,其它\end{array}$$
   假设该地区每天的供电量仅有80万瓦·时，求该地区每条供电量不足的概率。若每条上升到90万千瓦·时，每天供电量不足的概率是多少？

分析1）：首先要注意题目给出的单位！！一个是百万瓦，一个是万瓦，记得换算！！

什么叫供电量不足？我们只有80的供电量，但我们一天至少要100的供电量，这就是不足，也就是$0<x<0.8$的情况。这个题相较于上面那个题就只根据概率密度函数求一个概率就是了。

#include <stdio.h>
#include <math.h>
// 这个函数是题目中函数积分后的算法
float AfIntegral(float x)
{
	float a = 3 * pow(x,4);
	a -= 8 * pow(x,3);
	a += 6 * pow(x,2);
	return a;
}

int main()
{
	float p = AfIntegral(1) - AfIntegral(0.8);
	printf("%f",p);
	return 0;
}

2. 第二问呢只需要改变一下积分区间即可：

#include <stdio.h>
#include <math.h>
float AfIntegral(float x)
{
	float a = 3 * pow(x,4);
	a -= 8 * pow(x,3);
	a += 6 * pow(x,2);
	return a;
}

int main()
{
	float p = AfIntegral(1) - AfIntegral(0.9);
	printf("%f",p);
	return 0;
}

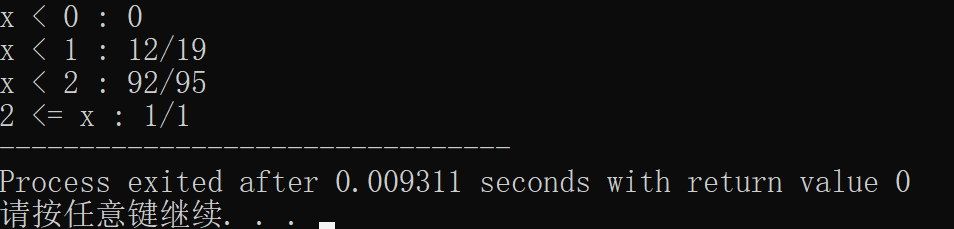
3. 20件同类型的产品中有2件次品，其余为正品。今从这20件产品中任意抽取4次，每次只取一件，取后不放回。以$X$表示4次共取出次品的件数，求$X$的概率分布与分布函数。

分析：概率分布就是列一张表，列出抽到或没抽到次品的概率。分布函数是随机变量的分布函数。嗯…上一次这么解释还是在上一次啊

好吧，分布函数，就是随机变量分布在一个区间内的概率。

首先，$X$的取值有3种可能，分别是0，1，2

#include <stdio.h>
// 约分函数
void Abbreviation(long int *a)
{
	while(a[0] % 2 == 0 && a[1] % 2 == 0)
	{
		a[0] /= 2;
		a[1] /= 2;
	}
	
	for(int i = 3 ;i < a[1] / 2 ; i += 2)
	{
		while(a[0] % i == 0 && a[1] % i == 0)
		{
			a[0] /= i;
			a[1] /= i;
		}
	}
}

int Combination(int n,int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}
	return sum/p;
}

int main()
{
	// the number of the quality goods ——正品的数量
	int real = 18;
	// the number of the defective goods ——次品的数量
	int fake = 2;
	// the number of the defective goods I've extracted ——每次抽到次品的数量
	int pos = 0;
	for(int i = 0 ; i < 3 ; i++)
	{
		// the target to use the array is to do the reduction of a fraction ——用数组是为了方便后面的约分
		long int a[2];
		a[0] = Combination(real,4 - pos) * Combination(fake,pos);
		a[1] = Combination(real + fake,4);
		Abbreviation(a);
		printf("The possibility of X=%d is : %d/%d\n",i,a[0],a[1]);
		pos++;
	}
	return 0;
}

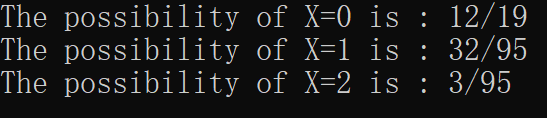
然后就是求它的分布函数，由于涉及到分数形式的概率相加，还需要通分，也就是得要有一个通分函数啊

由$X$的取值可知，我们可以将它的取值划分为4个区间，分别是：
$x<0$
$0\le x<1$
$1\le x<2$
$2\le x$
注意这里$x$和$X$的区别。现在可以往上翻再看看分布函数的概念。例如，当$1\le x<2$时， F ( x ) = P { X ≤ x } F(x) = P\{X\leq x\} F(x)=P{X≤x}，也就是$F(x)$等于小于$x$的所有$X$的概率之和。即上面条件下， F ( x ) = P { X = 0 } + P { X = 1 } F(x)=P\{X= 0\}+P\{X=1\} F(x)=P{X=0}+P{X=1}

那么进而：

#include <stdio.h>
// 约分函数
void Abbreviation(long int *a)
{
	while(a[0] % 2 == 0 && a[1] % 2 == 0)
	{
		a[0] /= 2;
		a[1] /= 2;
	}
	
	for(int i = 3 ;i < a[1] / 2 ; i += 2)
	{
		while(a[0] % i == 0 && a[1] % i == 0)
		{
			a[0] /= i;
			a[1] /= i;
		}
	}
}

int Combination(int n,int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}
	return sum/p;
}

int main()
{
	// the number of the quality goods ——正品的数量
	int real = 18;
	// the number of the defective goods ——次品的数量
	int fake = 2;
	// the number of the defective goods I've extracted ——每次抽到次品的数量
	int pos = 0;
	int j = 0;
	long int a[6];
	for(int i = 0 ; i < 3 ; i++)
	{
		// the target to use the array is to do the reduction of a fraction ——用数组是为了方便后面的约分
		a[j++] = Combination(real,4 - pos) * Combination(fake,pos);
		a[j++] = Combination(real + fake,4);
		Abbreviation(a + i * 2);
		pos++;
	}
	j = 0;
	// use array b to record the score ——用数组b来记录分数（每个概率）
	long int b[2] = {0};
	int k = 3;
	while(j <= 3)
	{
		if(b[0] == 0)
		{
			printf("x < %d : %d\n",j++,b[0]);
			b[0] += a[0];
			b[1] += a[1];
			printf("x < %d : %d/%d\n",j++,b[0],b[1]);
			continue;
		}
		int n = b[1];
		b[1] *= a[k];
		b[0] *= a[k];
		b[0] += a[k - 1] * n;
		Abbreviation(b);
		if(j == 3)
		{
			printf("2 <= x : %d/%d",b[0],b[1]);
			j++;
			continue;
		}
		printf("x < %d : %d/%d\n",j++,b[0],b[1]); 
		k += 2;
	}
	return 0;
}

好啦这期学习就到这里了，下期，如有不足之处，希望大家能多多指正