想必汉诺塔的那几句简单的代码让我们非常困惑,真令人头疼,我也是琢磨了许久,这篇文章就来说下我的想法吧,汉诺塔的背景我就不凑字数了,有兴趣的可以去了解一下,我们直接进入正题,后面还有青蛙跳台阶哦。
1. 汉诺塔
题目描述:
把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。规定:在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
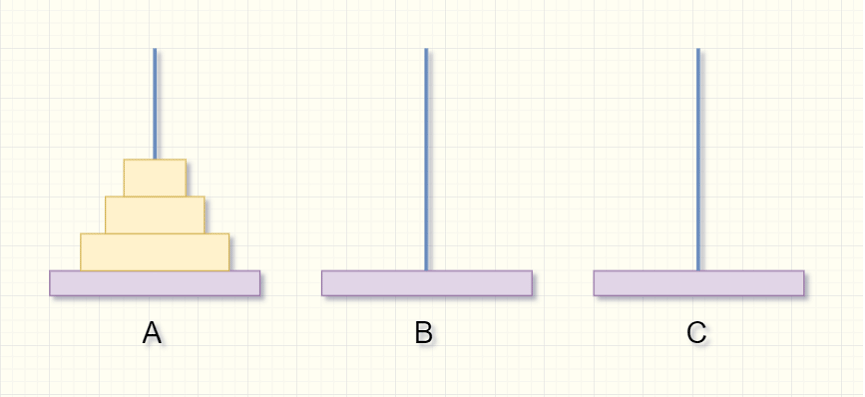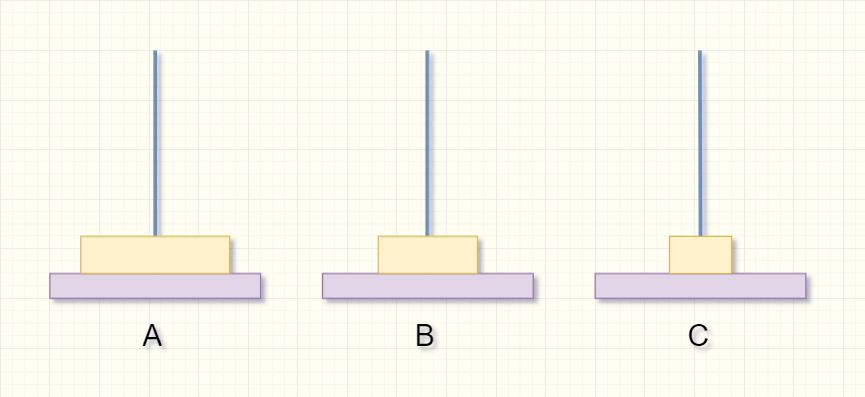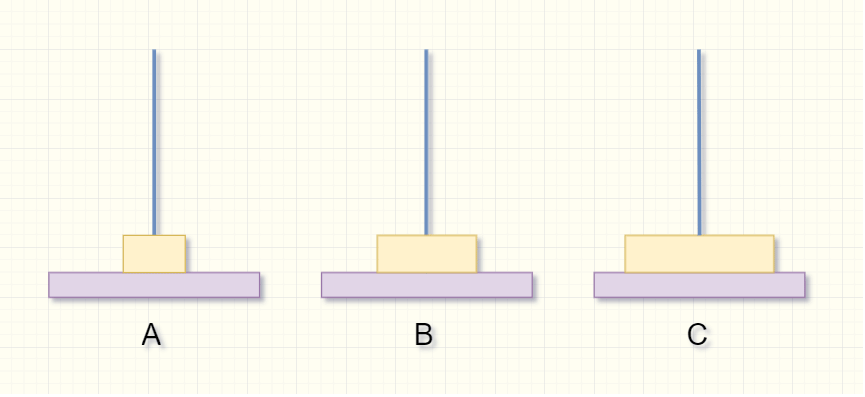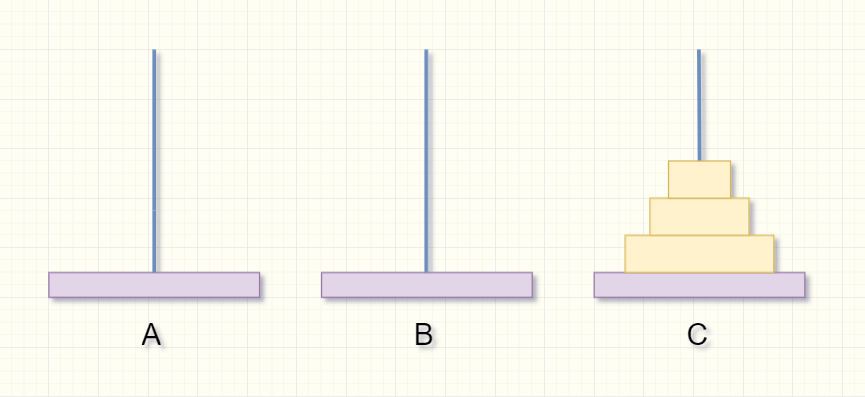
如果要将三个盘从A柱移到第C柱,并且大盘不能在小盘上面该如何做?
- 第一步:先将上面A柱2个盘子通过A柱移动到B柱(如果只有1个盘,就直接将A柱的盘移到C柱),再将最底下的盘子移动到C柱;
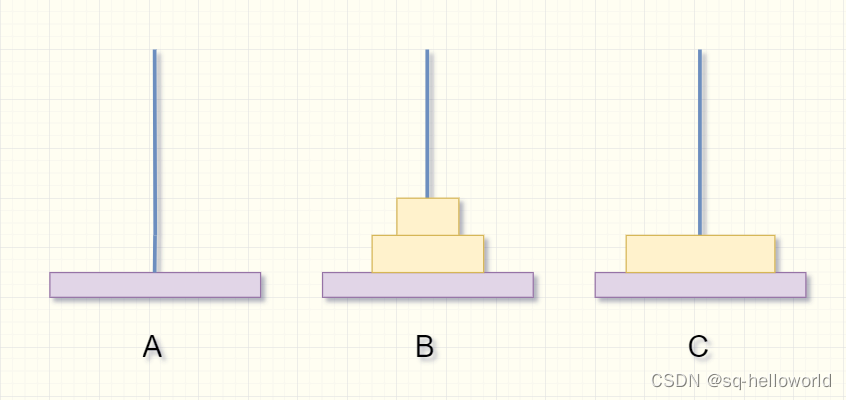
如何把B柱的2个盘移到C柱呢?
- 第二步:同理:将B柱底下的盘不动,将上面的盘通过C柱移动到A柱(如果只有1个盘,就直接将B柱的盘移到C柱),再将最底下的盘子移动到C柱,此时除了已经在C柱上的盘,其他的盘全在A柱上了,那么该情况又回到了第一步,直到最后一个盘移到C柱。
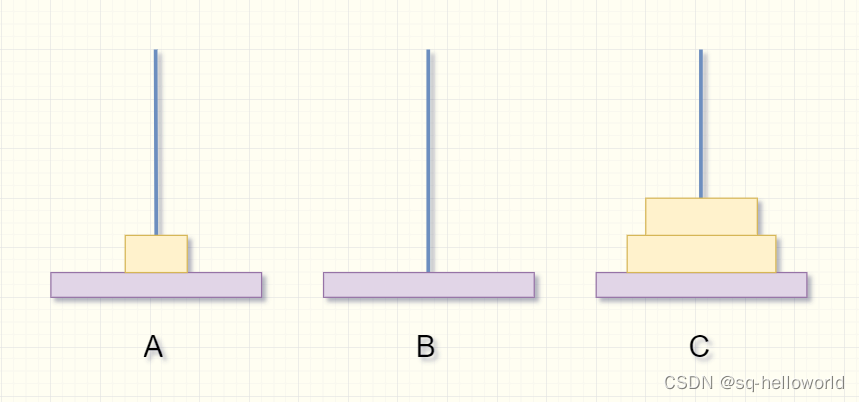
现在就来将思想代码化:
//移动
void move(char pos1 ,char pos2)
{
printf("%c->%c ", pos1, pos2);
}
void hanoi(int n, char pos1, char pos2, char pos3)
{
//只有一个盘时,将pos1移到pos3
//注意:这里的pos不是固定的A,B,C盘,下面会讲
if (n == 1)
{
move(pos1, pos3);
}
else
{
//将n-1个盘通过pos3移到到pos2
hanoi(n - 1, pos1, pos3, pos2);
//移动后将pos1上的最后一个盘移至pos3
move(pos1, pos3);
//将这n-1个盘移至pos3
hanoi(n - 1, pos2, pos1, pos3);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
char A = 'A',B ='B', C = 'C';
hanoi(n,A,B,C);
return 0;
}
递归路径:
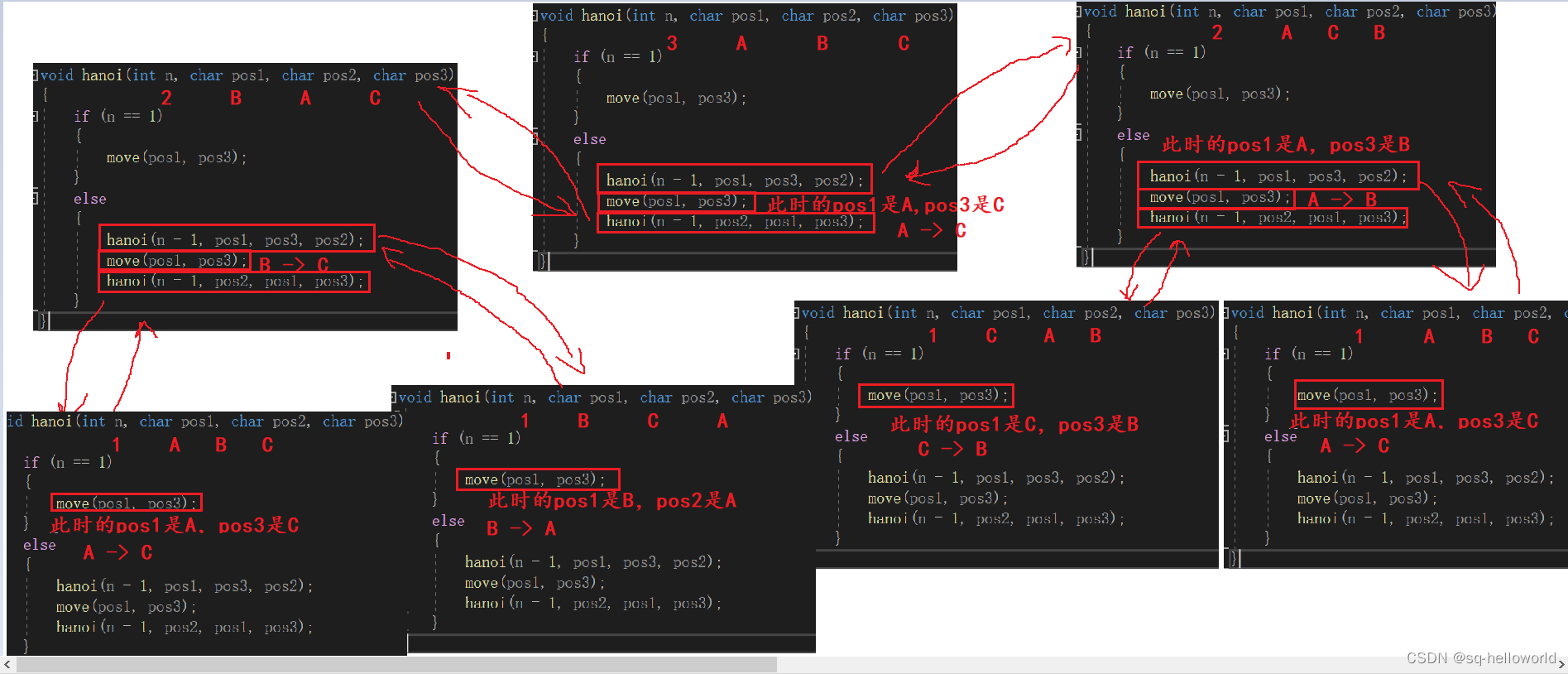
将n-1个移开,再将最后一个盘移至C柱,最后将n- 1个移至C柱,想要将n-1个移开,就要将n-2个移开,再将第n-2个移至C柱,最后将n-2个数移至第n-2上;以此递归,直至n=1,直接移至C柱。
需要注意每次递归都会改变pos1,pos2,pos3,看上图便知。
结果:

2. 青蛙跳台阶
题目描述:
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
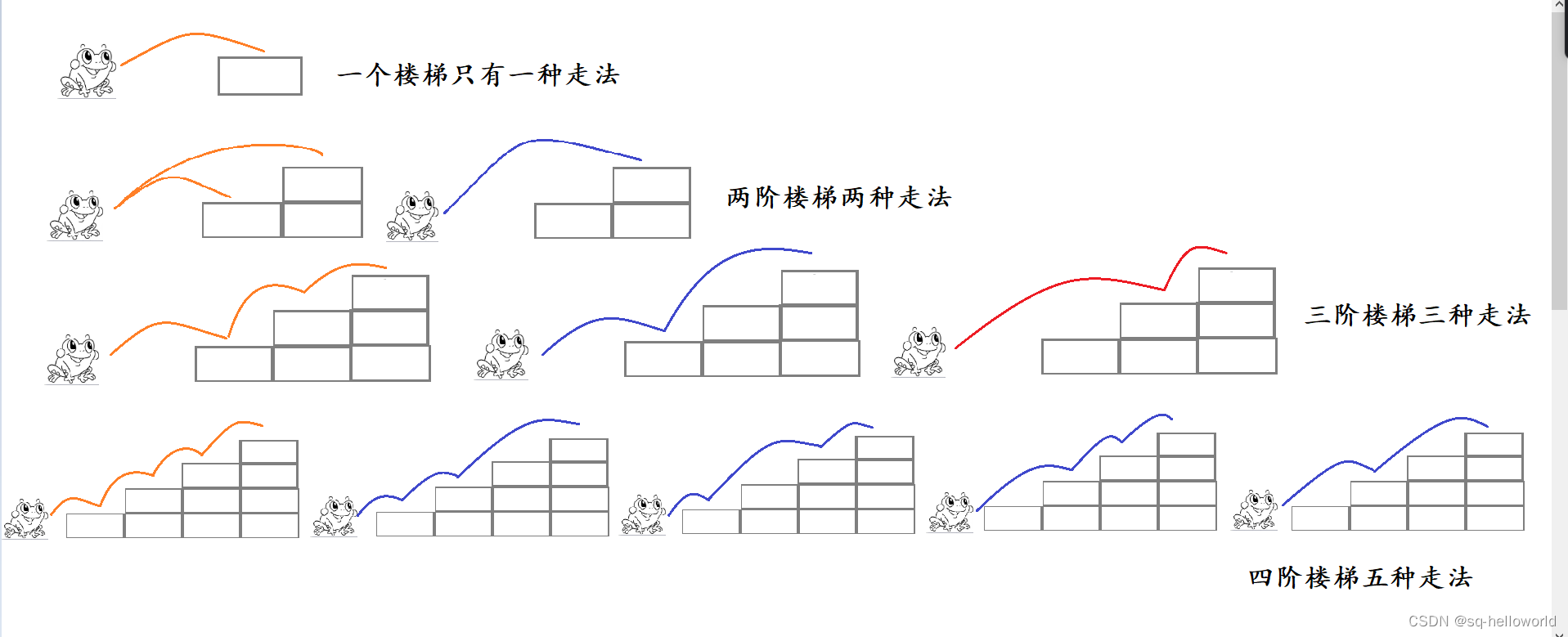
规律总结:
一阶:1种
二阶:2种
三阶:3种
四阶:5种
…
此时我们发现它与Fibonacci数列有着相同的规律1,2,3,5,8,13…,后一个数等于前两个数之和,真正的含义是,当算n阶楼梯走法时,我们先算n-1和n-2阶楼梯的走法,因为,想到n阶会有两种走法,当以一次走一步的走法就会在n-1阶的时候走上来,当以一次走两步的走法,那么就会在n-2走上来,同理,n-1,n-2两者也会有两种走法上来,以此递归到1和2.
int jump_step(int n)
{
if (n == 1)
{
return 1;
}
else if (n == 2)
{
return 2;
}
return jump_step(n - 1) + jump_step(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d", jump_step(n));
return 0;
}
三连支持,感谢!