说起DP,相信点进来的小伙伴们都深受其害
应该很多人和我一样, 导师讲的时候开小差懒得听, 但是课下做题时却一头雾水
所以此篇博客专为想要入门DP的小伙伴们而写,相信大家都能看懂
(如果看懂了就请小伙伴们给我点一个不要钱的赞吧)
(下面有投票)
目录
#概念
#INTRO
#START
#例题
AC
#概念
DP的概念说实话很难懂反正我是懒得看
- 阶段:把所给问题的求解过程恰当地分成若干个相互联系的阶段,以便于求解。过程不同,阶段数可能不同。描述阶段的变量称为阶段变量,常用k表示。阶段的划分一般是根据时间和空间的自然特征来划分,但要便于把问题的过程转化为多阶段决策的过程。
- 状态:状态表示每个阶段开始面临的自然状况或客观条件,它不以人们的主观意志为转移,也称为不可控因素。通常一个阶段有若干状态,状态通常可以用一个或一组数来描述,称为状态变量。
- 决策:表示当过程处于某一阶段的某个状态的时候,可以做出不同的决定,从而确定下一阶段的状态。这种决定称为决策。不同的决策对应着不同的数值,描述决策的变量称决策变量。
- 状态转移方程:动态规划中本阶段的状态往往是上一阶段的状态和上一阶段的决策的结果。由第i段段状态f(i),和决策u(i)来确定第i+1段段状态。状态转移表示为F(i+1)=T(f(i),u(i)),称为状态转移方程。
- 策略:各个阶段决策确定后,整个问题的决策序列就构成了一个决策,对于每个实际问题,可供选择的决策有一定范围,称为允许策略集合。允许策略集合中达到最优效果的策略称为最优策略。
- 必须满足最优化原理和无后效性。
#INTRO
先来看一道题:(熟练掌握递归的可以跳过)
# 数楼梯
## 题目描述
楼梯有 $N$ 阶,上楼可以一步上一阶,也可以一步上二阶。
编一个程序,计算共有多少种不同的走法。
## 输入格式
一个数字,楼梯数。
## 输出格式
输出走的方式总数。
## 样例 #1
### 样例输入 #1
```
4
```
### 样例输出 #1
```
5
```
看过原题的伙伴们可能知道这道题还需要高精, 这里就先不管了
看题我们可以容易地知道:每个楼梯都是由两个或一个楼梯前跳上来的
那么最后一个楼梯(也就是第n个), 就是由n - 1和n - 2上来的
而n - 1是由n - 2和n - 3跳上来的;
同理n - 2是由n - 3 和n - 4跳上来的;
这就是递归;
那么我们就可以写出来以下代码
void step (int now_num) {//主函数中的就是step (n)
if (now_num == 0) {//达到第一个点
ans ++;//算一条路径, 总数加一(记得ans赋值0)
}else if (now_num > 0){
step (now_num - 1);//一个楼梯钱
step (now_num - 2);//两个楼梯前
}
}那么这就是搜索的前身
如果你已经熟练掌握了搜索, 那么我们开始吧
#START
如果给你一个无规律序列, 让你寻找最长上不下降子序列, 你会怎么求呢?
首先想到的肯定是爆搜,枚举每一个子数字, 然后存到数组里, 再比较数组的长度
但是这样真的好吗?时间复杂度真的优吗?
这里就要引出 DP了
用爆搜,会走很多重复的路径

就好比数字4, 搜索1的时候走一遍, 走索2的时候再走一遍,
大大增加了时间复杂度
那么我们能不能把以4为开头的最长不下降子序列的长度存到一个下标为4(数字4在序列中的下标也是4)的数组f里, 然后以后每次遍历到它的时候就不搜索后面的数了,直接加上f[4]?
答案是肯定的,如果你明白了这点,那么恭喜你, 你已经初步明白了DP的思想
明白的伙伴们不禁要问了, 那这不就是记忆化搜索吗?
从莫种程度上来说, 这就是深搜?+ 记忆化
我们继续思考, 一点一点推,?
以3为首的? 最长不下降子序列? 的长度是几呢?
很明显, 长度是1(也就是只有他自己)即f[5] = 1;
那么4呢?
因为4小于3, 所以3, 4 不能构成? 不下降子序列? , 那么同理
以4为首的? 最长不下降子序列? 的长度也是1 (同样只有他本身)即f[4] = 1
对于2 可以观察到 2, 4 和2, 3都构成? 不下降子序列? , 而且长度都是2;
很明显f[3] = 2;
继续看5, 没有 所以f[2] = 1;
最最后看数字1,:?1,2和1,3和1,4和1,2,4和1,2,3都是不下降子序列, 那么我们找到其中最长的;
就是f[1] = 3;
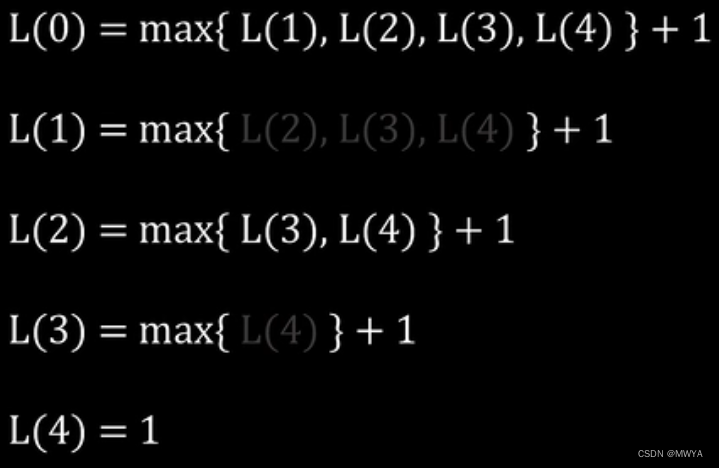
注:图片是从0开始的(不要懵了)?
最后我们一个打擂, 找到最长不下降子序列的长度是3;
简单是不是?
贴一下主代码:
f[n] = 1;//最后一个数的最长不下降子序列长度就是1, 要赋值
for (int i = n - 1; i >= 1; i --) {//刚刚已经赋值过了就直接从n - 1开始
maxn = 0;//这里要重新赋值
for (int j = 1; j < n; j ++)
if (a[j] >= a[i] && f[j] > maxn) //两个条件
maxn = f[j];
f[i] = maxn + 1;//还要算上它本身
}
maxn = -1;//打擂
for (int i = 1; i <= n; i ++) {
maxn = max (maxn, f[i]);
}
//那么最后maxn就是最长不下降子序列的长度了那如果现在他题目说让输出最长子序列呢?
?你会怎么做呢?
我们先把题目贴出来:
我实在没有在洛谷里找到这道题
【题目描述】
设有由n(1≤n≤200)个不相同的整数组成的数列,记为:b(1)、b(2)、……、b(n)若存在i1<i2<i3<…<ie 且有b(i1)<=b(i2)<=…<=b(ie)则称为长度为e的不下降序列。程序要求,当原数列出之后,求出最长的不下降序列。
例如13,7,9,16,38,24,37,18,44,19,21,22,63,15。例中13,16,18,19,21,22,63就是一个长度为7的不下降序列,同时也有7 ,9,16,18,19,21,22,63组成的长度为8的不下降序列。
【输入】
第一行为n,第二行为用空格隔开的n个整数。
【输出】
第一行为输出最大个数max(形式见样例);
第二行为max个整数形成的不下降序列,答案可能不唯一,输出一种就可以了,本题进行特殊评测。
【输入样例】
14
13 7 9 16 38 24 37 18 44 19 21 22 63 15
【输出样例】
max=8
7 9 16 18 19 21 22 63有点难搞哦
仔细想一想
如果我们再定义一个数组, 以p[i]为例
存储的是以p[i]为首的最长不下降子序列的第二个数的下标
这里再放一下图
![]()
以18为例, 以它开头的最长不下降子序列分别为18,19,21,22,63;
第二个数19的下表为10
那么p[8] = 10;
同理p[10] = 11;
p[11] = 12;
p[12] = 13;
那就太简单了
?中和上面所说的数组f, 我们就可以得到下面这个表格:

?简单实在是太简单了 (讲这么详细了, 麻烦点一个不花钱的赞吧)
直接贴代码
#include <iostream>
using namespace std;
const int N = 10050;
int n;
int a[N], f[N], p[N];
int maxn;
int main () {
cin >> n;
f[n] = 1;//这里省略了p[n] = 0因为定义的是全局变量
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = n; i >= 1; i --) {
int cmp = 0;
maxn = 0;
for (int j = i + 1; j <= n; j ++) {
if (a[j] >= a[i] && f[j] > maxn) {
maxn = f[j];
cmp = j;//存下标
}
}
f[i] = maxn + 1;
p[i] = cmp;//第二个数的下标
}
maxn = -1;
int cnt;
for (int i = 1; i <= n; i ++) {
if (f[i] > maxn) {
maxn = f[i];
cnt = i;
}
}
cout << "max=" << maxn << endl;
int s = cnt;
while (s) {//最后一个数是0(上面说了)
cout << a[s] << " ";
s = p[s];//直接让s等于最长子序列的下一个数
}
return 0;
}提交一下, 就AC了!!!
#例题
下面我们再来看一道例题
(这里就以洛谷为例了)
# [NOIP2004 提高组] 合唱队形
## 题目描述
$n$ 位同学站成一排,音乐老师要请其中的 $n-k$ 位同学出列,使得剩下的 $k$ 位同学排成合唱队形。
合唱队形是指这样的一种队形:设 $k$ 位同学从左到右依次编号为 $1,2,$ … $,k$,他们的身高分别为 $t_1,t_2,$ … $,t_k$,则他们的身高满足 $t_1< \cdots <t_i>t_{i+1}>$ … $>t_k(1\le i\le k)$。
你的任务是,已知所有 $n$ 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
## 输入格式
共二行。
第一行是一个整数 $n$($2\le n\le100$),表示同学的总数。
第二行有 $n$ 个整数,用空格分隔,第 $i$ 个整数 $t_i$($130\le t_i\le230$)是第 $i$ 位同学的身高(厘米)。
## 输出格式
一个整数,最少需要几位同学出列。
## 样例 #1
### 样例输入 #1
```
8
186 186 150 200 160 130 197 220
```
### 样例输出 #1
```
4
```
## 提示
对于 $50\%$ 的数据,保证有 $n \le 20$。
对于全部的数据,保证有 $n \le 100$。提高组, 好家伙真水
分析一下:
我们只要找的合唱的最长队形k
再用n - k就得到答案了
至于k,我们只要将每一个数i从1~i的最长上升子序列长度?加上?i~n的最长下降子序列长度就行了
就很简单
贴代码:
#include <iostream>
using namespace std;
const int N = 10050;
int n;
int a[N], f1[N], f2[N], s[N];
int maxn;
int main () {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
f1[n] = 1;
f2[1] = 1;
for (int i = n - 1; i >= 1; i --) {//1 ~ i
maxn = 0;
for (int j = i + 1; j <= n; j ++)
if (a[j] < a[i] && f1[j] > maxn)
maxn = f1[j];
f1[i] = maxn + 1;
}
for (int i = 2; i <= n; i ++) {// i ~ n
maxn = 0;
for (int j = 1; j <= i - 1; j ++)
if (a[j] < a[i] && f2[j] > maxn)
maxn = f2[j];
f2[i] = maxn + 1;
}
maxn = -1;
for (int i = 1; i <= n; i ++) maxn = max (maxn, f1[i] + f2[i] - 1);
cout << n - maxn;
return 0;
}然后就AC了
很棒对不对?
恭喜你已经掌握了DP的初步思想(没话编了再说一遍)
既然都看到这里了(我也写了这么长时间了)就请你点个免费的赞吧
这不仅是对我无限的鼓励, 更是你良好品德的外在表现
谢了