目录
五、编写代码实现,模拟用户登录情景,并且只能登录三次。(只允许输入三次密码,如果密码正确则提示登录成功,如果三次均输入错误,则退出程序。)
一、计算n的阶乘
1.一般解法
这道题目比较简单,下面就是我们的代码实现
#include<stdio.h>
int main()
{
int i, ret = 1;
int n;
scanf("%d", &n);
for (i = 1; i <=n; i++)
{
ret = ret * i;
}
printf("%d", ret);
}但是我们说这还不够。因为如果我们输入的数据比较大,就很可能会发生溢出,因为int类型最多有32个比特位,也就是最大能表示2的三十二次方的大小,那么如何表达更大类型的数呢,答案是将int改为double,这样最大就可以表示2的64次方的大小了。
2.优化不能表示出较大数的阶乘
#include<stdio.h>
int main()
{
int i;
double ret = 1;
int n;
scanf("%d", &n);
for (i = 1; i <=n; i++)
{
ret = ret * i;
}
printf("%.0f", ret);
}二、 计算 1!+2!+3!+……+10!
1.循环嵌套解法
这道题是第一题的一个拓展。既然我们已经有了第一道题的基础,这第二道题相信大家也应该有思路,那便是循环嵌套一层。下面是代码实现
#include<stdio.h>
int main()
{
int i, j;
int ret = 1;
int sum = 0;
for (i = 1; i <= 10; i++)
{
ret = 1;
for (j = 1; j <= i; j++)
{
ret = ret * j;
}
sum = sum + ret;
}
printf("%d", sum);
return 0;
}这样确实是实现了我们的代码,但是我们说这还不够好,因为效率太低,试想一下,如果这个数很大呢,让加到100,1000呢,那这些阶乘运算中出现了大量的重复性计算,使得我们的计算出答案所需的时间增加,所以为了优化,我们可以只需使用一次for循环就可以得出答案。
?2.一次循环解法(优化计算时间)
#include<stdio.h>
int main()
{
int i;
int ret = 1;
int sum = 0;
for (i = 1; i <= 3; i++)
{
ret = ret * i;
sum = sum + ret;
}
printf("%d", sum);
return 0;
}这样的话,我们的时间复杂度也大大降低。时间复杂度的概念将在以后的文章中详细讲到。这里读者暂时不用深究。
三、在一个有序数组中查找具体的某个数字n
1.遍历查找
比如说我们在一个从1--10的数组中找出7,最简单的方法当然是遍历了,代码实现如下
#include<stdio.h>
int main()
{
int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };
int k = 7;//要找它
int i;
int flag = 0;
for (i = 0; i < 10; i++)
{
if (arr[i] == k)
{
printf("找到了,下标是%d",i);
flag = 1;
break;
}
}
if (flag == 0)
{
printf("找不到");
}
return 0;
}但是,这效率太低了,因为我们最坏要找n次,n为数组的个数。那么有没有什么更高效的方法呢?我们说,是有的,接下来给大家介绍一个二分查找算法,也叫折半查找算法。
2.二分查找算法(优化了查找时间)
如下图所示,这是一个数组,如果我们想找到7这个元素,如何找呢?

?首先我们先确定左下标和右下标,方便我们知道查找到了那个位置,此时我们所查找的范围为[left,right]这个闭区间,如下图所示
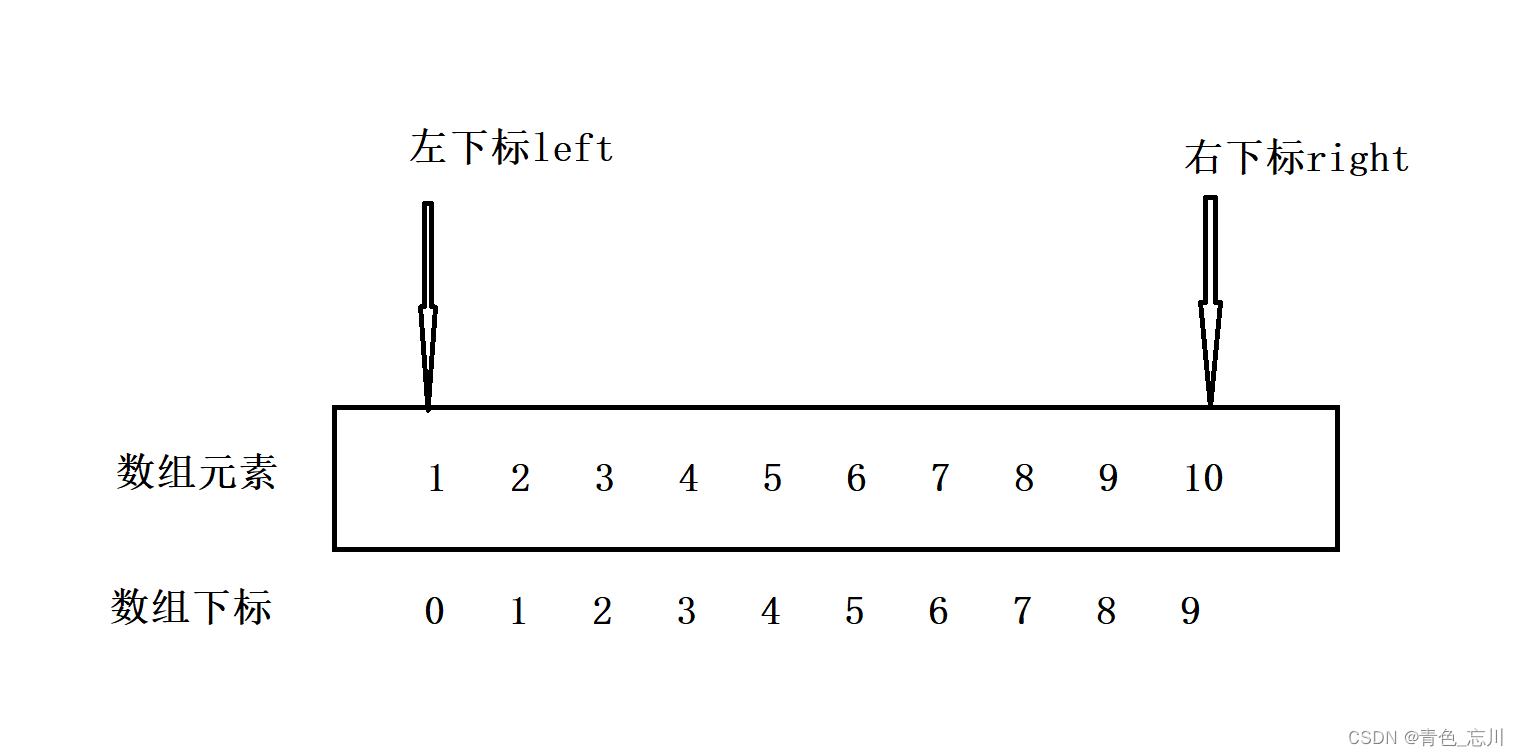
?紧接着,我们引入一个中间量mid作为一个下标,mid这个数组下标为左下标与右下标之和除以2,取出商的部分,忽略掉余数。即mid=(left+right)/2,如下图所示,为第一次二分。
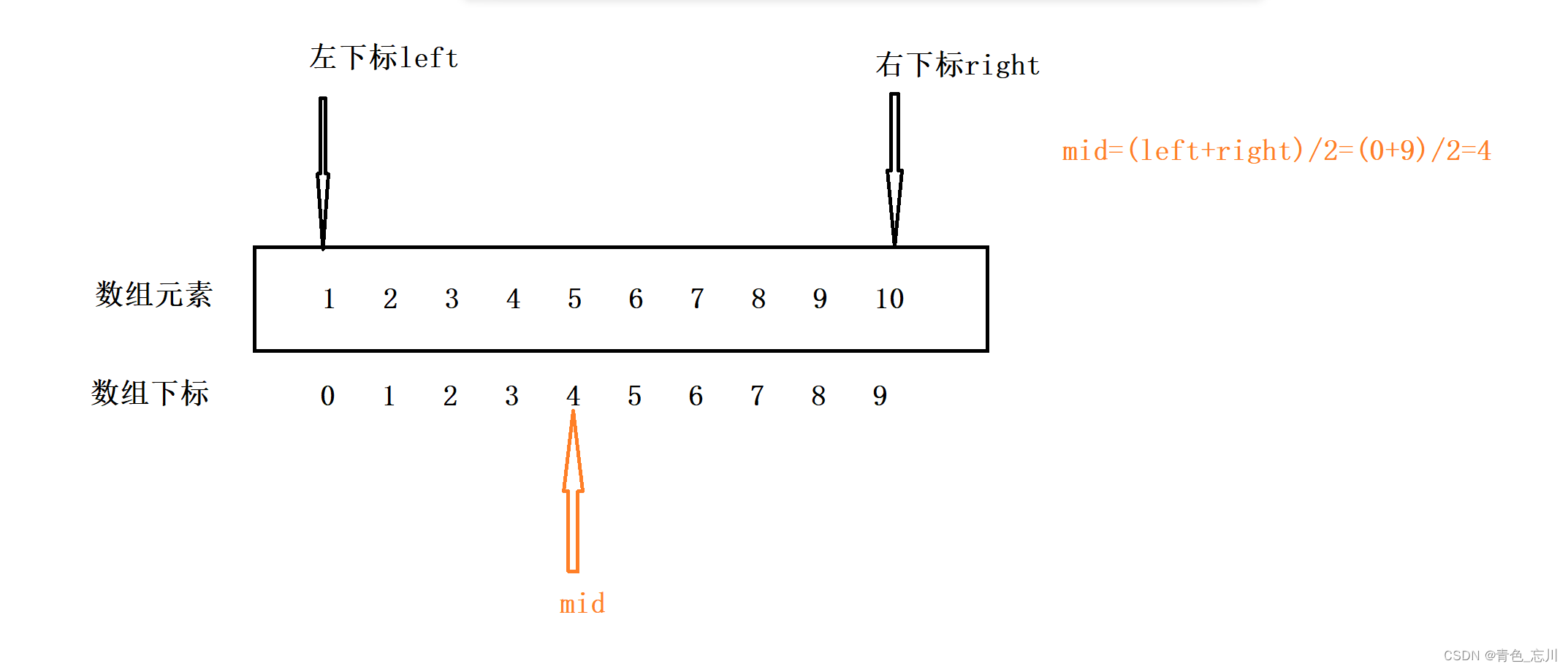
?查找之后我们发现,arr[mid]<7,也就是说,7在arr[mid]的右侧,所以此时[left,mid]这个闭区间就不在我们的查找范围内了,我们新的查找范围为(mid,right]这个左开右闭区间,为了和前面统一,都为闭区间,我们不妨令新的区间为[mid+1,right]这个闭区间。在这个闭区间上,我们令left=mid+1,这样我们要查找的闭区间为[left,right]了,这样一来,我们就会发现,这好像可以用一个循环,通过一个循环,让它来一直执行下去,我们就能很高效的找出所需要查找的闭区间了。但是,为了大家更好的理解,我们继续画图往下执行。
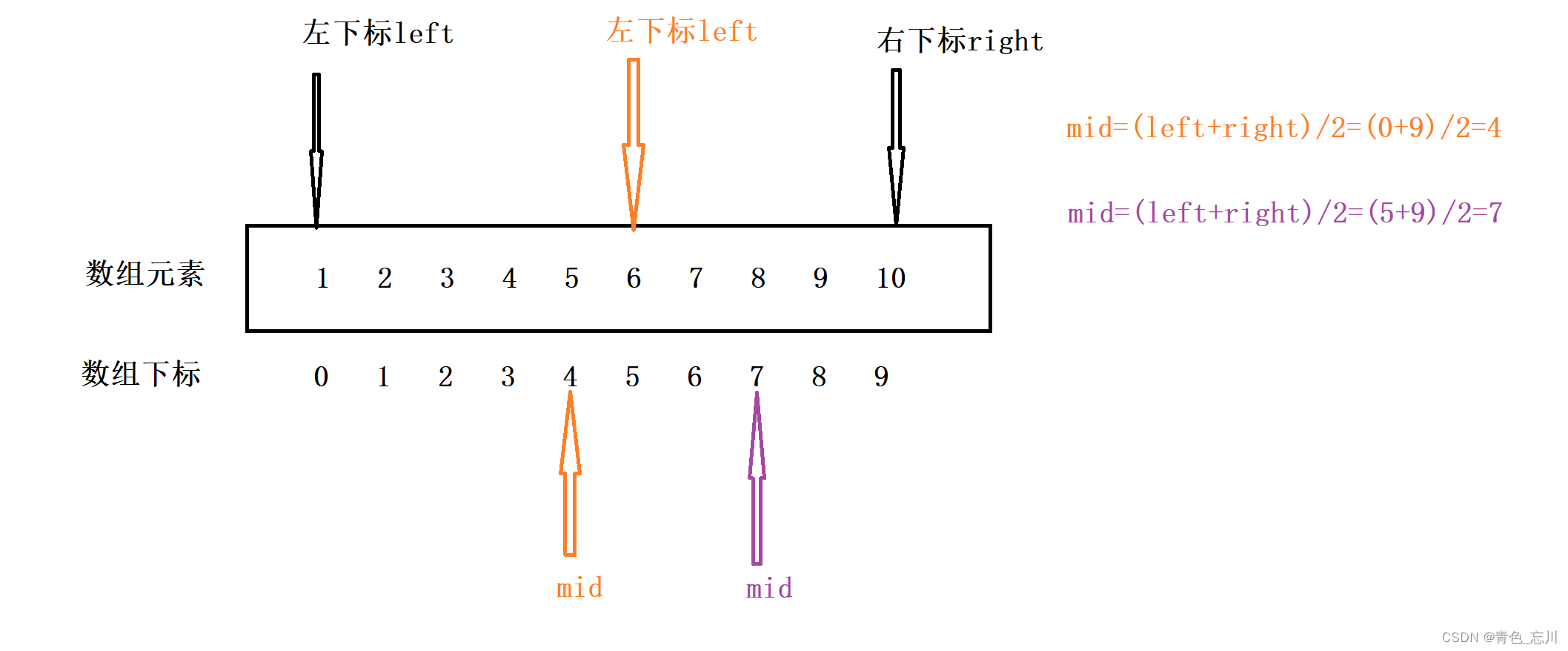
上图中,这是我们第二次找出中间值的图解,为图中紫颜色部分,我们发现arr[mid]>7,那说明[mid,right]这个闭区间中没有7,于是我们所需要查找的新区间为[left,mid-1]这个闭区间。我们同样令right=mid-1,这样我们的新的需要查找的区间为[left,right]了
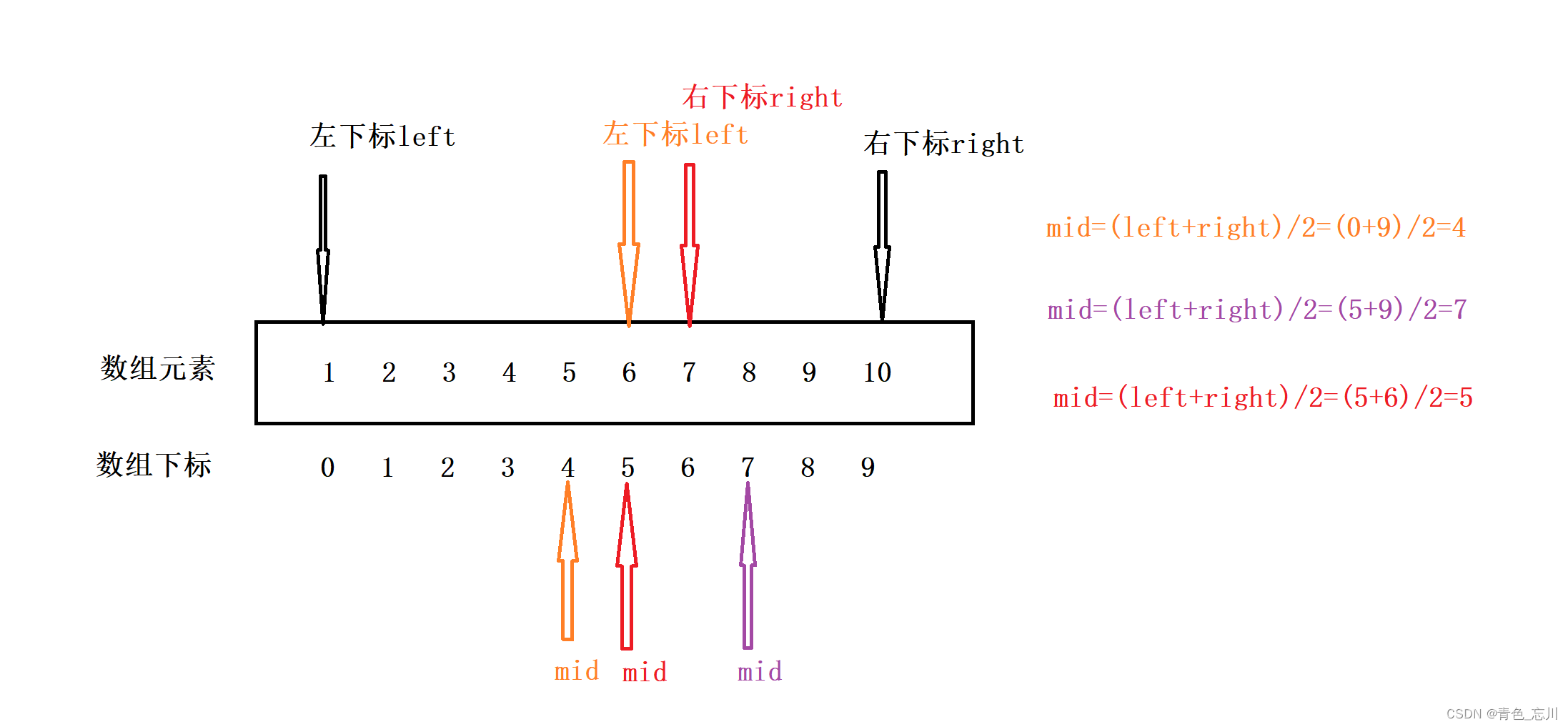
?如上图所示,红色部分为新下标示意图,由于arr[mid]<7,所以根据上面的原理可得,[left+1,right]为新区间。我们继续进行查找。
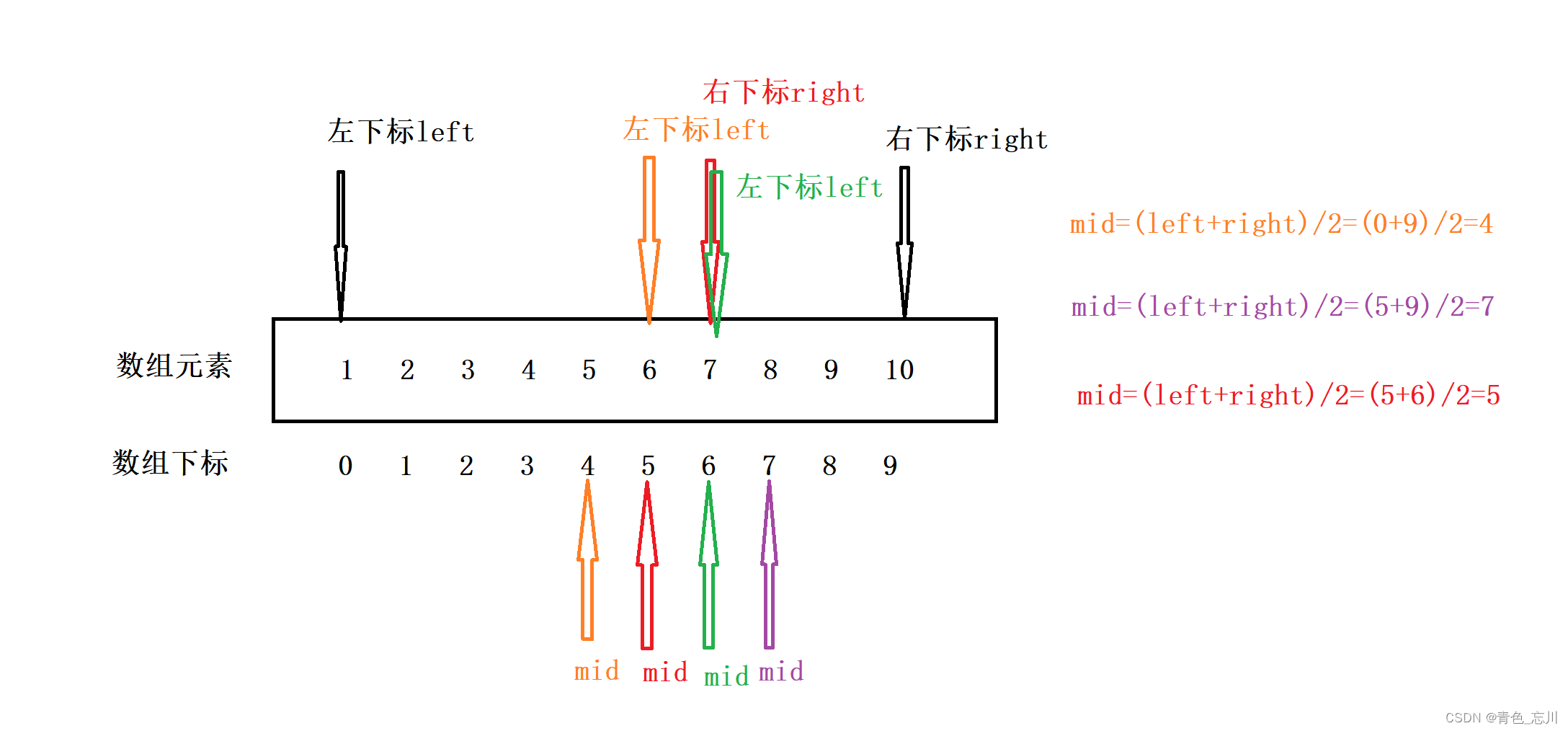
?如上图所示,此时我们的arr[mid]=7,也就是说找到了,我们就可以返回这个mid,就是我们所找到的下标。
以上就是我们二分查找算法的图解,相信大家都已经看懂了吧,有人说,那么既然这是个循环实现的,那么循环里面的条件应该填什么呢?其实很简单,我们根据上面的图解也能发现,只有left<=right时,也就是说,左下标小于等于右下标时候,因为不可能右下标小于左下标,这样我们的程序才能执行下去,这也就是我们的判断条件。
那么我们将上面的代码实现以下吧
#include<stdio.h>
int main()
{
int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };
int k = 7;//要找它
int left = 0;
int right = 9;
int flag = 0;
int mid = 0;
while (left <= right)
{
mid = (left + right) / 2;
if (arr[mid] > k)
{
right = right - 1;
}
else if (arr[mid] < k)
{
left = left + 1;
}
else
{
printf("找到了,下标为%d", mid);
flag = 1;
break;
}
}
if (flag == 0)
{
printf("找不到");
}
return 0;
}四、编写代码,演示多个字符从两端移动,向中间汇聚。
1.一般解法
我们先直接给出代码
#include<stdio.h>
#include<string.h>
int main()
{
char arr1[] = "welcome to world";
char arr2[] = "****************";
int left = 0;
int right = strlen(arr2) - 1;
while (left <= right)
{
arr2[left] = arr1[left];
arr2[right] = arr1[right];
printf("%s\n", arr2);
left++;
right--;
}
return 0;
}在这个代码中,我们给出两个字符数组并且进行初始化,arr1是需要被慢慢显现出来的,arr2是需要被打印出来的,以此来展示出效果,我们采用和二分查找类似的思想,使用一个左下标,和一个右下标。我们右下标是直接采用一个库函数strlen计算出来的,因为计算出来的是长度,所以我们需要减1,来代表下标。然后我们逐步将arr1的数组赋值给arr2,并且打印出arr2。然后一直循环,循环条件也与二分查找类似,只需要我的左下标小于等于右下标,我就可以继续执行下去
运行截图为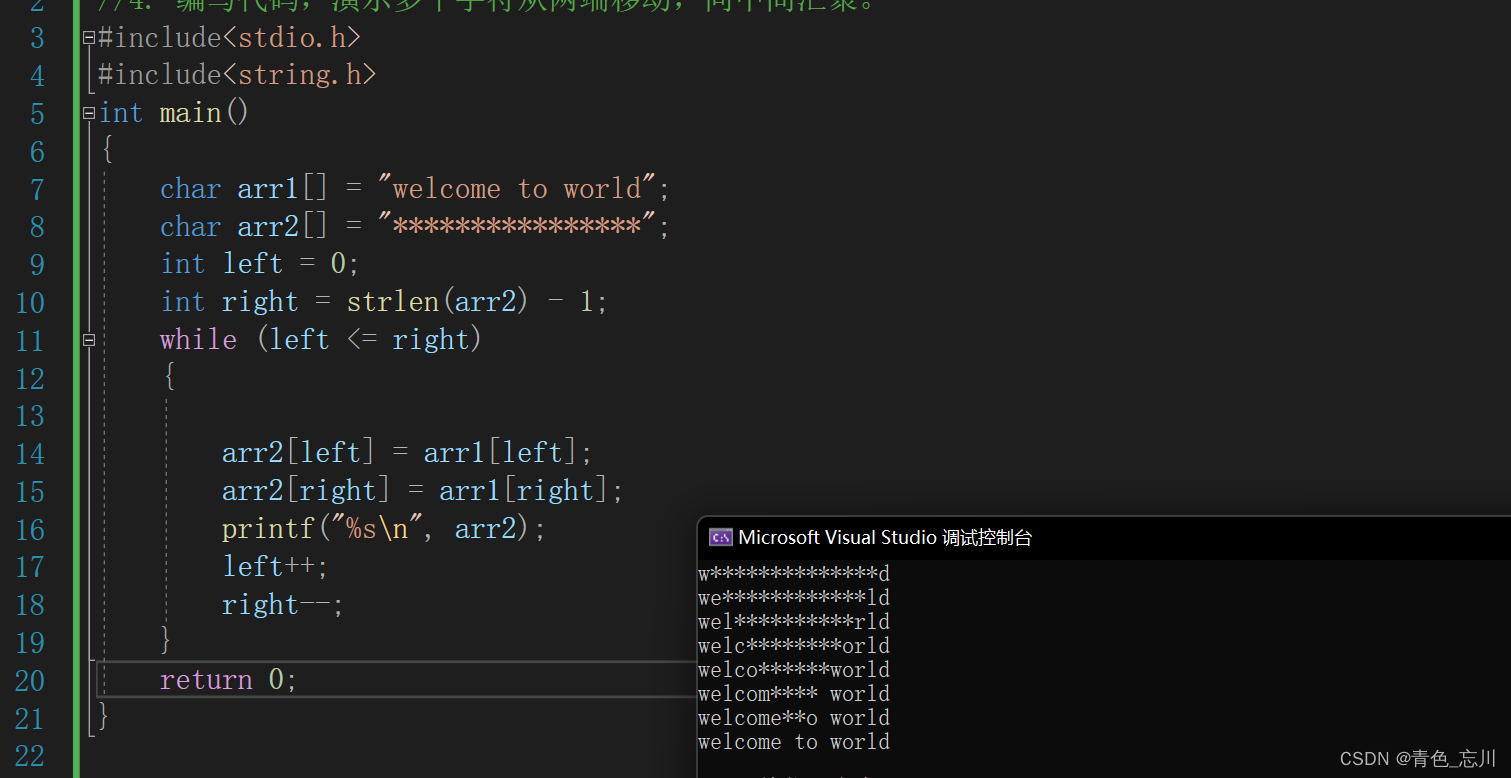
?但是我们可不可以对它在优化一点呢。比如说我们想要在加上两个需求,一个需求是使得它打印以此,停顿一秒钟,然后继续打印。另外一个需求是,打印一次,清屏一次呢?我们说,是可以的。在这里我们就需要使用到两个库函数了。
2.优化后的解法(提高用户体验感)
Sleep()//作用是休眠,单位是毫秒??? 需要调用头文件include<window.h>
system("cls") //作用是清屏,需要调用头文件include<stdlib.h>
?以下就是我们最终的代码了。读者可以自行去运行
#include<stdio.h>
#include<string.h>
#include<windows.h>
#include<stdlib.h>
int main()
{
char arr1[] = "welcome to world";
char arr2[] = "****************";
int left = 0;
int right = strlen(arr2) - 1;
while (left <= right)
{
arr2[left] = arr1[left];
arr2[right] = arr1[right];
printf("%s\n", arr2);
left++;
right--;
Sleep(1000);
system("cls");
}
printf("%s\n", arr2);
return 0;
}
五、编写代码实现,模拟用户登录情景,并且只能登录三次。(只允许输入三次密码,如果密码正确则提示登录成功,如果三次均输入错误,则退出程序。)
1.一个经典的错误,标准的零分
我们先给出一段代码,并且尝试分析一下,判断是否正确?
#include<stdio.h>
int main()
{
int i;
int flag = 0;
char password[20] = {0};
for (i = 0; i < 3; i++)
{
printf("请输入密码:");
scanf("%s", password);
if (password == "123456")
{
printf("密码正确\n");
flag = 1;
break;
}
else
{
printf("密码第%d次输入错误\n", i + 1);
}
}
if (flag == 0)
{
printf("密码三次输入错误,退出程序");
}
return 0;
}当我们想要输入一个密码时候,我们首先得定义一个字符数组来存放密码。接着我们使用一个循环,用来记录三次密码的上限,在循环中,我们输入密码,然后使用一个if语句来判断,我们直接使用一个==来进行判断,然后如果对,就跳出循环,不对,则继续循环。这个逻辑似乎听着没问题,但是事实真的是这样吗?我们运行一下试试
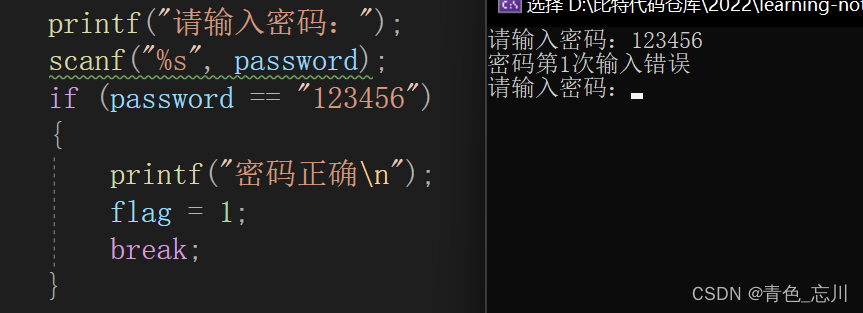
我输入了123456,居然提示我密码错误?怎么回事?哪里出问题了?其实这里犯了一个经典的错误,标准的零分。我们说,判断两个字符串相等不是这样判断的,这样判断就是经典的错误标准的零分。
那我们应该怎么判断呢?,其实c语言中提供了一个库函数,叫做strcmp(? ,),这个库函数用于比较字符串。
那么如何比较呢?是这样比较的
//判断两个字符串是否相等,不能直接使用==
int ret = strcmp(password,"123456");
//如果两个字符串相等,则返回0
//如果password小于"123456",也就是第一个字符串小于第二个字符串,则返回小于0的一个数字
//如果password大于"123456",也即是第一个字符串大于第二个字符串,则返回大于0的一个数字有的人可能有疑惑了,两个字符串咋比较的?是比较他们的长度吗?我们说不是的,字符串的比较是一个一个往下比较的,也就是说,第一个字符串的第一个字符与第二个字符串的第一个字符进行比较,比较的是他们的ASCII值,如果第一位能比较出来谁大,则就是哪个字符串大,如果第一位都相等,则判断两个字符串的第二位,如此循环下去进行判断,直到遇到\0。也就代表着字符串的结束。关于字符串的一些库函数,我们在后面还会更加详细的讲解,读者暂时只需要了解到,我目前所讲解到的即可,注意使用这个库函数需要引用头文件<string.h>
所以最终的代码实现为,
#include<stdio.h>
#include<string.h>
int main()
{
int i;
int flag = 0;
char password[20] = {0};
for (i = 0; i < 3; i++)
{
printf("请输入密码:");
scanf("%s", password);
if (0 == strcmp(password, "123456"))
{
printf("密码正确\n");
flag = 1;
break;
}
else
{
printf("密码第%d次输入错误\n", i + 1);
}
}
if (flag == 0)
{
printf("密码三次输入错误,退出程序");
}
return 0;
}六、求最大公约数
1.一般解法
缺点:计算量太过于复杂。
#include<stdio.h>
int main()
{
int m = 24;
int n = 18;
int max = m > n ? m : n;
while (max>0)
{
if (m % max == 0 && n % max == 0)
{
printf("%d", max);
break;
}
max--;
}
return 0;
}
2.辗转相除法
这种方法不需要掌握原理,因为涉及到数学方面的知识
我们的想法是这样的,m和n这两个数,用m对n取模,并记录结果t,如果结果不为0,则把n给m,t给n,如此循环下去。知道结果为0,最终答案为n
#include<stdio.h>
int main()
{
int m = 24;
int n = 18;
int ret;
while (m % n != 0)
{
ret = m % n;
m = n;
n = ret;
}
printf("%d", n);
return 0;
}