[C++知识库]C. Orac and LCM(gcd与lcm的性质)

Problem - 1350C - Codeforces

?题意:

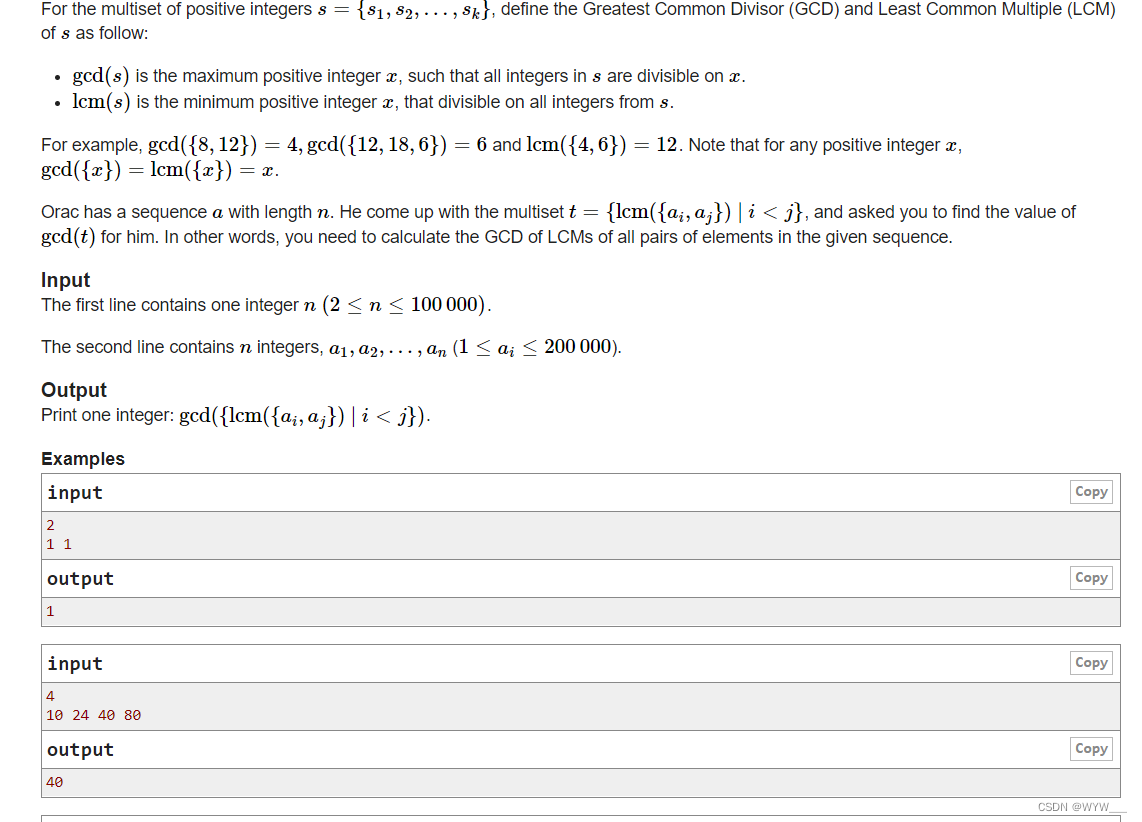
对于正整数的多集合s={s1,s2,...,sk}，定义s的最大公除数（GCD）和最小公倍数（LCM）如下。

gcd(s)是最大的正整数x，使得s中的所有整数都能在x上被除。
lcm(s)是最小的正整数x，它能被s中的所有整数整除。
例如，gcd({8,12})=4,gcd({12,18,6})=6和lcm({4,6})=12。注意，对于任何正整数x，gcd({x})=lcm({x})=x。

Orac有一个长度为n的序列，他想出了一个多集t={lcm({ai,aj}) | i<j}，并要求你为他找到gcd(t)的值。换句话说，你需要计算给定序列中所有元素对的LCM的GCD。

输入
第一行包含一个整数n（2≤n≤100000）。

第二行包含n个整数，a1,a2,...,an (1≤ai≤200000)。

输出
打印一个整数：gcd({lcm({ai,aj}) | i<j})。

题解:

对于a1产生的lcm有lcm(a1,a2),lcm(a1,a3) ... lcm(a1,an)

对于他们的gcd1 = gcd(lcm(a1,a2),lcm(a1,a3) ... lcm(a1,an))

他们都有公因数a1所以可以写成

gcd1 = (a1,gcd(a2,a3,...an))

同理其他ai也可以写成上面形式

答案可以表示为gcd(gcd1,gcd2...gcdn)

#include<iostream>
#include<algorithm>
#include<map>
#include<string>
using namespace std;
long long a[200050],gcd[200050];

int main()
{
	int n;
	cin >> n;
	for(int i = 1;i <= n;i++)
	{
		cin >> a[i];
	}
	for(int i = n;i >= 1;i--)
	{
		gcd[i] = __gcd(gcd[i+1],a[i]);
	}
	long long ans = 0;
	for(int i = 1;i <= n;i++)
	{
		ans =__gcd(ans,a[i]*gcd[i+1]/(__gcd(a[i],gcd[i+1])));
	}
	cout<<ans;

}