1.根据二叉树创建字符串?

链接：根据二叉树创建字符串：力扣

??

?

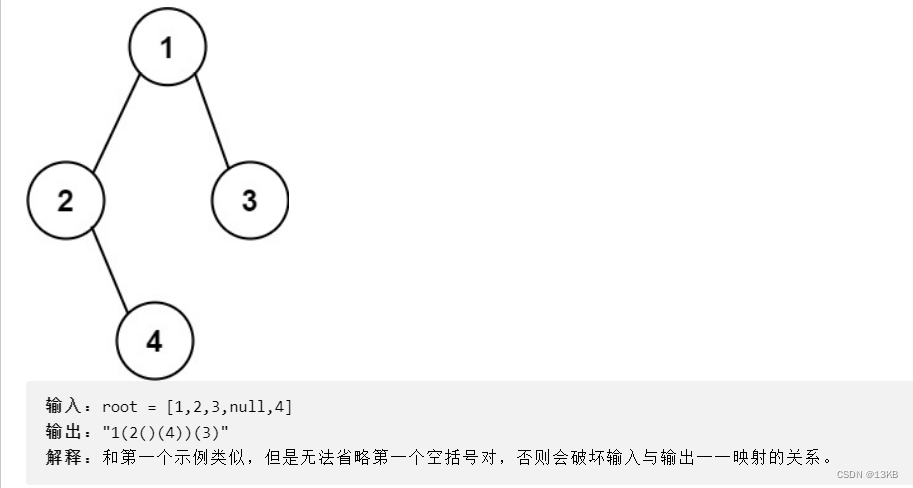
解析：题目是按照前序遍历根，左子树，右子树的遍历方式来存储节点值的。

1(左)(右)?->1((左)(右))((左)(右))。第一种情况不说了，看第二种情况，2的左子树为空，又又子数，但是他的左子树的括号不能省略，你要是省略了就不知道这个4是他的左子树还是右子树。
class Solution {
public:
    string tree2str(TreeNode* root) {
         if(root==nullptr)
            return string();
            //空树就返回一个空的string对象就可以了
            string str;
            str+=to_string(root->val); //根

            str+="(";              //左子树
            str+=tree2str(root->left);
            str+=")";
  
            str+="(";                //右子树
            str+=tree2str(root->right);
            str+=")";
            
            return str;
    }
};
to_string函数是专门让将数字常量转换为字符串，返回值为转换完毕的字符串。

但是这个还不算完，因为这样我们把所有的括号都打印了，该省去的都打印出来了。

啥时候省略？

对于左子树来说，左空右空省括号，左空右有(右子树还有数值）不能省，所以只要右子树是空就一定省去括号。
class Solution {
public:
    string tree2str(TreeNode* root) {
         if(root==nullptr)
            return string();
            
            string str;
            str+=to_string(root->val);
            if(root->left||root->right)
            {
                str+="(";
            str+=tree2str(root->left);
            str+=")";
            }
            if(root->right)
            {
                 str+="(";
            str+=tree2str(root->right);
            str+=")";
            }

            return str;
    }
};

?2.二叉树分层遍历

二叉树的分层遍历1：力扣?

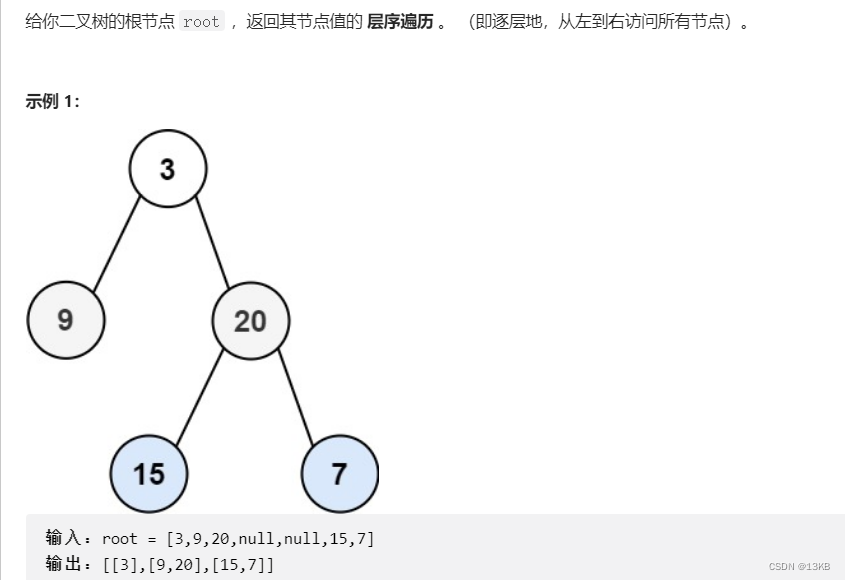
其实这个用队列解决特别爽，先放根进去，然后放左右子树进去，再把根取出队列，再放进去第三代，然后取出第二代。

但是这个有一个疑问，就比如我们取出根后第二三代都在队列中，咋判断这些数是第二代的还是第三代的？

这里我们用levelSize来记录每一代的个数，那这样即使隔代也能正确出队列了。
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q;   //创建一个队列
        size_t levelSize=0;   //记录每一层的实节点个数
       if(root)  //根不为空，进队列
       {
           q.push(root);
           levelSize=1;  // 记录第一代的个数
       }
       vector<vector<int>> vv;
       while(!q.empty())
       {
           vector<int> v;
           for(int i=0;i<levelSize;i++)
           {
               TreeNode* front=q.front();
               q.pop();
               v.push_back(front->val);

               if(front->left)
               {
                   q.push(front->left);
               }
               if(front->right)
               {
                   q.push(front->right);
               }
           }
           vv.push_back(v);
               levelSize=q.size();
       }
           return vv;
       
    }
};
vv：创造的一个二维数组，用来存放二叉树的数据的，他的每一行就是每一代。
v:? 一维数组，在这个循环里是用来存放每一代的数据的。
front:用来保存每一个出队列后的数值。
当把每一行都给vv之后，改变levelSize使他记录的是下一代的个数。

3.最近公共祖先?

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先：力扣?

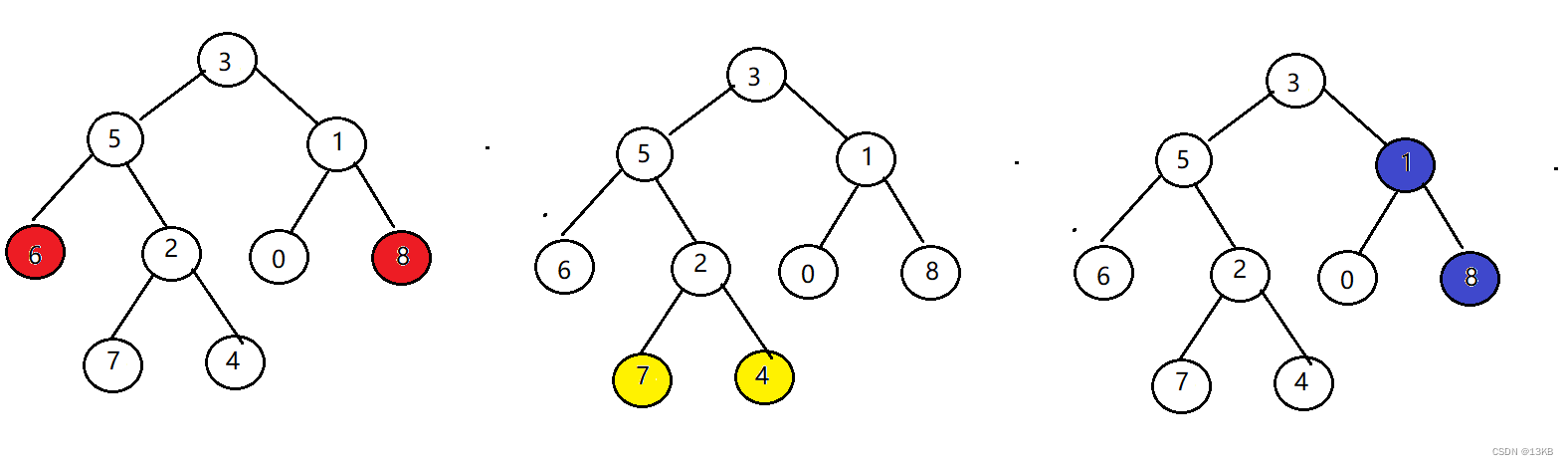
?这个题会遇到这三种情况;

p,q分别在根的两边；都在左边；都在右边。

class Solution {
    bool Find(TreeNode* sub, TreeNode* x)  //查找p,q到底在哪一边
    {
        if(sub==nullptr)
        {
            return false;
        }
        if(sub==x)  //找到了
        {
            return true;
        }
        return Find(sub->left,x)||Find(sub->right, x);
    }
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
       if (root==nullptr)
       {
           return nullptr;
       }
       if(root==p||root==q)
       {
           return root;
       }
       bool pleft,pright,qleft,qright;  
       //分别判断p,q到底在哪一边
        pleft=Find(root->left, p);
        pright=!pleft;
        qleft=Find(root->left,q);
        qright=!qleft;
        //1.p,q在两边
        //2.p,q都在左边
        //3.p,q都在右边
        if((qleft&&pright)||(qright&&pleft))
        {
            return root;
        }
        else if(qleft&&pleft)
        {
            return lowestCommonAncestor(root->left,p,q);
        }
        else if(qright&&pright)
        {
            return lowestCommonAncestor(root->right,p,q);
        }
        else  //这种情况一般都走不到
        {
            return nullptr;
        }
    }
};

这里的精髓是pleft,pright,qleft,qright。

举个例子，如果p在左子树，那pright就不用找了，如果左子树上没找到，那他一定在右子树那里。