[C++知识库]2508. 添加边使所有节点度数都为偶数 c++

给你一个有 n?个节点的 无向?图，节点编号为?1?到?n?。再给你整数?n?和一个二维整数数组?edges?，其中?edges[i] = [ai, bi]?表示节点?ai 和?bi?之间有一条边。图不一定连通。

你可以给图中添加 至多?两条额外的边（也可以一条边都不添加），使得图中没有重边也没有自环。

如果添加额外的边后，可以使得图中所有点的度数都是偶数，返回?true?，否则返回?false?。

点的度数是连接一个点的边的数目。

示例 1：

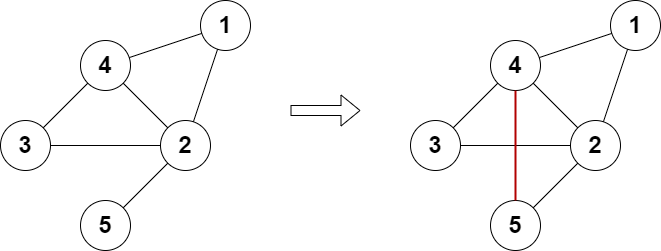
输入：n = 5, edges = [[1,2],[2,3],[3,4],[4,2],[1,4],[2,5]]
输出：true
解释：上图展示了添加一条边的合法方案。
最终图中每个节点都连接偶数条边。

示例 2：

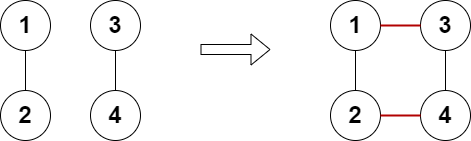
输入：n = 4, edges = [[1,2],[3,4]]
输出：true
解释：上图展示了添加两条边的合法方案。

示例 3：

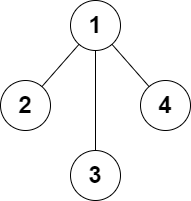
输入：n = 4, edges = [[1,2],[1,3],[1,4]]
输出：false
解释：无法添加至多 2 条边得到一个符合要求的图。

提示：

• 3 <= n <= 105
• 2 <= edges.length <= 105
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• 图中不会有重边

class Solution {
private:
    int vexs[100001];
    int vindex[4];
public:
    bool isPossible(int n, vector<vector<int>>& edges) {
        unordered_set<int> vex[n+1];
        for(auto e :edges){
            int x=e[0];
            int y=e[1];
            vex[x].insert(y);
            vex[y].insert(x);
        }
        vector<int> jishu;
        for(int i=1;i<=n;i++){
            if(vex[i].size()%2==1){
                jishu.push_back(i);
            }
        }
        int size=jishu.size();
        if(size==0){
            return true;
        }else if(size==2){
            int x=jishu[0],y=jishu[1];
            if(!vex[x].count(y)) return true;
            else{
                for(int k=1;k<=n;k++){
                    if(x!=k&&y!=k&&!vex[x].count(k)&&!vex[y].count(k))
                        return true;
                    else 
                        return false;
                }
            }
        }else if(size==4){
            int a=jishu[0],b=jishu[1],c=jishu[2],d=jishu[3];
            return !vex[a].count(b)&&!vex[c].count(d)||!vex[a].count(c)&&!vex[b].count(d)||!vex[a].count(d)&&!vex[c].count(b);
        }

       return false;
    }
};

?思路参照：力扣