[Java知识库]Java 归并排序思想及代码实现

目录

1.概念

2.算法思想

3.代码实现

4.复杂度

1.概念

归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

2.算法思想

（1）拆分：采用折半的方式将将给定数组拆分成为只有一个元素的子序列（将给定数组拆分为左右两个数组，再依次拆分左右两个数组，直到所有子序列都只含有一个元素）；

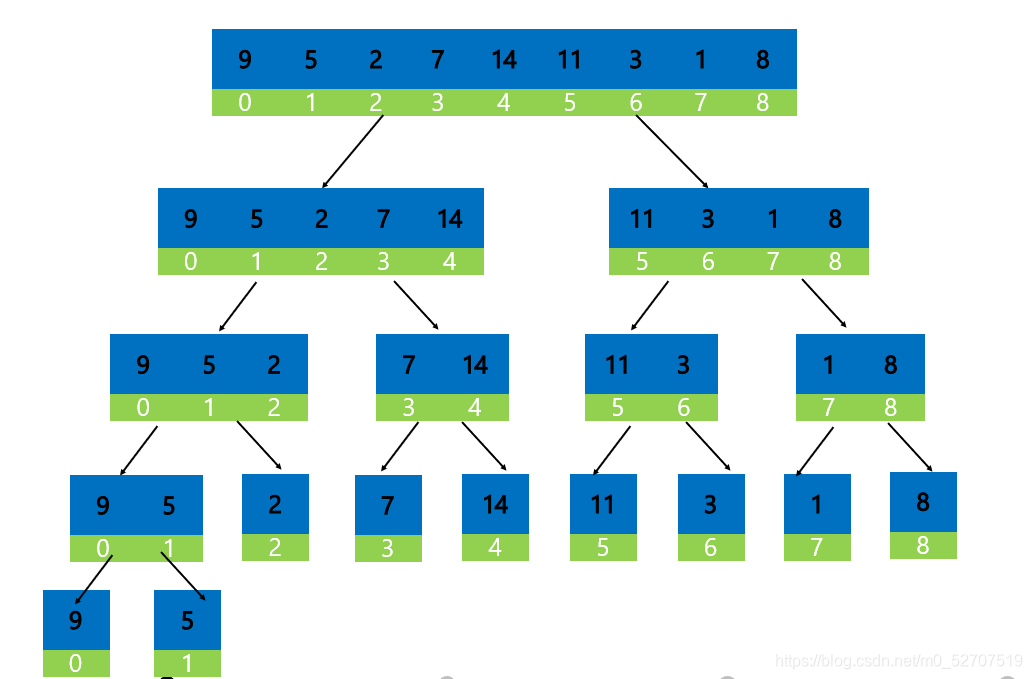
（2）合并：按照拆分的顺序反向进行合并，合并时选择此时左右两个数组中的最小值放在合并后数组的首位，再次比较新的左右两数组最小值放在第二位，以此类推完成数组的合并。

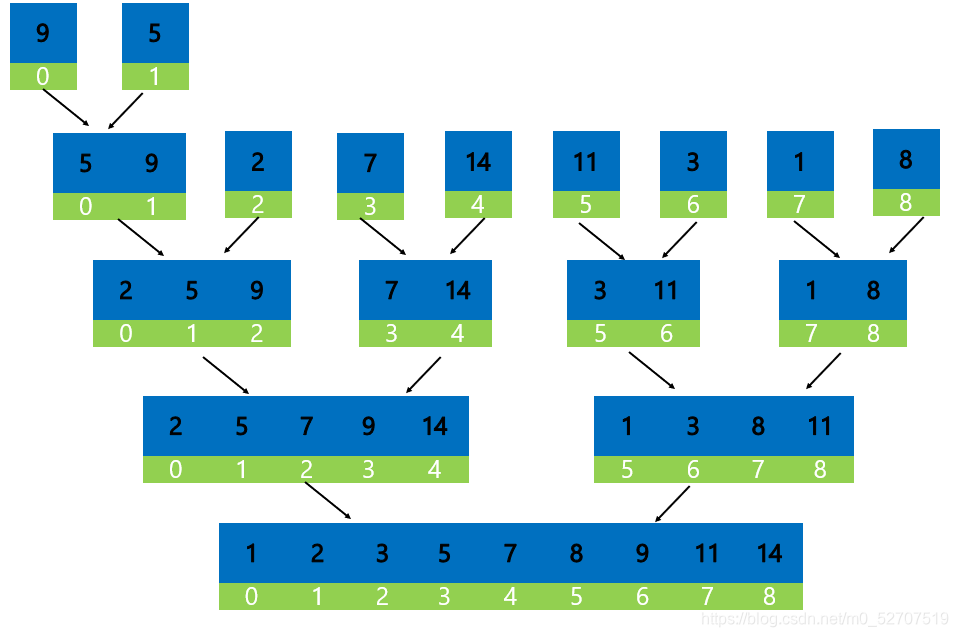
3.代码实现

public void resolve(int[] arr,int left,int right) {
		if (left <right) {//判断是否只有一个元素
			int mid = (left + right)/2;//中间点
			resolve(arr,left,mid);//递归划分左半区
			resolve(arr,mid+1,right);//递归划分右半区
			merge(arr,left,mid,right);//合并
		}
	}
	
	public void merge(int[] arr,int left,int mid,int right) {
		int[] arr1 = new int[arr.length];//创建一个和arr同等大小的空数组
		int l = left;//标记左半区第一个未排序元素
		int r = mid + 1;//标记右半区第一个未排序元素
		int index = 0;//临时数组元素下标
		//合并
		while (l <= mid && r <= right) {
			if (arr[l] > arr[r]) {//左半区元素大于右半区
				arr1[index++] = arr[r++];//右半区元素加入数组
			}else {//右半区大于左半区
				arr1[index++] = arr[l++];//左半区加入
			}
		}
		while(l <= mid) {
			arr1[index++] = arr[l++];//当左半区有元素剩余时，把剩余元素加入
		}
		while(r <= right) {
			arr1[index++] = arr[r++];//当右半区有元素剩余时，把剩余元素加入
		}
		System.arraycopy(arr1, 0, arr, left, right-left+1);//将arr1的值复制给arr
	}

4.复杂度