java 斐波那切数,汉诺塔和青蛙跳台阶及扩展问题
一、斐波那切数
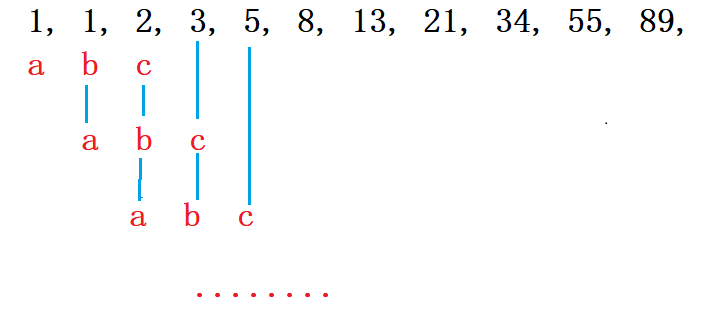
他是这样的一个数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
📜题目:求第n项斐波那切数。
📝思路:
规律是前两项之和等于第三项,从第三项开始算,前两项默认为1。
有两种方法,迭代和递归,先看迭代
??核心代码:
c=a+b;
a=b;
b=c;
💬迭代:
public class Test {
public static int fib(int n) {
if(n==1 || n==2) {
return 1;
}
int a=1;
int b=1;
int c=-1;
for(int i=3;i<=n;i++) {
c=a+b;
a=b;
b=c;
}
return c;
}
public static void main(String[] args) {
System.out.println(fib(4));
}
}
💬递归方法:
public class Test {
public static int fib(int n) {
if(n==1 || n==2) {
return 1;
}
return fib(n-1)+fib(n-2);
}
public static void main(String[] args) {
System.out.println(fib(4));
}
}
?两种方法谁好?
| 优点 | 缺点 | |
|---|---|---|
| 递归 | 代码简单 | 执行效率慢 |
| 迭代 | 代码稍微长一丢丢 | 执行快 |
?递归如果数字给大一点会怎么样尼?
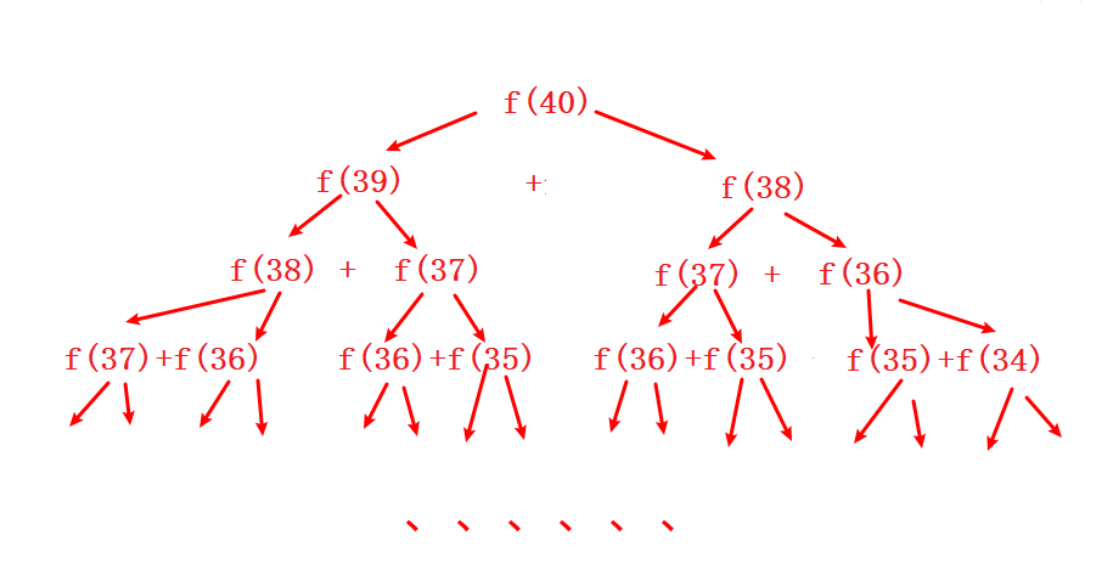
如图所示,会大量重复利用,一直递归,效率减慢。
?? 推荐使用:迭代方法
二、青蛙跳台阶
📜题目:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法?
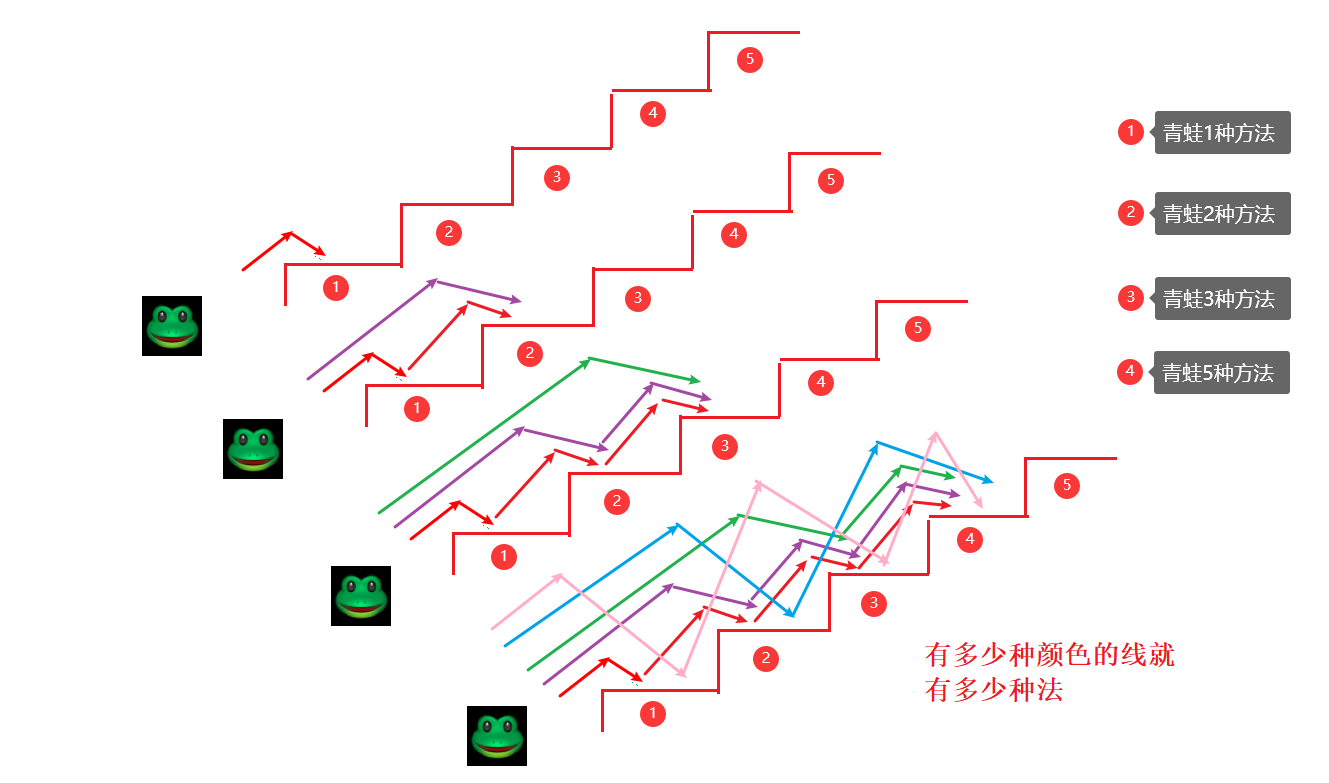
📝思路:
有图可知,不同台阶有多少种跳法是有规律的
1 2 3 5 这组数据是否跟上面斐波那契数相像,1+2=3,2+3=5,也是(n-1)+(n-2)得到第三项。
所以核心代码:
func(target-1)+func(target-2);
💬代码:
public class Test {
public static int func(int target) {
if(target==1) {//前两项默认为1,2
return 1;
}
if(target==2) {
return 2;
}
return func(target-1)+func(target-2);
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
System.out.println(func(n));
}
}
2.1青蛙跳台阶扩展
📜题目:若把条件修改成一次可以跳一级,也可以跳2级…也可以跳上n级呢?求该青蛙跳上一个n级的台阶(n为正整数)总共有多少种跳法。
这里用的是数学方法,找规律,这个比较简单易懂,不推荐用递归,时间复杂度是O(n^n) 😂😂😂
2.1.1找规律:
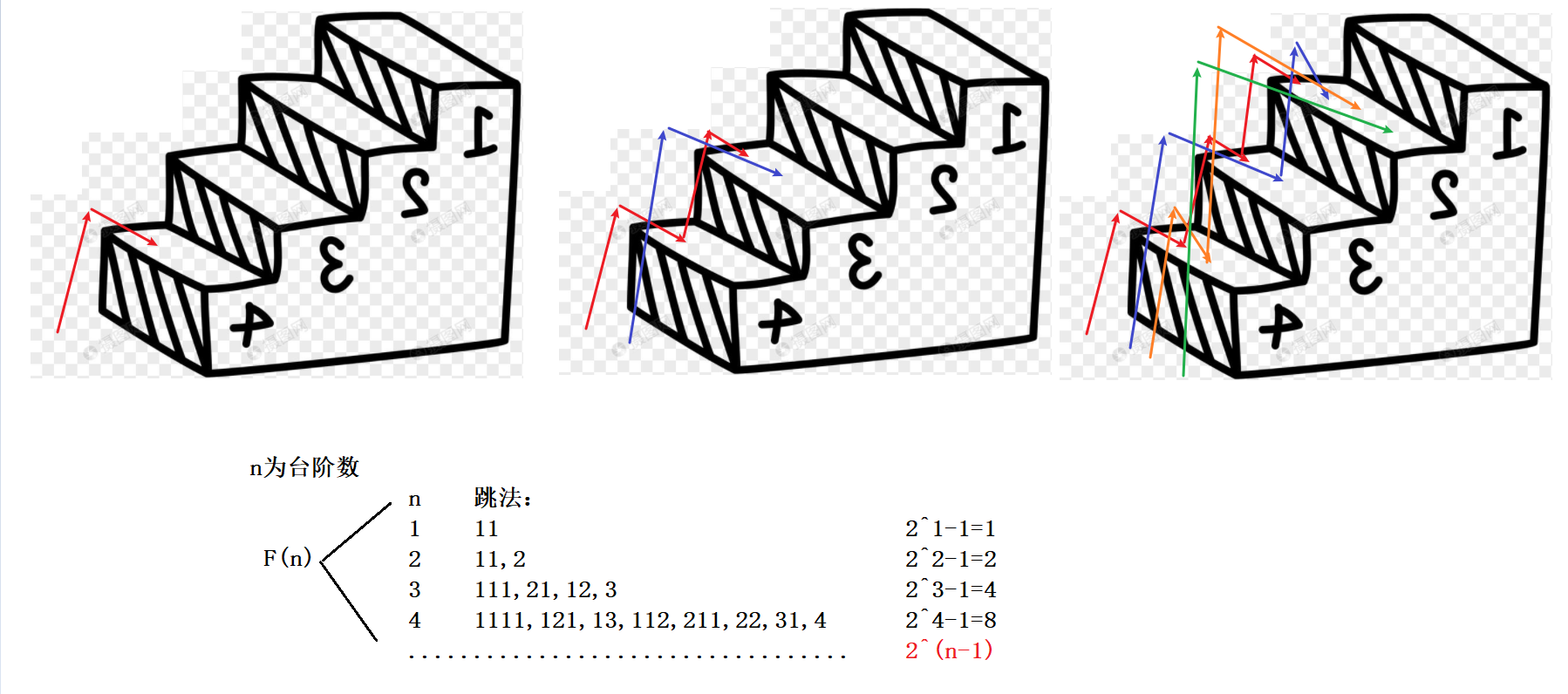
📝思路:
由图可以看出当你是1个台阶的时候只有一种跳法,2个台阶的时候2种跳法,三个台阶4种跳法…以此类推,可以得到一个公式2^(n-1)
??核心代码:
pow(2,n-1);
💬代码:
public class Test {
public static double jumpFloorII(int number) {
if (number == 1) {
return 1;
}
return pow(2, number - 1);
}
public static void main(String[] args) {
System.out.println(jumpFloorII(4));
}
}
2.1.2递推方法:
青蛙如果要跳上第五个台阶,那么就是要加上第一阶一直到第四台阶总的情况数,因为青蛙可以跳n阶嘛,最后还要加上青蛙可以直接跳上第五阶的情况
??核心代码:
a[i]=sum+1;
sum=sum+a[i];
💬代码:
public class Test {
public static int jumpFloor(int target) {
if(target==1) {
return 1;
}
int[] a=new int[target+1];
int sum=1;//存第一阶到n-1阶的所有情况
for(int i=2;i<=target;i++) {
a[i]=sum+1;//存第1阶到i-1阶的所有情况之和然后再加上青蛙可以从起点直接跳终点阶的情况
sum=sum+a[i];//每次台阶i++,都会更新1到i阶情况数
}
return a[target];
}
public static void main(String[] args) {
System.out.println(jumpFloor(4));
}
}
2.1.3大佬的解法😎
① f(n) = f(n-1) + f(n-2) +f(n-3) + … + f(2) + f(1)
② f(n-1) = f(n-2) +f(n-3) + … + f(2) + f(1)
由①②得,f(n) = 2f(n-1);
public static int jumpFloor3(int target) {
if (target == 1) {
return 1;
} else {
return 2 * jumpFloor3(target - 1);
}
}
?? 推荐使用:找规律和递推,不建议使用递归
三、汉诺塔
题目:汉诺塔问题是一个经典的问题。汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。
? 问应该如何操作?
先不拿64个盘子,先拿三个盘子
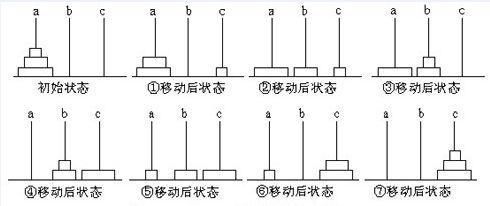
📝思路:
有图可知,要想把三个大小不同的盘子移动到c位置上
A->C A->B C->B A->C B->A B->C A->C 2^3 -1=7
那么两个盘子的时候:
A->B A->C B->C 2^2 -1=3
一个盘子的时候:
A->C 2^1 -1=1
如果是64个盘子,根据以上规律可得出的式子2n-1,所以64个盘子的时候就是264-1=18,446,744,073,709,551,615 ,就会有这么多种移法,所以我们用递归思路,剩下的交给计算机就行了。
??核心代码
if(n==1) {
move(pos1,pos3);
}else {
hanoiTower(n-1,pos1,pos3,pos2);
move(pos1,pos3);
hanoiTower(n-1,pos2,pos1,pos3);
}
💬代码:
/**
*
* @param n 当前的盘子个数
* @param pos1 A
* @param pos2 B
* @param pos3 C
*/
public class Test {
public static void move(char pos1,char pos3) {
System.out.print(pos1 + "->" +pos3 + " ");
}
public static void hanoiTower (int n,char pos1,char pos2,char pos3) {
if(n==1) {
move(pos1,pos3);
}else {
hanoiTower(n-1,pos1,pos3,pos2);
move(pos1,pos3);
hanoiTower(n-1,pos2,pos1,pos3);
}
}
public static void main(String[] args) {
hanoiTower(3,'A','B','C');
System.out.println();
}
}