[Java知识库]JAVA实现图的构建、BFS、DFS（分邻接矩阵存储与邻接表存储）

一、文章内容

1、以邻接矩阵存储的图（构建、BFS、DFS）

2、以邻接表存储的图（构建、BFS、DFS）

3、广度优先遍历用到的队列

二、以邻接矩阵存储的图（构建、BFS、DFS）

1、AMGraph.java

import java.util.Scanner;

// 邻接矩阵存储的图，以无向网为例
public class AMGraph {
    private static final int MAXINT = 10000;// 作为极大值
    private static final int MAXNUM = 100;// 顶点数组的最大容量
    private char[] vexs;// 顶点数组
    private int[][] arcs;// 临界矩阵
    private int vexNum;// 顶点个数
    private int arcNum;// 边个数
    private boolean[] visited;// 用于遍历时顶点是否被访问的标志，每次遍历前需要重置，数组中元素全部置为false

    public void createAMGraph(){
        Scanner in = new Scanner(System.in);

        // 初始化顶点数和边数
        System.out.println("请输入顶点数和边数，以空格隔开：");
        String line01 = in.nextLine();
        String[] nums = line01.split(" ");
        vexNum = Integer.valueOf(nums[0]);
        arcNum = Integer.valueOf(nums[1]);

        // 初始化顶点数组
        vexs = new char[MAXNUM];
        System.out.println("请输入顶点，以空格隔开：");
        String line02 = in.nextLine();
        char[] temp = line02.replaceAll(" ", "").toCharArray();
        for (int i=0; i<temp.length; ++i){
            vexs[i] = temp[i];
        }

        // 初始化邻接矩阵，值全部设置为-1
        arcs = new int[vexNum][vexNum];
        for (int i=0; i<vexNum; ++i){
            for (int j=0; j<vexNum; ++j){
                arcs[i][j] = MAXINT;
            }
        }

        // 为边赋权值
        for (int k=0; k<arcNum; ++k){
            System.out.println("请输入两个邻接顶点及其边的权值，以空格隔开：");
            String line03 = in.nextLine();
            String[] strs = line03.split(" ");
            char v1 = strs[0].charAt(0);
            char v2 = strs[1].charAt(0);
            int weight = Integer.valueOf(strs[2]);

            // 获取v1、v2两个顶点在顶点数组中的下标
            int i = locateVex(vexs, v1);
            int j = locateVex(vexs, v2);

            // 为邻接矩阵设值
            this.arcs[i][j] = weight;
            this.arcs[j][i] = weight;
        }
    }

    // 获取指定顶点在顶点数组中的下标
    private int locateVex(char[] vexs, char v) {
        for (int i=0; i<vexs.length; ++i){
            if (v == vexs[i]){
                return i;
            }
        }
        System.out.println("输入顶点有误，程序退出！");
        System.exit(-1);
        return -1;
    }

    /**
     * 深度优先遍历
     * @param g 待遍历的图（以邻接矩阵存储的图）
     * @param start 开始遍历的顶点在顶点数组中的下标
     */
    public void dfsTraverse(AMGraph g, int start){
        this.visited[start] = true;
        System.out.print(g.getVexs()[start] + " ");
        for (int i=0; i<g.getVexNum(); ++i){// 遍历邻接矩阵中顶点所在的行
            if (g.getArcs()[start][i]!=MAXINT && !this.visited[i]){
                dfsTraverse(g, i);
            }
        }
    }

    // 广度优先遍历
    public void bfsTraverse(AMGraph g, int start){
        Queue<Character> queue = new Queue<>(g.getVexNum()+1);

        // 入队
        queue.enter(g.getVexs()[start]);
        visited[start] = true;

        while ( !queue.is_empty() ){
            char c = queue.out();// 出队
            System.out.print(c + " ");
            start = locateVex(g.getVexs(), c);

            for (int i=0; i<g.getVexNum(); ++i){
                if (g.getArcs()[start][i]!=MAXINT && !visited[i]){
                    queue.enter(g.getVexs()[i]);// 入队
                    visited[i] = true;
                }
            }
        }
    }

    // 输出邻接矩阵
    public void showAM(){
        for (int i=0; i<vexNum; ++i){
            for (int j=0; j<vexNum; ++j){
                System.out.print(arcs[i][j] + "\t\t\t\t\t");
            }
            System.out.println();
        }
    }

    public char[] getVexs() {
        return vexs;
    }

    public void setVexs(char[] vexs) {
        this.vexs = vexs;
    }

    public int[][] getArcs() {
        return arcs;
    }

    public void setArcs(int[][] arcs) {
        this.arcs = arcs;
    }

    public int getVexNum() {
        return vexNum;
    }

    public void setVexNum(int vexNum) {
        this.vexNum = vexNum;
    }

    public int getArcNum() {
        return arcNum;
    }

    public void setArcNum(int arcNum) {
        this.arcNum = arcNum;
    }

    public boolean[] getVisited() {
        return visited;
    }

    public void setVisited(boolean[] visited) {
        this.visited = visited;
    }
}

?2、Test.java

public class Test {
    public static void main(String[] args) {
        AMGraph g = new AMGraph();

        // 创建邻接矩阵存储的图
        g.createAMGraph();

        // 输出邻接矩阵
        System.out.println("邻接矩阵如下：");
        g.showAM();

        // 深度优先遍历
        g.setVisited(new boolean[g.getVexNum()]);
        System.out.print("深度优先遍历结果：");
        g.dfsTraverse(g, 0);
        System.out.println();

        // 深度优先遍历
        g.setVisited(new boolean[g.getVexNum()]);
        System.out.print("广度优先遍历结果：");
        g.bfsTraverse(g, 0);
        System.out.println();
    }
}

3、测试结果

?

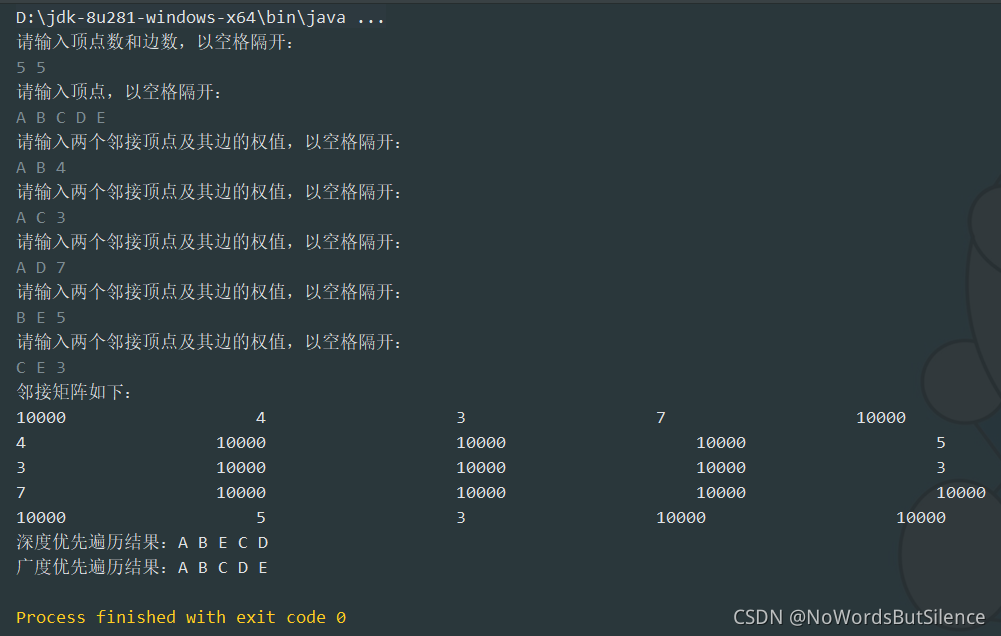
三、以邻接表存储的图（构建、BFS、DFS）

1、ALGraph.java

import java.util.Scanner;

// 邻接表存储的图
public class ALGraph {
    private static final int MVNUM = 100;
    private VNode[] vexs = new VNode[MVNUM];
    private int vexNum;
    private int arcNum;
    private int[] visited;// 顶点访问标志数组，每次遍历时须重新初始化，数组中元素全部置为0

    // 构建图
    public void createALGraph(){
        Scanner in = new Scanner(System.in);

        // 初始化顶点个数与边个数
        System.out.println("请输入顶点个数和边的个数，以空格隔开：");
        String line01 = in.nextLine().replaceAll(" ", "");
        vexNum = (int)line01.charAt(0)-48;
        arcNum = (int)line01.charAt(1)-48;

        // 初始化VNode[]的顶点信息
        System.out.println("请输入顶点字符，以空格隔开：");
        String line02 = in.nextLine();
        char[] chars = line02.replaceAll(" ", "").toCharArray();
        for (int i=0; i<vexNum; ++i){
            VNode node = new VNode();
            node.setC(chars[i]);
            vexs[i] = node;
        }

        // 初始化VNode[]中边节点信息
        for (int k=0; k<arcNum; ++k){
            System.out.println("请输入互为邻接点的顶点及对应的权值，以空格隔开：");
            String line03 = in.nextLine();
            String[] strings = line03.split(" ");
            char v1 = strings[0].charAt(0);
            char v2 = strings[1].charAt(0);
            int weight = Integer.valueOf(strings[2]);

            // 定位顶点在VNode中的下标
            int i = locateVex(vexs, v1);
            int j = locateVex(vexs, v2);

            // 创建边节点，采用头插法连接到链表中
            AdjNode node01 = new AdjNode();// 连接到下标为i的指针域
            node01.setAdjVex(j);
            node01.setWeight(weight);
            node01.setNextArc(vexs[i].getFirstArc());
            vexs[i].setFirstArc(node01);
            AdjNode node02 = new AdjNode();// 连接到下标为j的指针域
            node02.setAdjVex(i);
            node02.setWeight(weight);
            node02.setNextArc(vexs[j].getFirstArc());
            vexs[j].setFirstArc(node02);
        }
    }

    // 定位顶点下标
    private int locateVex(VNode[] g, char v2) {
        for (int i=0; i<vexNum; ++i){
            if (g[i].getC() == v2){
                return i;
            }
        }
        System.out.println("输入节点信息有误，程序退出！");
        System.exit(-1);
        return -1;
    }

    // 输出邻接表
    public void showAL(){
        for (int i=0; i<vexNum; ++i){
            System.out.print(vexs[i].getC());
            AdjNode temp = vexs[i].getFirstArc();
            while (temp != null){
                System.out.print("-->" + temp.getAdjVex());
                temp = temp.getNextArc();
            }
            System.out.println();
        }
    }

    // 深度优先遍历
    public void dfsTraverse(ALGraph g, int start){
        visited[start] = 1;
        System.out.print(g.getVexs()[start].getC() + " ");

        AdjNode temp = g.getVexs()[start].getFirstArc();
        while (temp != null){
            if (visited[temp.getAdjVex()] == 0){
                start = temp.getAdjVex();
                dfsTraverse(g, start);
            }
            temp = temp.getNextArc();
        }
    }

    // 广度优先遍历
    public void bfsTraverse(ALGraph g, int start){
        Queue<VNode> queue = new Queue<>(g.getVexNum());

        // 遍历
        queue.enter(g.getVexs()[start]);
        visited[start] = 1;
        while ( !queue.is_empty() ){
            VNode node = queue.out();// 出队一个元素
            System.out.print(node.getC() + " ");

            // 入队邻接点
            AdjNode temp = node.getFirstArc();
            while (temp != null){
                start = temp.getAdjVex();
                if (visited[start] == 0){
                    queue.enter(g.getVexs()[start]);
                    visited[start] = 1;
                }
                temp = temp.getNextArc();
            }
        }
    }

    // getter and setter
    public VNode[] getVexs() {
        return vexs;
    }

    public void setVexs(VNode[] vexs) {
        this.vexs = vexs;
    }

    public int getVexNum() {
        return vexNum;
    }

    public void setVexNum(int vexNum) {
        this.vexNum = vexNum;
    }

    public int getArcNum() {
        return arcNum;
    }

    public void setArcNum(int arcNum) {
        this.arcNum = arcNum;
    }

    public int[] getVisited() {
        return visited;
    }

    public void setVisited(int[] visited) {
        this.visited = visited;
    }
}

// 数组元素
class VNode{
    private char c;
    private AdjNode firstArc;

    public char getC() {
        return c;
    }

    public void setC(char c) {
        this.c = c;
    }

    public AdjNode getFirstArc() {
        return firstArc;
    }

    public void setFirstArc(AdjNode firstArc) {
        this.firstArc = firstArc;
    }
}

// 边节点
class AdjNode{
    private int adjVex;
    private int weight;
    private AdjNode nextArc;

    public int getAdjVex() {
        return adjVex;
    }

    public void setAdjVex(int adjVex) {
        this.adjVex = adjVex;
    }

    public int getWeight() {
        return weight;
    }

    public void setWeight(int weight) {
        this.weight = weight;
    }

    public AdjNode getNextArc() {
        return nextArc;
    }

    public void setNextArc(AdjNode nextArc) {
        this.nextArc = nextArc;
    }
}

2、Test.java

public class Test {
    public static void main(String[] args) {
        ALGraph g = new ALGraph();

        // 构建图
        g.createALGraph();

        // 输出邻接表
        System.out.println("邻接表如下：");
        g.showAL();

        // 深度优先遍历图
        System.out.print("深度优先遍历：");
        g.setVisited(new int[g.getVexNum()]);
        g.dfsTraverse(g, 0);
        System.out.println();

        // 广度优先遍历
        g.setVisited(new int[g.getVexNum()]);
        System.out.print("广度优先遍历：");
        g.bfsTraverse(g, 0);
        System.out.println();
    }
}

3、测试结果

?

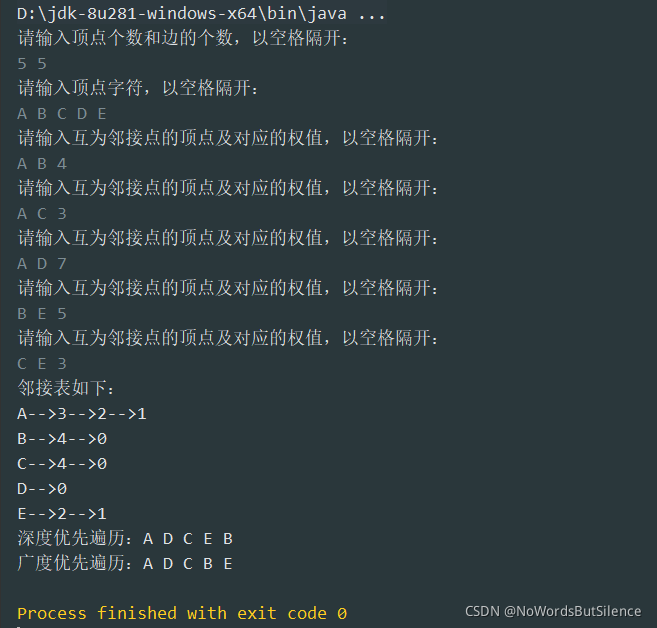
四、广度优先遍历用到的队列

public class Queue<E> {
    private E[] arr;
    private int len;
    private int front = 0;
    private int rear = 0;

    // 初始化

    public Queue(int len) {
        this.len = len;
        this.arr = (E[]) new Object[len];
    }

    // 队列是否已满
    public boolean is_full(){
        return (front+1)%len==rear;
    }

    // 队列是否为空
    public boolean is_empty(){
        return front==rear;
    }

    // 入队
    public void enter(E e){
        if ( is_full() ){
            return;
        }
        front = (front+1)%len;
        arr[front] = e;
    }

    // 出队
    public E out(){
        if ( is_empty() ){

        }
        rear = (rear+1)%len;
        return arr[rear];
    }
}