[Java知识库]Java实现寻找二维数组的鞍点

一、题目描述：

定义一个二维数组用于存储一个4×4 矩阵的元素值，并找出这个矩阵的所有鞍点，然后输出鞍点的位置及值。

二、鞍点解释

• ①在微分方程中，沿着某一方向是稳定的，另一条方向是不稳定的奇点，叫做鞍点。
• ②在泛函中，既不是极大值点也不是极小值点的临界点，叫做鞍点。
• ③在矩阵中，一个数在所在行中是最大值，在所在列中是最小值，则被称为鞍点。
• ④在物理上要广泛一些，指在一个方向是极大值，另一个方向是极小值的点。

三、分析

鞍点就是二维数组中一个元素既是它所在行的最大值，又是所在列的最小值。

• 算法思路：
  ①先寻找每一行的最大值
  ②记录每一行最大数的所在的列
  ③判断最大值在他所在的列是否也是最小值
  ④若是鞍点则输出鞍点所在位置及值，若不存在鞍点输出“没有鞍点”。

四、代码

package com.lyp.test;

import java.util.Scanner;

public class findSaddlePoint {

    public static void main(String[] args) {
        int s,min,max,count = 0;
        int[] a = new int[4];
        Scanner scanner = new Scanner(System.in);
        //定义4*4数组
        int[][] array = new int[4][4];
        //接收数组的输入
        System.out.println("请输入数组元素：");
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 4; j++) {
                System.out.print("请输入第"+(i+1)+"行第"+(j+1)+"个元素：");
                array[i][j] = scanner.nextInt();
            }
        }
        //打印数组
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 4; j++) {
                System.out.print(array[i][j]+"   ");
            }
            System.out.println();
        }
        //寻找鞍点
        for (int i = 0; i < 4; i++) {
            max = array[i][0];
            for (int j = 0; j < 4; j++) { //找每行的最大值
                if (array[i][j] > max){
                    max = array[i][j];
                }
            }
            s = 0;
            for (int j = 0; j < 4; j++) { //将最大值所在的列存入a[]中
                if (array[i][j] == max){
                    a[s] = j;
                    s++;    //s的值是最大值的个数
                }
            }
            min = max;
            for (int j = 0; j < s; j++) { //有几个最大值，就进行几次循环
                for (int k = 0; k < 4; k++) { //判断这个行的最大值是不是列最小
                    if(min > array[k][a[j]]) { //如果不是，则判断下一个
                        break;
                    }
                    if (k == 3){ //说明是鞍点
                        System.out.println("鞍点为第"+(i+1)+"行第"+(a[j] + 1)+"列的元素："+array[i][a[j]]);
                        count++;
                    }
                }
            }
        }
        if(count == 0){
            System.out.println("没有鞍点");
        }

    }
}

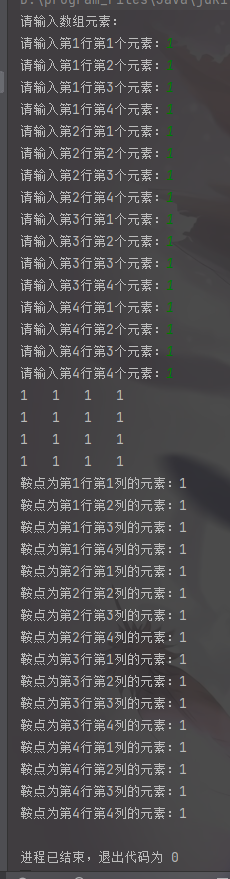
五、输出结果

示例一：

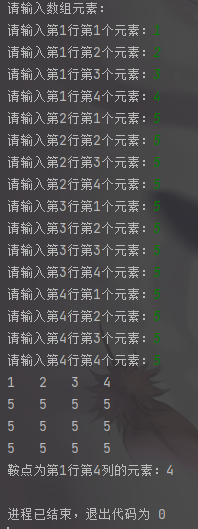
示例二：

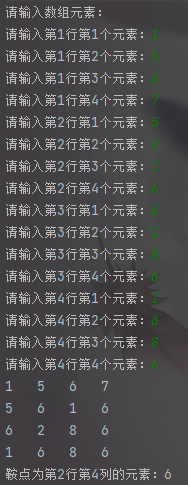
示例三：

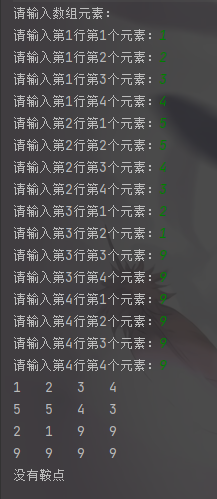
示例四：