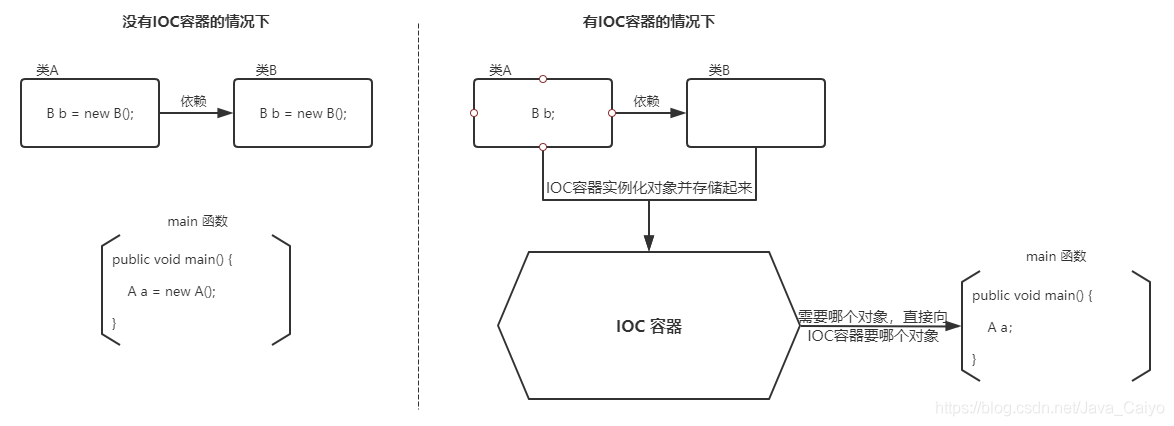
二、IOC 解决了什么问题
IOC 主要解决的是对象之间的耦合问题。
例如:现有一个针对User的操作,利用 Service 和 Dao 两层结构进行开发
在没有使用IOC思想的情况下,Service 层想要使用 Dao层的具体实现的话,需要通过new关键字在 UserServiceImpl 中手动 new出 IUserDao 的具体实现类 UserDaoImpl(不能直接new接口类)。
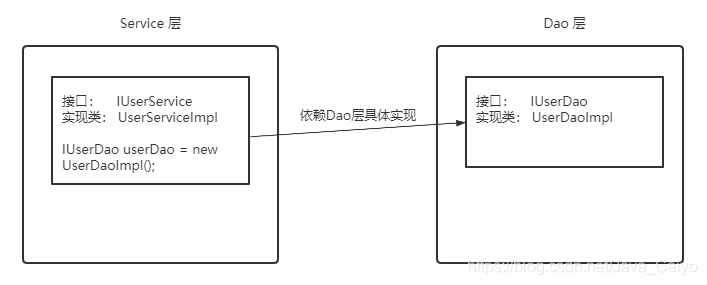
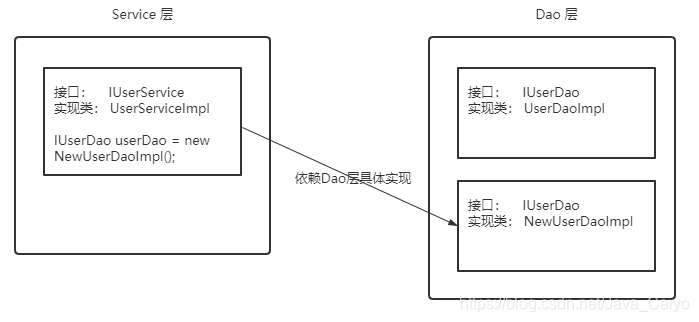
很完美,这种方式也是可以实现的,但是我们想象一下如下场景:开发过程中突然接到一个新的需求,针对对IUserDao 接口开发出另一个具体实现类。因为Server层依赖了IUserDao的具体实现,所以我们需要修改UserServiceImpl中new的对象。如果只有一个类引用了IUserDao的具体实现,可能觉得还好,修改起来也不是很费力气,但是如果有许许多多的地方都引用了IUserDao的具体实现的话,一旦需要更换IUserDao的实现方式,那修改起来将会非常的头疼。
使用IOC的思想,我们将对象的控制权(创建、管理)交有IOC容器去管理,我们在使用的时候直接向IOC容器 “要” 就可以了
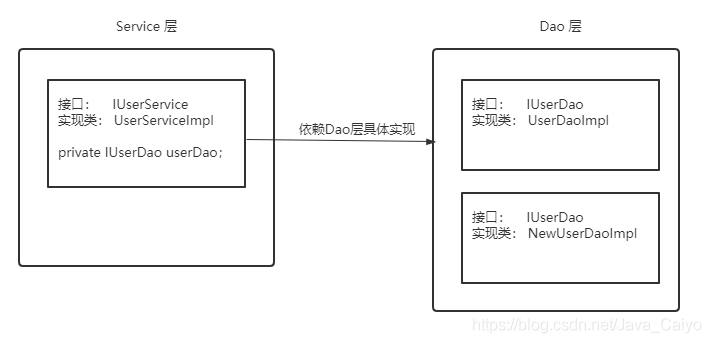
三、IOC 和 DI 的区别
IOC 和 DI 描述的是同一件事情(对象实例化以及依赖关系的维护),只不过角度不同。
IOC (Inversion of control ) 控制反转/反转控制。是站在对象的角度,对象实例化以及管理的权限(反转)交给了容器。
DI (Dependancy Injection)依赖注入。是站在容器的角度,容器会把对象依赖的其他对象注入(送进去)。例如:对象A 实例化过程中因为声明了一个B类型的属性,那么就需要容器把B对象注入到A中。
四、什么是AOP
AOP:Aspect oriented programming 面向切面编程,AOP是 OOP(面向对象编程)的一种延续,下面我们先看一个OOP的例子。
例如:现有三个类,Horse、Pig、Dog,这三个类中都有 eat 和 run 两个方法。
通过OOP思想中的继承,我们可以提取出一个 Animal 的父类,然后将 eat 和 run 方法放入父类中,Horse、Pig
【一线大厂Java面试题解析+后端开发学习笔记+最新架构讲解视频+实战项目源码讲义】
浏览器打开:qq.cn.hn/FTf 免费领取
、Dog通过继承Animal类即可自动获得 eat 和 run 方法。这样将会少些很多重复的代码。

OOP编程思想可以解决大部分的代码重复问题。但是有一些问题是处理不了的。比如在父类Animal 中的多个方法的相同位置出现了重复的代码,OOP就解决不了。
COPY
/**
- 动物父类
*/
public class Animal {
/** 身高 */
private String height;
/** 体重 */
private double weight;
public void eat() {
// 性能监控代码
long start = System.currentTimeMillis();
// 业务逻辑代码
System.out.println(“I can eat…”);
// 性能监控代码
System.out.println(“执行时长:” + (System.currentTimeMillis() - start)/1000f + “s”);
}
public void run() {
// 性能监控代码
long start = System.currentTimeMillis();
// 业务逻辑代码
System.out.println(“I can run…”);
// 性能监控代码
System.out.println(“执行时长:” + (System.currentTimeMillis() - start)/1000f + “s”);
}
}
这部分重复的代码,一般统称为 横切逻辑代码。

横切逻辑代码存在的问题:
- 代码重复问题
- 横切逻辑代码和业务代码混杂在一起,代码臃肿,不变维护
AOP 就是用来解决这些问题的
AOP 另辟蹊径,提出横向抽取机制,将横切逻辑代码和业务逻辑代码分离
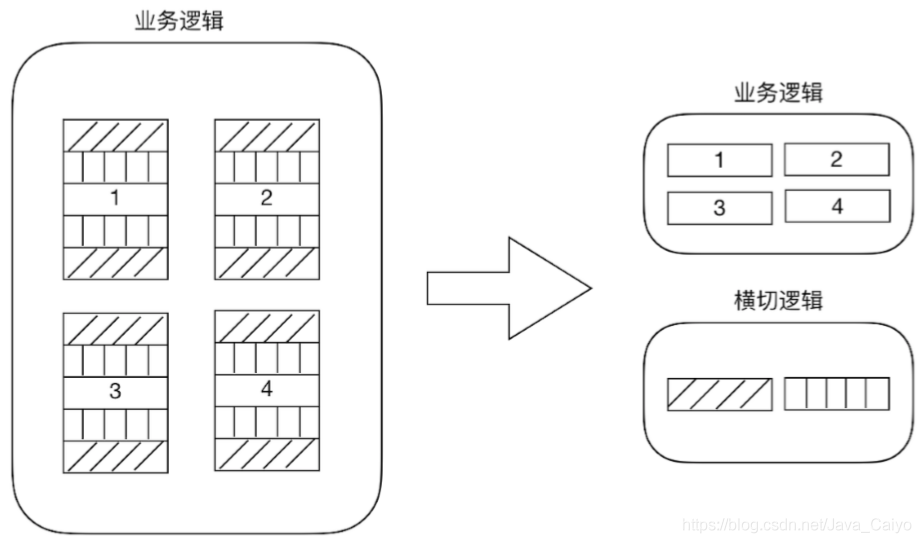
代码拆分比较容易,难的是如何在不改变原有业务逻辑的情况下,悄无声息的将横向逻辑代码应用到原有的业务逻辑中,达到和原来一样的效果。
五、AOP解决了什么问题
通过上面的分析可以发现,AOP主要用来解决:在不改变原有业务逻辑的情况下,增强横切逻辑代码,根本上解耦合,避免横切逻辑代码重复。
六、AOP为什么叫面向切面编程
切:指的是横切逻辑,原有业务逻辑代码不动,只能操作横切逻辑代码,所以面向横切逻辑
代码,根本上解耦合,避免横切逻辑代码重复。
六、AOP为什么叫面向切面编程
切:指的是横切逻辑,原有业务逻辑代码不动,只能操作横切逻辑代码,所以面向横切逻辑