一.方法的定义与使用

//方法定义
public static 返回值声明 方法名称(参数类型 参数名称 ...){
   方法体代码;
   [return 返回值];
}

//方法调用
返回值变量=方法名称(实参...);

在没有返回值的方法中使用return; 表示提前结束方法的调用。
java中没有函数声明的概念，一旦定义一个方法就必须写它的实现。
调用该方法与该方法定义的位置无关，可以在方法实现代码之前调用该方法。
java方法的参数传递只有值传递，只是将实参的值复制一份给形参。

二.方法的重载

方法重载定义:在同一个类中，定义了若干个方法名称相同，参数列表不同（参数类型和个数），与返回值无关，这样的一组方法称为重载方法。

应用：println方法中可以接收所有类型。

代码示例：

public class Test {
    public static void main(String[] args) {
        int a=10;
        int b=20;
        int ret=add(a,b);
        System.out.println(ret);

        double a1=10.2;
        double b1=1.0;
        double ret1=add(a1,b1);
        System.out.println(ret1);

        double a2=1.2;
        double b2=3.5;
        double c2=4.0;
        double ret2=add(a2,b2,c2);
        System.out.println(ret2);
    }
    public static int add(int x,int y){
        return x+y;
    }
    public static double add(double x,double y){
        return x+y;
    }
    public static double add(double x,double y,double z){
        return x+y+z;
    }
}

三.方法递归

那些场景下可以考虑递归：

一个大问题可以拆分为多个子问题的解；
拆分后的子问题和原问题除了数据规模不一样，他们的解决思路完全相同；
存在递归终止条件。

递归执行过程分析:

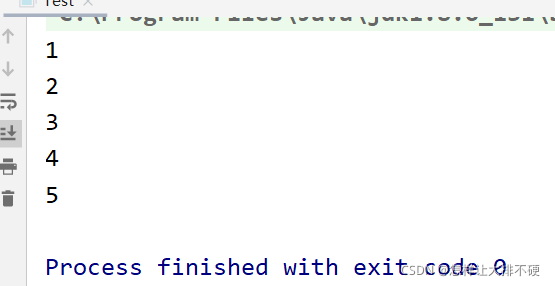
?示例代码：

 public static void main(String[] args) {
        //定义一个方法，按最高位到最低位输出其各个位数的数字
        int num=12345;
        printNum(num);
    }
    public static void printNum(int num){
        if(num>9){
            printNum(num/10);
        }
        System.out.println(num%10);
    }

?结果：

四.数组的基本用法

1.数组定义：存放相同数据类型的集合。

2.创建数组：

//动态初始化
数据类型[] 数组名称 = new 数据类型[] {初始化数据};
int[] arr=new int[] {1,2,3};
int[] arr=new int[3];

//静态初始化
数据类型[] 数组名称 = {初始化数据};
int[] arr={1,2,3};

3.数组的访问与长度：

使用arr.length能够获取到数组的长度。
数组长度为[0,arr.length-1]。
数组下标从0开始？因为在数组中是根据数组的索引来取得数组元素的，索引：0 - length-1，下标从0开始，数组索引就是相对于第一个元素的偏移量。

4.数组遍历

for-each是for循环的另一种使用方法，只遍历不修改数组元素：

 int[] arr={1,2,3};
        for (int x:
             arr) {
            System.out.println(x);
        }
//执行结果
1
2
3

5.理解引用数据类型

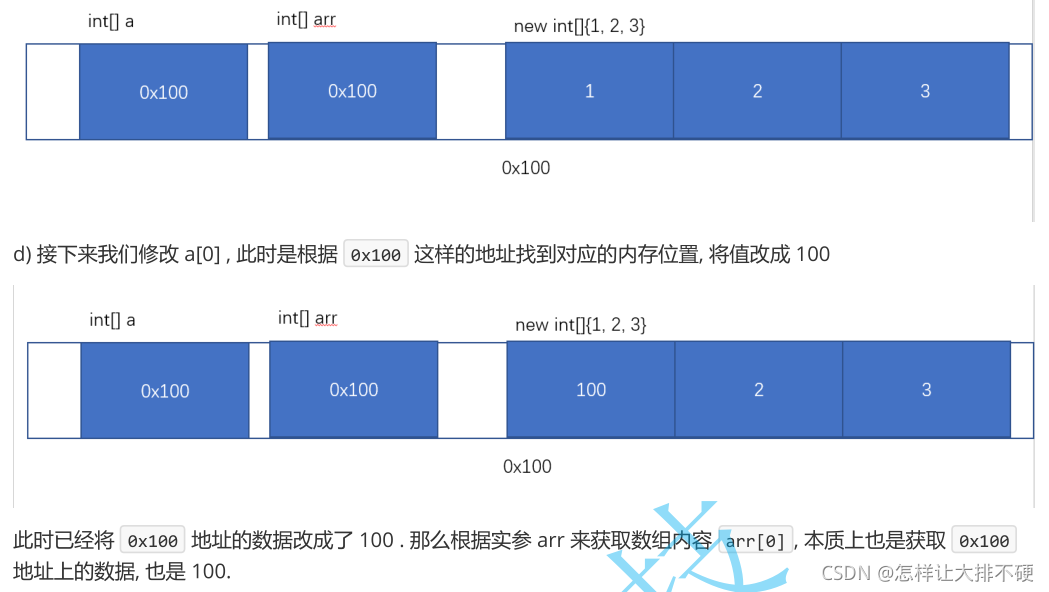
引用只是给对象起了一个别名而已，保存的是对象的地址
对象：new出来的都是对象——实实在在存在的东西
局部变量和引用都保存在栈上，new出来的对象保存在堆上?

6.数组的工具类

Java中提供了java.util.Arrays包中包含了一些数组的常用方法:

Arrays.toString(数组名) :将数组转换成字符串。
Arrays.copyOf(原数组名,拷贝后的新数组长度) :拷贝数组，深拷贝，即又创建了一个新数组。
Arrays.copyOfRange(原数组名,from,to) ：拷贝某个范围，[from,to)左闭右开区间。

五.二分查找

必须是有序数组！！！

代码如下：

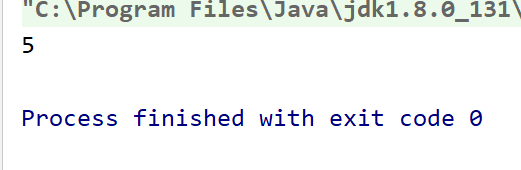
class Homework {
    public static void main(String[] args) {
      int[] arr={1,2,3,4,5,6,7,8,9,10,18};
      System.out.println(binarySearch1(arr,6));
  }
   public static int binarySearch1(int[] arr,int toFind){
        return binarySearch2(arr,toFind,0,arr.length-1);
    }
    public static int binarySearch2(int[] arr,int toFind,int left,int right){
        while(left<=right){
            int mid=(left+right)/2;
            if(toFind<arr[mid]){
                return binarySearch2(arr,toFind,left,mid-1);
            }else if(toFind>arr[mid]){
                return binarySearch2(arr, toFind, mid+1, right);
            }else{
                return mid;
            }
        }
        return -1;
    }
}

结果为：