目录
一、深浅拷贝
? ? ? ? 1.如何对DateTime对象进行复制
? ? ? ? DateTime source=new DateTime(...);?
? ? ? ? 方法一:DateTime dest=source?分析:完全不可以实现,仅仅创建新的引用dest指向source
? ? ? ? 方法二:DateTime dest=source.copy();
? ? ? ? ? ? ? ? ? ? ? ? public DateTime copy(){? ? ? ? ? ? ? ? ? 分析:换汤不换药,本质与方法一相同
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? return this;
?????????????????????????}?
? ? ? ? 方法三:DateTime dest=source,copy()
? ? ? ? ? ? ? ? ? ? ? ? public DateTime copy(){? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?DateTime dt=new DateTime();
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? dt.date=this.date;
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? dt.time=date.time;
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? return dt;
?????????????????????????}
分析:虽然完成了对象的复制,dest和source也确实指向不同的对象,但依旧藕断丝连
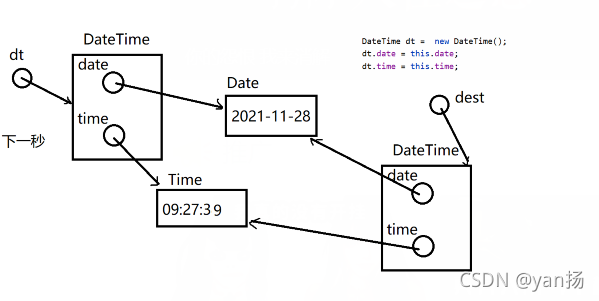
?方法四:DateTime dest=source,copy()
????????????????
????????? public DateTime copy(){? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?DateTime dt=new DateTime();
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? dt.date=new Date(this,date)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? dt.time=new Time(this,time)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ?return dt;
?????????????????????????}
分析:深拷贝彻底分离
二、DateTime类整合
// 约束要求
// 1. 年只能从 1000 到 3000
// 2. 月只能是 1 - 12
// 3. 天根据每个月的不同,天应该不同
public class Date {
private int year;
private int month;
private int day;
public Date(Date date) {
// 不需要做规范性检查了
this.year = date.year;
this.month = date.month;
this.day = date.day;
}
public int getYear() {
return year;
}
public int getMonth() {
return month;
}
public int getDay() {
return day;
}
public Date(int year, int month, int day) {
if (!checkYear(year)) {
throw new RuntimeException("year 必须是 [1000, 3000]: year = " + year);
}
if (!checkMonth(month)) {
throw new RuntimeException("month 必须是 [1, 12]: month = " + month);
}
if (!checkDay(year, month, day)) {
throw new RuntimeException("day 必须是符合范围");
}
// 保证数据一定符合要求,可以保存属性中了
this.year = year;
this.month = month;
this.day = day;
}
public String toString() {
return String.format("%04d-%02d-%02d", year, month, day);
}
public void 往前一天() {
day--;
// 如果 day 是合法 (>= 1) 结束
if (day > 0) {
return;
}
month--;
// 如果 month 不合法(< 1),修复 month
// year-- month=12
if (month == 0) {
year--;
month = 12;
}
//day = 和 month 有关;
day = 根据月取边界(year, month);;
}
public void 往后一天() {
day++;
int dayBound = 根据月取边界(year, month);
if (day <= dayBound) {
return;
}
month++;
day = 1;
if (month <= 12) {
return;
}
year++;
month = 1;
}
private static int 根据月取边界(int year, int month) {
if (month == 2) {
return isLeapYear(year) ? 29 : 28;
} else {
return DAY_OF_MONTH[month - 1];
}
}
private static final int[] DAY_OF_MONTH = {
31, 28, 31, 30, 31, 30,
31, 31, 30, 31, 30, 31
};
private static boolean isLeapYear(int year) {
if (year % 400 == 0) {
return true;
}
return year % 4 == 0 && year % 100 != 0;
}
private static boolean checkDay(int year, int month, int day) {
if (month != 2) {
int i = month - 1;
return day >= 1 && day <= DAY_OF_MONTH[i];
}
if (isLeapYear(year)) {
return day >= 1 && day <= 29;
}
return day >= 1 && day <= 28;
}
private static boolean checkMonth(int month) {
return month >= 1 && month <= 12;
}
private static boolean checkYear(int year) {
return year >= 1000 && year <= 3000;
}
}public class Time {
private int hour;
private int minute;
private int second;
public Time(int hour,int minute,int second){
if (!checkHour(hour)){
throw new RuntimeException("时应处于1-24");
}
if (!checkMinute(minute)){
throw new RuntimeException("分应处于1-60");
}
if (!checkSecond(second)){
throw new RuntimeException("秒应处于1-60");
}
this.hour=hour;
this.minute=minute;
this.second=second;
}
private static boolean checkSecond(int second) {
return second>=0&&second<60;
}
private static boolean checkMinute(int minute) {
return minute>=0&&minute<60;
}
private static boolean checkHour(int hour) {
return hour>=0&&hour<24;
}
public void fastForwardOnesecond(){
second++;
if (second==60){
minute++;
second=0;
}
if (minute==60){
hour++;
minute=0;
}
if (hour==24){
hour=0;
}
return;
}
public void stepBackforasecond(){
second--;
if (second<0){
minute--;
second=59;
}
if (minute<0){
hour--;
minute=59;
}
if (hour<0){
hour=23;
}
return;
}
public String toString(){
return String.format("%02d:%02d:%02d",hour,minute,second);
}
}
三、复杂度(complexity)
????????是一个评价程序(算法)好坏的标准
????????两个维度:
????????1.运行速度-时间复杂度(重心)
????????2.需求空间一空间复杂度
????????时间复杂度:
????????直接掐表的缺陷:影响因素太多,无法控制变量
????????所以,寻找其他替代方案
????????前提:给定CPU之后,单位时间内执行的指令条数基本是恒定
????????A算法解决问题需要50条指令
????????B算法解决问题需要500条指令
????????所以,衡量算法的运行时间被转换为衡量算法的执行指令个数
????????前提: Java 中的"基本语句0(1)"可以近似的看作指令的替代
????????即使固定算法,随着算法处理的数据规模的不同,算法需要的语句数也是不同的
????????所以:
????????我们希望得到的时间复杂度,是一个语句个数关于数据规模的函数关系
????????基本语句个数= f(数据规模)
????????例1:
????????指令个数=n*n+ 2*n +10
????????O(n* n)
????????例2:
????????指令个数=2*n + 10
????????O(n)
????????我们探讨的前提是n比较大, n趋于正无穷
大0标记
1)只保留函数关系中的最高次项
2)把保留的项的常数系数变成1
?
for (int i= 0;i < array.length- 1;i++){
//每次冒泡之前,有个乐观的假设,认为整个无序区间是有序的
boolean sorted = true
for (int j= 0;j < array.length-i- 1;j++){
if (array[j] > array[j + 1]) {
//只要冒泡过程中发生数据交换,意味着假设不成立
swap(array, i, j); .
sorted = false;
}
//一次冒泡结束,如果假设成立,不再需要以后的冒泡过程
}
if (sorted) { break; }
for (int i= 0;i< array.length - 1;i++){
//1.优化去掉
//2.数据规模.
array.length~ n
for (int j= 0;j< array.length-i-1;j++){
//3.函数关系
if (array[j] > array[j + 1]){
//f(n)= n*(n-1)/2
//4.大0表示法
swap(array, i, j);
O(n^2)
}
}
}
//二分查找的时间复杂度
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin)/2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end=mid-1;
//O(log(n))
}
return -1;
//0(1) < O(log(n)) < O(n) < O(n^2)
?假设在某台计算机上,冒泡排序50个数,耗费6秒的时间
请问,冒泡排序500个数,需要多少时间?
O(n^2)
n的规模扩大了10倍,消耗的时间10^2
600s
时间复杂度(Time Complexity):
估算算法执行时间和数据规模之间的变化关系
通过计算基本语句(O(1))的次数+大0渐进表示法+估算
1.找出最坏情况
2.确定数据规模的量
3.确定函数关系
4.大0渐进表示法: 1) 保留最高次项
2)系数变成1
常见的时间复杂度
0(1) < O(log(n)) < O(n) < O(n* log(n)) < O(n^2) | O(n^3) | O(2^n)
执行时间超时
空间复杂度(Space Complexity)粗略地认为是内存消耗的大小和数据规模的关系
1.算法的输入参数占用的空间,不计算在空间复杂度内
数组排序:传入数组占用的空间不算
?
int[] fibonacci(int n) {
1ong[] fibArray = new 1ong[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for(inti=2;i<=n;i++)
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fi bArray;
}
四、顺序表
?数据结构(Data Structure)
一门研究关于数据的组织结构管理的学科
逻辑层:线性结构(linear structure)
List
物理层:
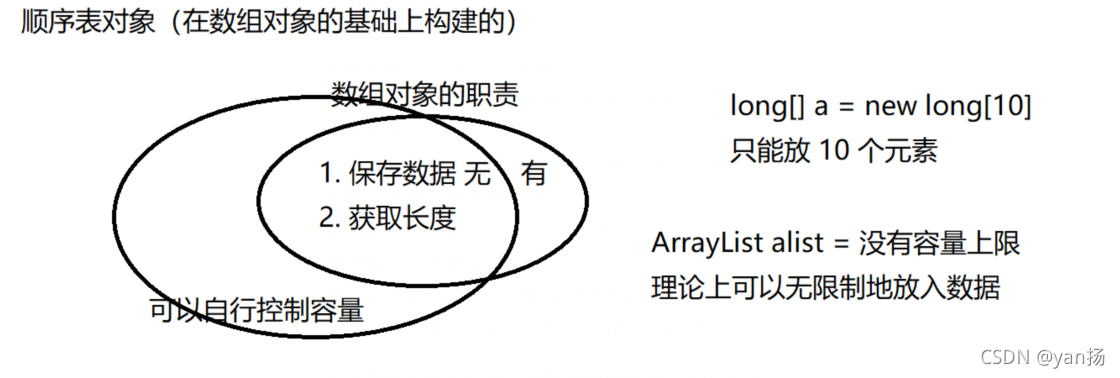
1)顺序结构(顺序表)
ArrayList
2)链式结构(链表)
LinkedList
线性结构
1.整体结构, - -般记为容器
2.装在容器中的单独的数据,称为元素(element)、 项 (item)
数据(data) 、值(value)
3.除了第一-个元素和最后- -个元素之外
所有剩余的元素都有共性
都有前一个元素(previous prev)
都有后一个元素(next)
第一个元素:没有prev,有next,记为first、head
最后一个元素:没有next,有prev,记为last、tail
4.只有在线性结构中,才有讨论第几个元素的条件
下标是表示第n个的代码表示,所有只有在线性结构中,下标才有意义
只有在线性结构中,才有顺序的含义(排序有意义)
5.数组也算一-种较 为特殊的线性结构
数组在保存元素时运行出现空洞
线性结构不允许
?

 ?
?
?
