目录
public class main {
public static void main(String[] args) {
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
}
}
1. 查看PriorityQueue

2. 找到new PriorityQueue, 也就是初始化的时候代码
public PriorityQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
发现使用的是 this, 查看 this
3. 查看 this
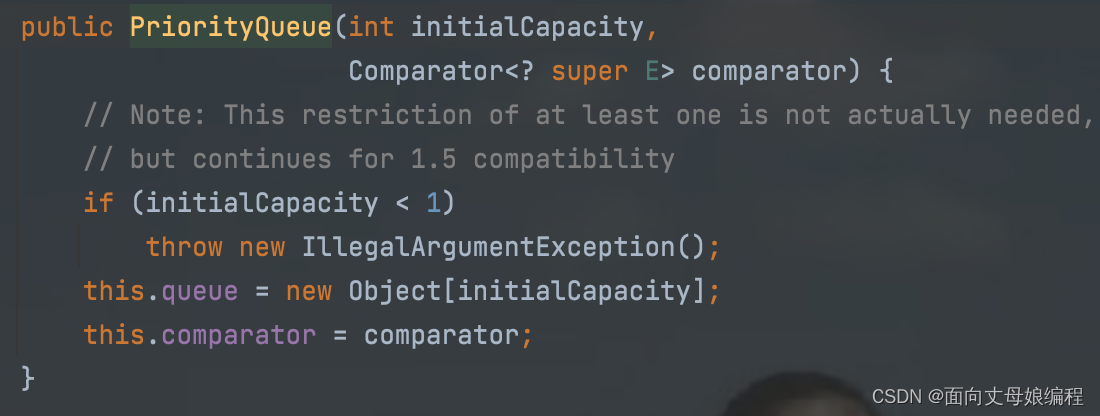
private static final int DEFAULT_INITIAL_CAPACITY = 11
所以 if 的代码块不会执行
this.queue 是 transient Object[] queue
this.comparator 是 传入的 null
到目前为止, 我们已经知道当我们 new 一个无参数的优先级队列的时候默认的容量为 11
那么问题来了: 既然是优先级队列, 那么到底是一个小堆还是大堆呢?
public class main {
public static void main(String[] args) {
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
minHeap.offer(0);
minHeap.offer(-1);
minHeap.offer(1);
System.out.println(minHeap.poll());
System.out.println(minHeap.poll());
System.out.println(minHeap.poll());
}
}
-1
0
1
4. 如何建立小根堆
4.1 offer分析
第一个弹出的元素就是最小值, 说明是一个小堆
如图所示
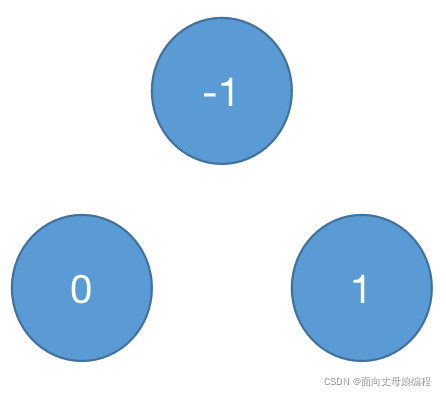
如过不熟悉堆, 可以查看我排序博客中堆排序对堆的详细介绍[由于是升序, 所以用的大根堆]
这里是小根堆
第一次 poll 之后的堆

现在弹出了元素, 就要对堆进行调整
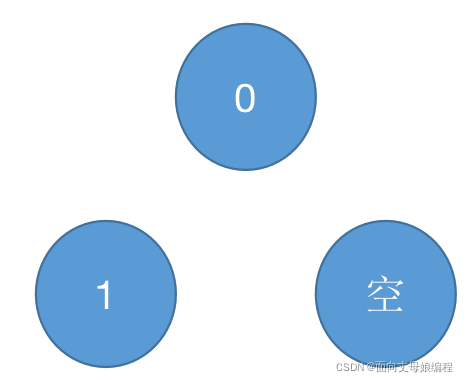
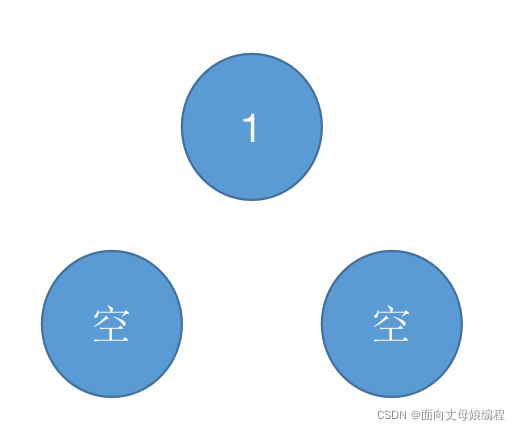
具体代码实现
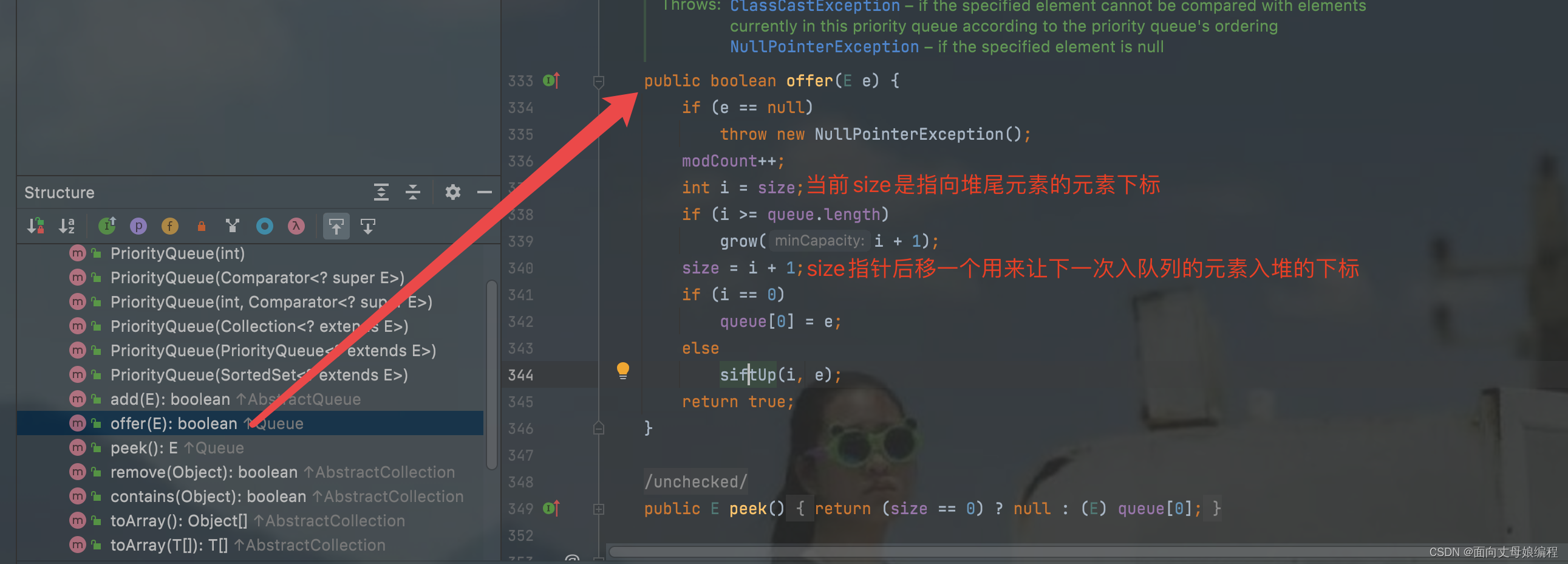
offer 函数【alt+7, 会在idea左边显示 PriorityQueue的所有方法】
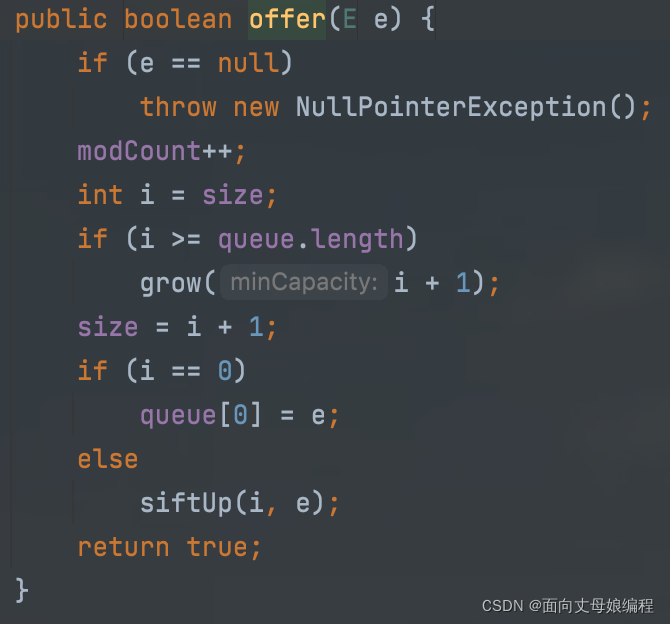
4.1.1 队列扩容
4.1.1.1 扩容实现
if (e == null)
为空就抛出空异常
int i = size;
if (i >= queue.length)
grow(i + 1);
size = i + 1;
还差1个元素满了就扩容
查看如何扩容
grow函数
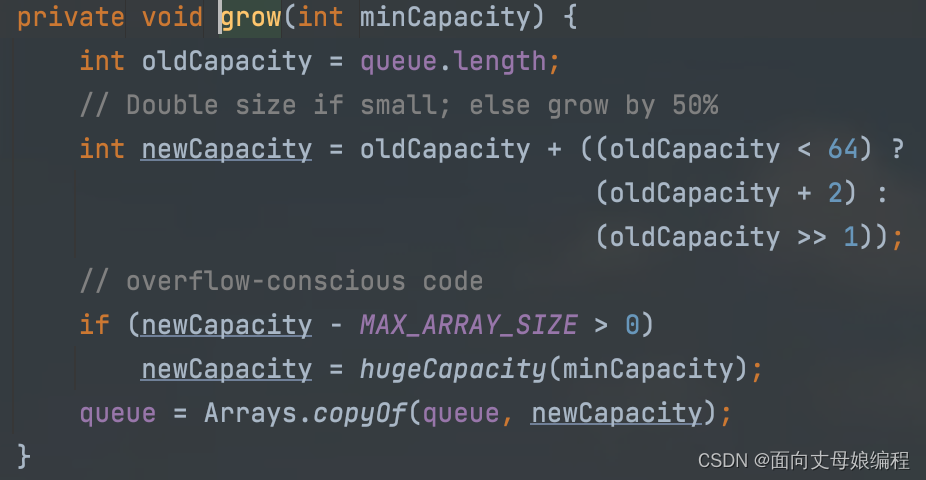
oldCapacity: 是代表当前队列的长度
newCapacity: 当前容量低于 64 的时候, 每次增加 2 个容量, 如果比 64 还大的话, 每次2个2个的增加会有多余开销【就相当于当有有1千的元素的时候每次扩容操作只增加2个容量, 虽然节约了空间但每次都插入数据的都需要扩容操作】这个时候会采用 2倍 扩容的方式进行扩容
4.1.1.2 考虑扩容溢出
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
当扩容后新的容量已经大于 MAX_ARRAY_SIZE【Integer的最大值减8】
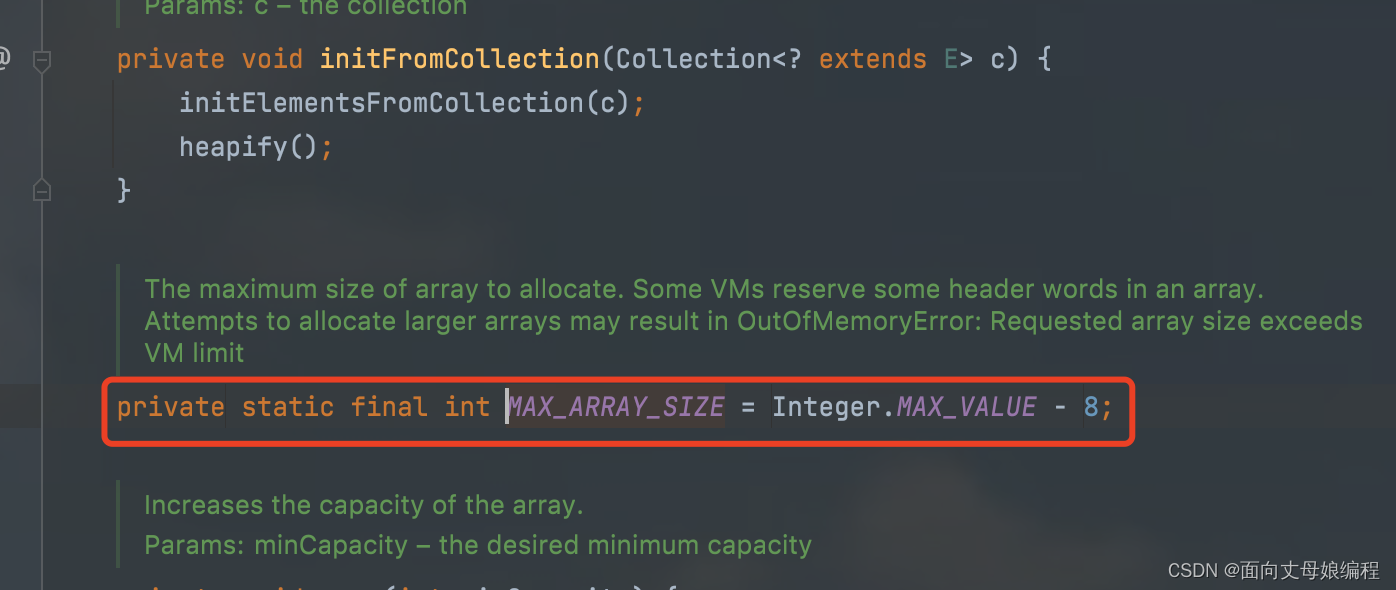
我们查看一下 private static int hugeCapacity(int minCapacity) 这个函数
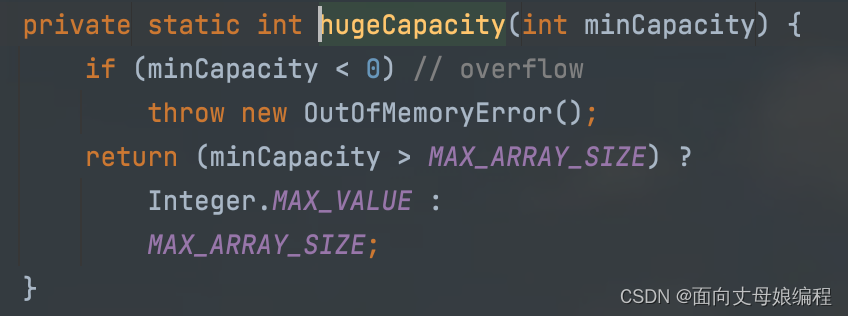
会发现, 如果达到了 Integer.MAX_VALUE最值之后, 返回的是 Integer.MAX_VALUE, 且无法继续扩容. 因此, JDK源码中的堆也并不是一直都能扩容的, 即使机器的内存很大也会被底层限制数据量大小
最后通过数组拷贝实现扩容操作
queue = Arrays.copyOf(queue, newCapacity);
4.1.2 调整为小根堆
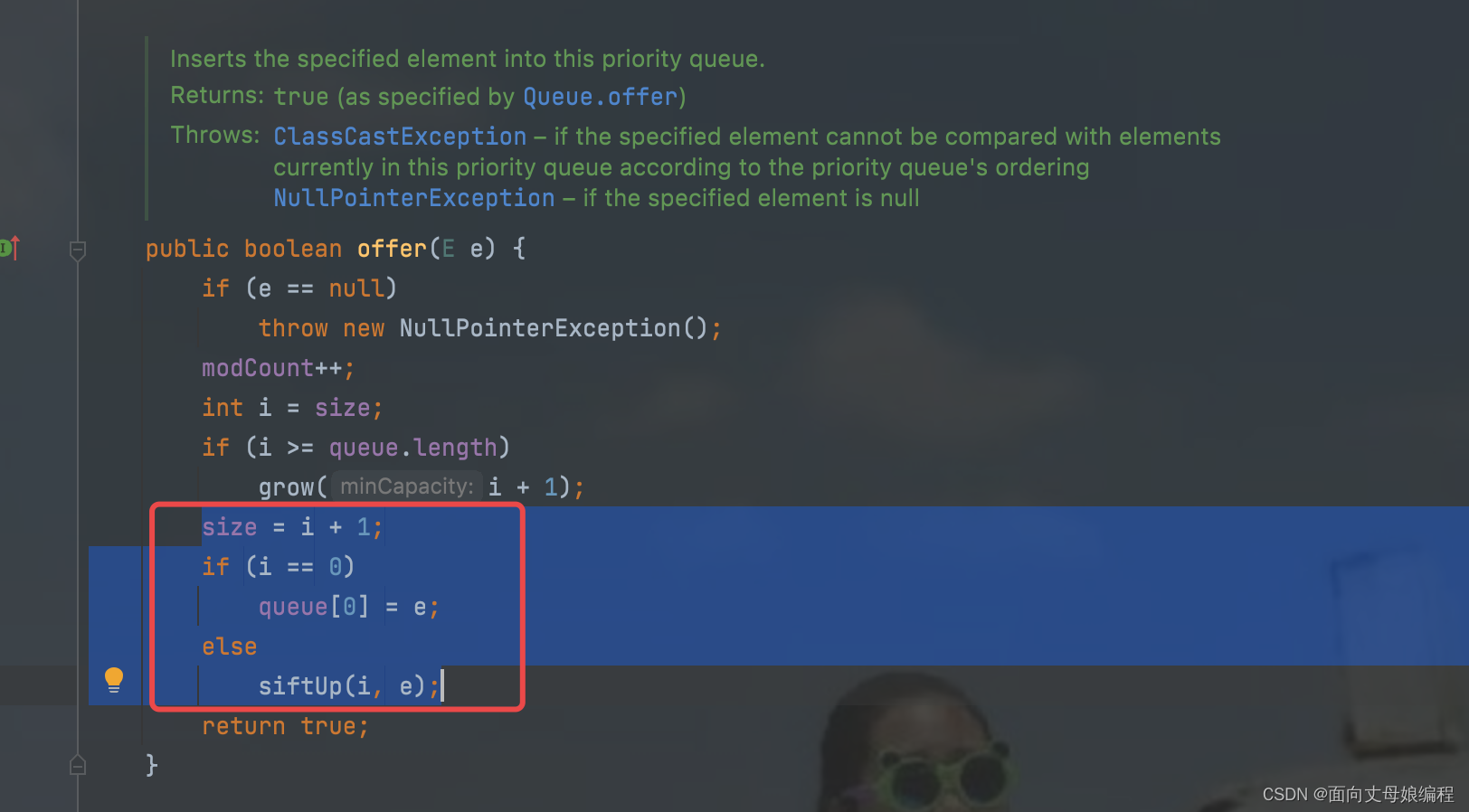
经历了扩容后就应该进行调整队列为小根堆【每添加一次就调整一次】
查看 siftUp(i, e) 源码
翻译
在位置k处插入项x,通过在树中向上提升X直到它更大来保持堆不变。
大于或等于其父对象,或者是根。来简化和加速胁迫和比较。这个。
可比较版本和比较器版本被分成不同的方法,否则。一模一样(SieftDown也是如此)。
参数:k代表堆的下标, 取值为堆的最后一个元素+1的下标也就是在堆的最后一个元素末尾插入一个新的元素 e
X: 要插入的值 e【这里的E是一个泛型】

是不是已经忘记了还有一个 comparator 的类常量?
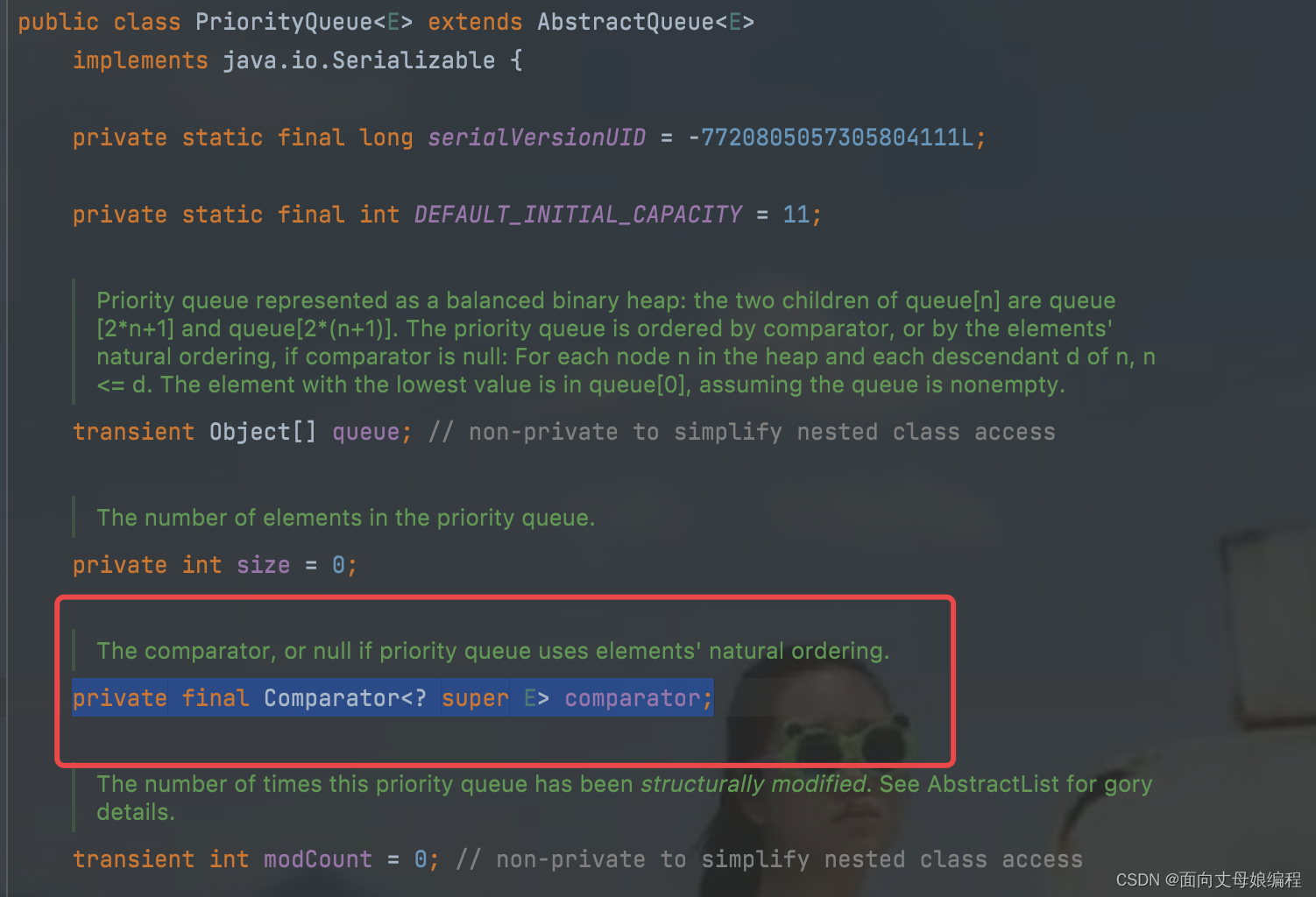
程序源码分析到这儿先透露一点 comparator 比较器是一个 null
原因是:
我们用的时候是用的无参构造的优先级队列

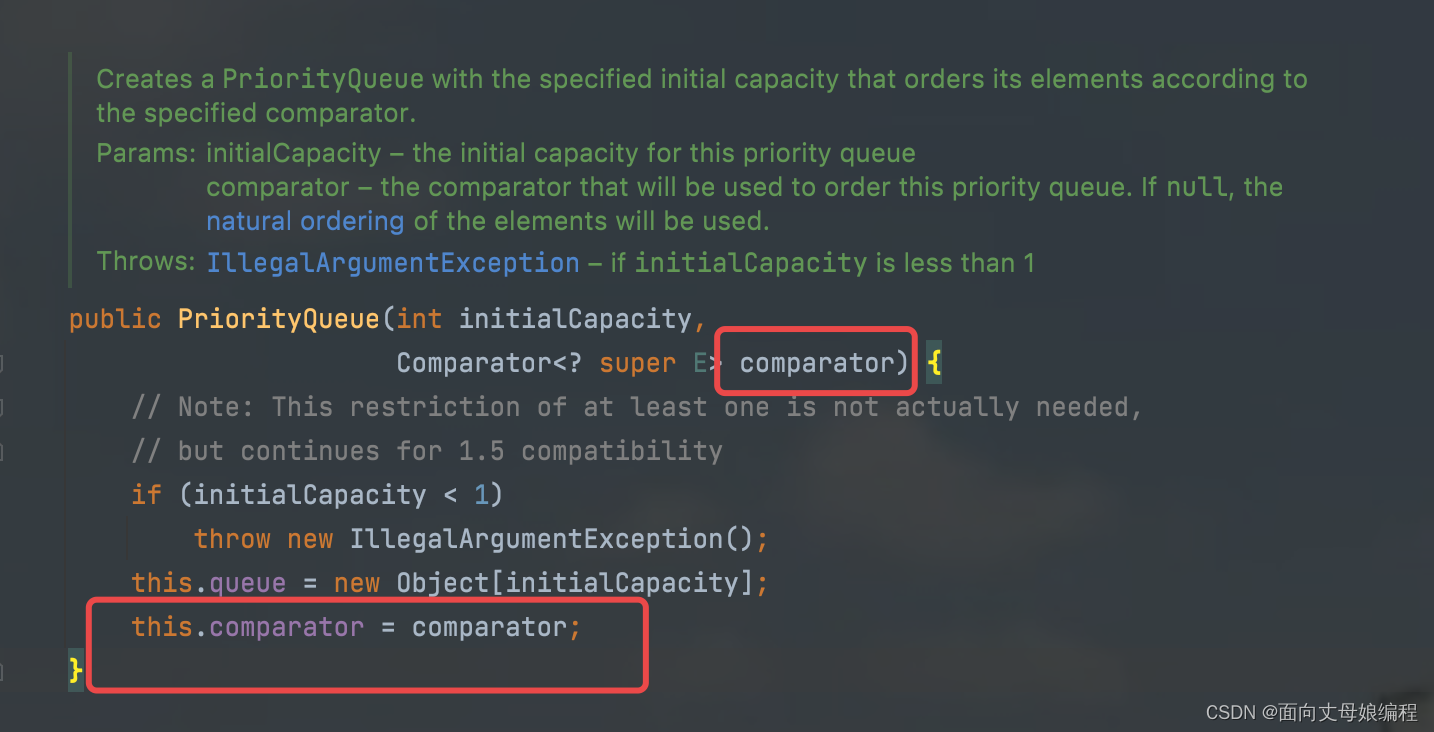
this代表当前类, this.comparator就代表的类中定义的那个常量比较器. 由于无参构造的优先级队列, 所以传入的形参 comparator 就是 null, 赋值给 this.compartor, 所以 this.comaprator也就是 null
因此会执行 else 的代码
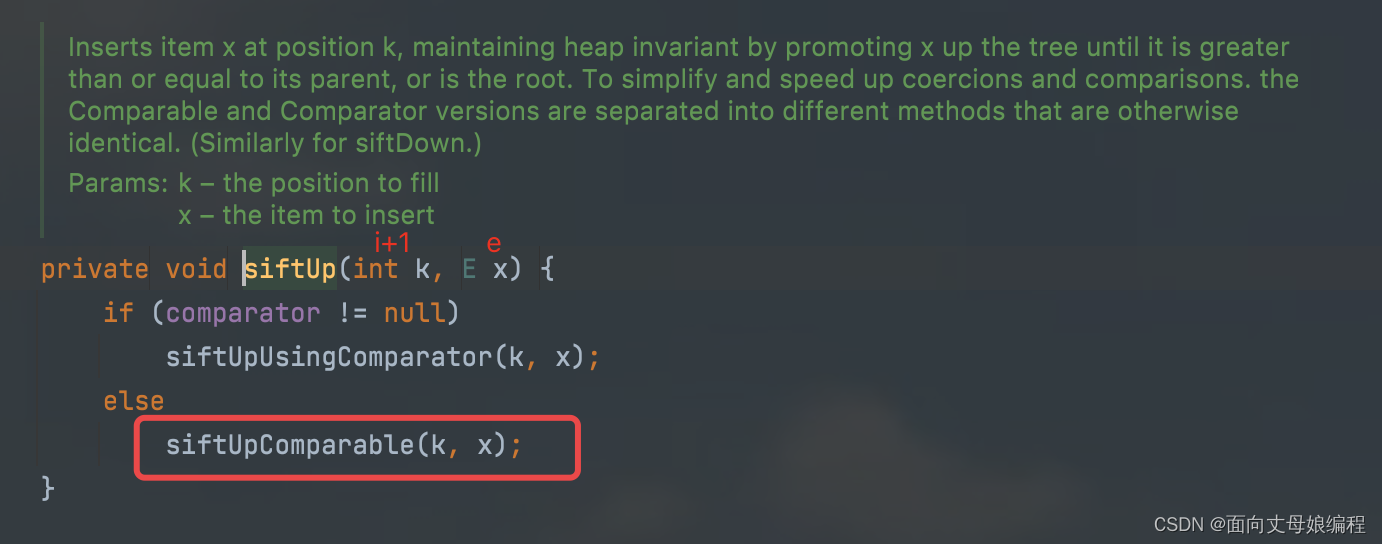
查看 private void siftUpComparable(int k, E x)
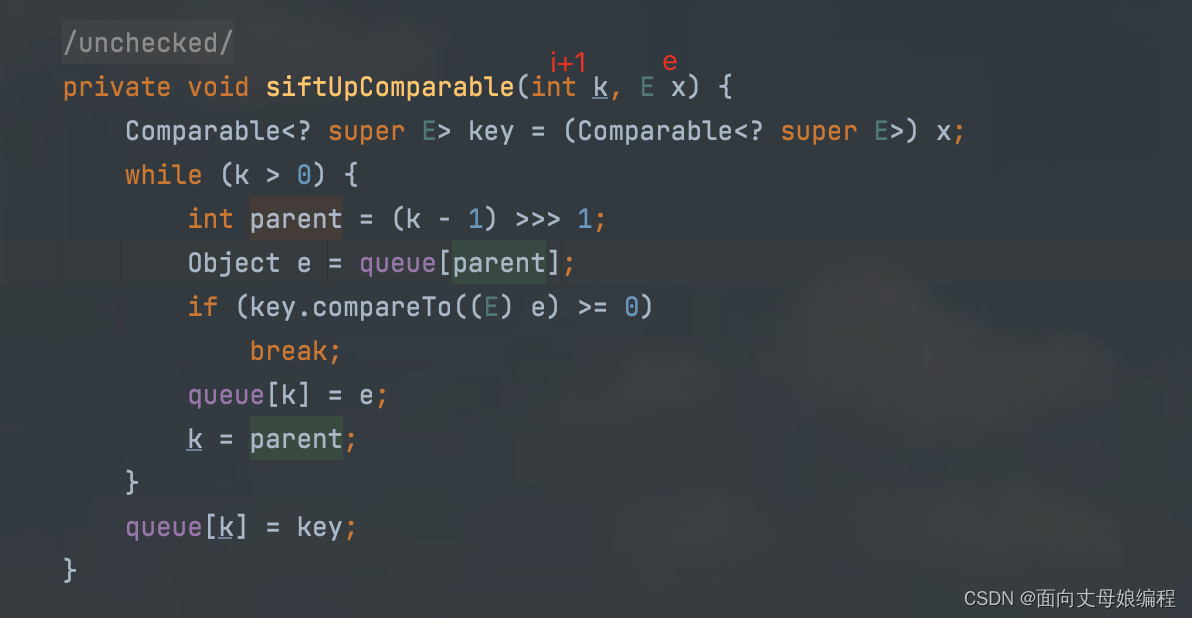
private void siftUpComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;// 首先将传入的范型参数 e 通过 Comparable 接口转变为可比较对象且这个对象的下界时不能低于泛型 e【也就是说这个 e 必须是 e类型的本身或者父类】
while (k > 0) {// 循环调次i+1节点上的所有父节点
int parent = (k - 1) >>> 1;// 通过孩子节点计算出父节点父节点=【孩子节点 - 1】/2
Object e = queue[parent];// queue 就是父类中定义的 transient Object[] queue. 此时选取的是父类的节点值
if (key.compareTo((E) e) >= 0)// 如果孩子的值比父类的值大就退出循环进行
break;
queue[k] = e;// 可以直接赋值因为k=i+1, 直接在最后一个元素的下一个下标赋值因此不会覆盖原数据
k = parent;// 更新孩子节点, 便于下次循环
}
queue[k] = key;// 循环结束, 此时如故是 k 为0, 则堆顶就直接赋值给 x, 此时x就是最小值; 如果是因为 break 推出循环, 则说明此时由于 k=i+1, 因此还是保持住了堆顶元素最小也就所谓的小根堆
}
4.2 poll分析
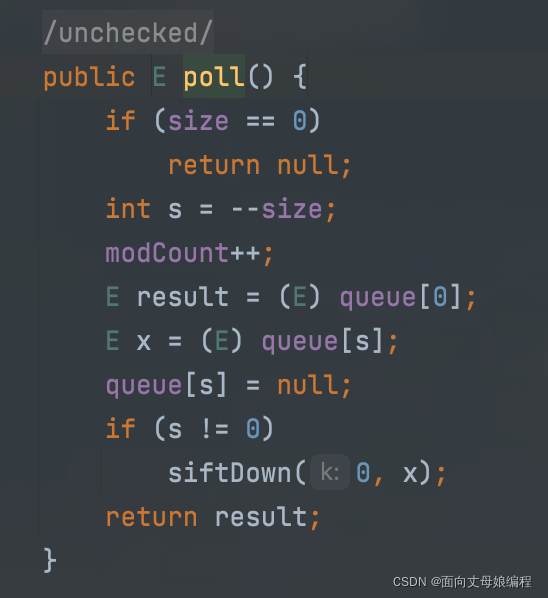
public E poll() {
if (size == 0)// 如果为空队列, 就返回 null
return null;
int s = --size;// 保存出队列之后当前队列中元素个数, 方便判断如果是最后一个元素的话就不进行堆的调整操作
modCount++;
E result = (E) queue[0];// 保存堆定值用于返回给调用者
E x = (E) queue[s];//保存堆最后一个元素的值
queue[s] = null;// 出队列一个之后, 释放堆中最后一个元素的内存空间
if (s != 0)// 如果出队列后队列中还有元素
siftDown(0, x);// 继续堆的调整, 保证堆是一个小根堆
return result;// 返回调用者
}
查看 private void siftDown(int k, E x) 函数
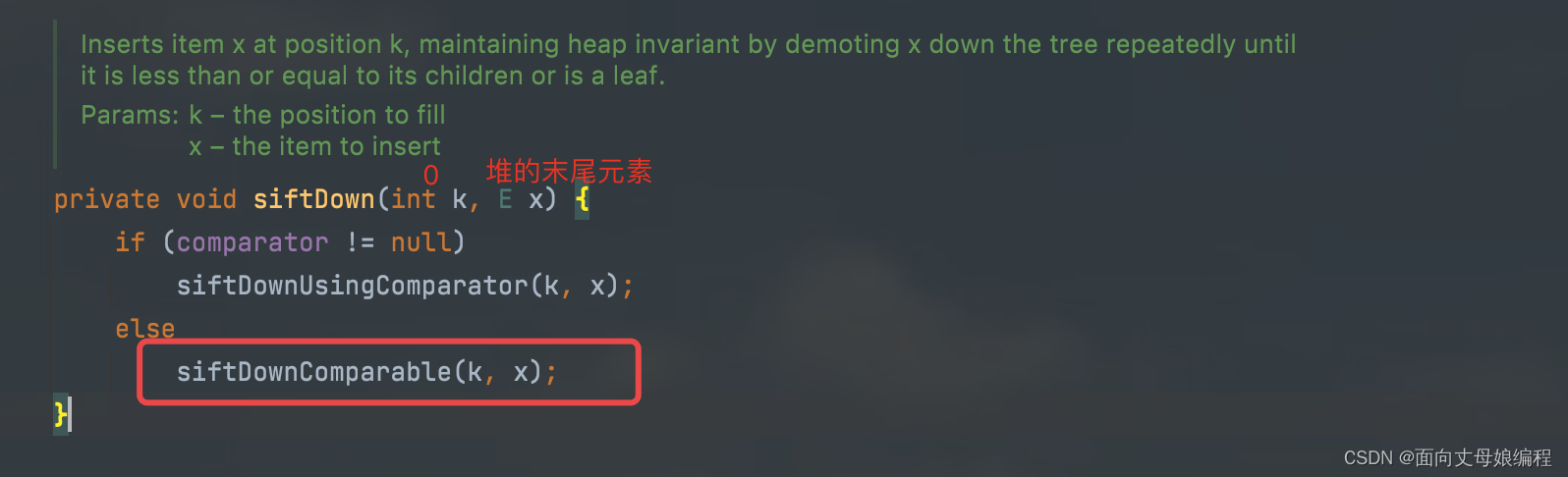
至此, 我们知道了会执行 else 而不是执行 if【当我们new 一个比较器的时候就会执行 if 中的代码块】
查看 private void siftDownComparable(int k, E x)
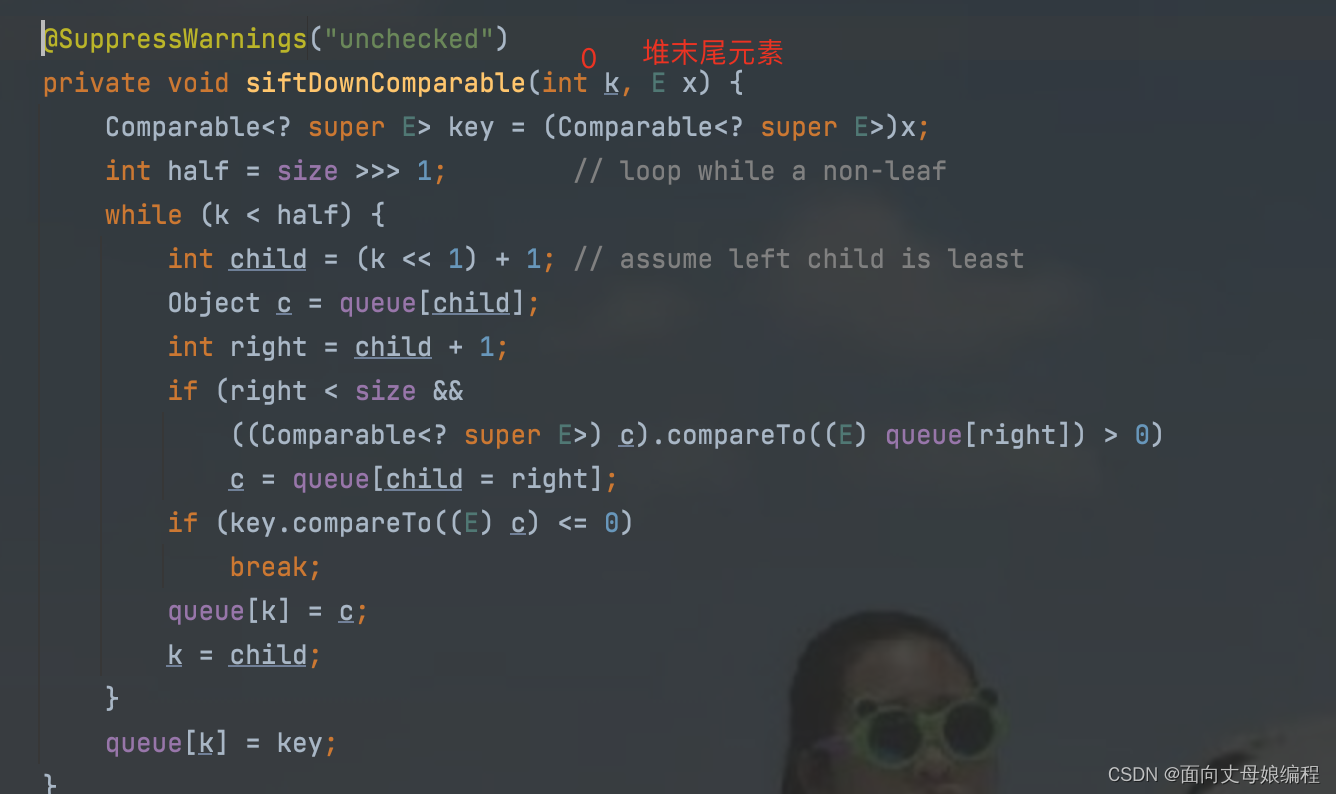
此时
poll的private void siftDownComparable(int k, E x)和offer的private void siftDownComparable(int k, E x)函数不一样, 发生了 重写
我们一步一步分析一下
@SuppressWarnings("unchecked")// 消除泛型的非受察警告, 这一点offer 中也有
private void siftDownComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>)x;// 和 offer 的一样, 将传入的堆尾参数强转为 Comparator 对象
int half = size >>> 1; // loop while a non-leaf: 无符号右移, half保持在队列的中间下标+1位置
// 下面的注释都是按照第一次循环
while (k < half) {// 从堆的1/2开始, 循环调整整个分之上的父节点使其上升, 处于堆定最小值【我们自己实现的小根堆一般是从堆底开始向上】
int child = (k << 1) + 1; // assume left child is least: 由于第一次 k 为 0, 所以 child 为 1【此时k为父节点下标, child为子节点下标】
Object c = queue[child];// 获取k的左子树【为了好理解, 可抽象为二叉树那样的数据结构】
int right = child + 1;// 计算k的右子树下标
if (right < size &&//保证右子树不越界
((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)// 并且左子树的值 > 右子树的值
c = queue[child = right];// 那么 k 的子节点就是左右子树的最大值
if (key.compareTo((E) c) <= 0)// 判断 堆尾元素key 和 最大子节点c 的大小关系
break;// 如果堆尾元素 小于等于 堆顶元素的最大子节点就退出循环
queue[k] = c;//程序执行到这儿, 说明堆顶元素就变为了了上一个堆定元素的左右子树中的最大值
k = child;//更新父节点, 使其带动循环调整
}
queue[k] = key;// 程序执行到这儿, 如果是因为break推出则说明堆尾元素 小于等于 堆顶元素的最大子节点, 则此时堆尾元素覆盖掉堆顶元素此时依旧保持了目前的小根堆性质; 如果是因为 while 循环到 k==half 而退出循环则此时就把堆顶元素用堆尾覆盖, 由于不是break推出循环, 所以每次堆顶元素都是前一个堆顶元素的左右子树最大值, 由于满足 if 条件【堆尾元素<=前一个堆顶元素的左右子树最大值】, 所以堆尾覆盖的时候依旧是一个小根堆
}
手动实现一个小根堆
import java.util.Arrays;
import java.util.PriorityQueue;
public class main {
private static void shiftUp(int[] arr, int child) {
int parent = (child - 1) >> 1;
while (parent >= 0) {
if (arr[child] > arr[parent]) {
swap(arr, child, parent);
child = parent;
parent = (child - 1) >> 1;
} else {
break;
}
}
}
private static void swap(int[] arr, int x, int y) {
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
private static void createMinHeap(int[] arr) {
for (int child = arr.length - 1; child >= 0; --child) {
shiftUp(arr, child);
}
}
public static void main(String[] args) {
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
int arr[] = {1, 3, 5, 7, 10, 9, 100, 2, 4, 6, 8,};
createMinHeap(arr);
System.out.println(Arrays.toString(arr));
}
}
数组中最大元素永远在堆顶也就是下标0处
[100, 10, 9, 7, 3, 1, 5, 2, 4, 6, 8]
5. Top-K问题
获取数组中前 K 个最大值
栗子:
int[] arr = {-1, -3, -5, -7, -9, -2, -4, -6, -8, -10};
我想获取前三个最大值, 该怎么办呢?
5.1 全排序
肯定会想到速度最快的 快排了, 时间复杂度为 O(logN)
这里已经有优化快排的性能
class sortAll {
int[] quickSort(int[] arr, int k) {
long before = System.currentTimeMillis();
quick(arr);
long last = System.currentTimeMillis();
int[] ret = new int[k];
System.out.print("前" + k + "个大的元素:");
for (int i = 0; i < k; i++) {
ret[i] = arr[arr.length - 1 - i];
System.out.print(ret[i] + " ");
}
System.out.println("快速排序全排列耗时:" + (last - before));
return ret;
}
private void quick(int[] arr) {
Stack<Integer> stack = new Stack<>();
stack.push(0);
stack.push(arr.length - 1);
while (!stack.empty()) {
int right = stack.pop();
int left = stack.pop();
int[] mid = partition(arr, left, right);
if (mid[0] - 1 > left) {
stack.push(left);
stack.push(mid[0] - 1);
}
if (mid[1] + 1 < right) {
stack.push(mid[1] + 1);
stack.push(right);
}
}
}
private int[] partition(int[] arr, int left, int right) {
int less = left - 1;
int more = right;
int cur = left;
while (cur < more) {
if (arr[cur] < arr[right]) {
swap(arr, cur++, ++less);
} else if (arr[cur] > arr[right]) {
swap(arr, cur, --more);
} else {
++cur;
}
}
swap(arr, more, right);
return new int[]{less + 1, more};
}
private void swap(int[] arr, int x, int y) {
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
}
5.2 部分排序
class sortPart {
int[] bubbleSort(int[] arr, int k) {
long before = System.currentTimeMillis();
for (int i = 0; i < k; i++) {
boolean flag = true;
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {//降序排列
swap(arr, j, j + 1);
flag = false;
}
}
if (flag) {
break;
}
}
int[] ret = new int[k];
System.out.print("前" + k + "个大的元素:");
for (int i = 0; i < k; i++) {
ret[i] = arr[arr.length - 1 - i];
System.out.print(ret[i] + " ");
}
long last = System.currentTimeMillis();
System.out.println("冒泡部分排序耗时: " + (last - before));
return ret;
}
private void swap(int[] arr, int x, int y) {
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
}
5.3 堆
排序升序建立大根堆, 因为数组元素比堆顶元素大就代表比其它元素大; 降序用小根堆, 数组元素比堆顶元素小, 一定比其它元素小
TopK最大值, 建立小堆, 只有把小根堆堆顶元素全部和数组元素比较替换完毕才能保证整个堆中是最大值
class heap {
int[] TopK(int[] arr, int k) {
long before = System.currentTimeMillis();
if (arr == null || arr.length == 0) {
return null;
} else {
// 1.优先级队列默认是建立小根堆
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
// 2.建立大小为 k 的堆
for (int e : arr) {
if (minHeap.size() < k) {
minHeap.offer(e);
} else {
int top = minHeap.peek();
if (e > top) {// 获取前 K 个大元素利用小根堆原理: 如果比堆中最小的大, 那一定比堆中其它元素大方可入堆. 如果用大根堆, 只能表明比堆顶最大元素大并不能保证比堆中其它元素的值大
minHeap.poll();
minHeap.offer(e);
}
}
}
System.out.print("前" + k + "个元素是:");
int[] ret = new int[k];
for (int i = 0; i < k; i++) {
ret[i] = minHeap.poll();
System.out.print(ret[i] + " ");
}
long last = System.currentTimeMillis();
System.out.println("堆解决耗时:" + (last - before));
return ret;
}
}
}
5.4 TopK问题不同方案的效率对比
import java.util.PriorityQueue;
import java.util.Stack;
// 随机产生1亿个数据来模拟海量数据的 TopK 情况下的性能
class createArr {
private int size = 1_0000_0000;
int[] arr;
createArr() {
this.arr = new int[size];
for (int i = 0; i < size; i++) {
arr[i] = (int) (size * Math.random());
}
}
}
class sortAll {
int[] quickSort(int[] arr, int k) {
long before = System.currentTimeMillis();
quick(arr);
long last = System.currentTimeMillis();
int[] ret = new int[k];
System.out.print("前" + k + "个大的元素:");
for (int i = 0; i < k; i++) {
ret[i] = arr[arr.length - 1 - i];
System.out.print(ret[i] + " ");
}
System.out.println("快速排序全排列耗时:" + (last - before));
return ret;
}
private void quick(int[] arr) {
Stack<Integer> stack = new Stack<>();
stack.push(0);
stack.push(arr.length - 1);
while (!stack.empty()) {
int right = stack.pop();
int left = stack.pop();
int[] mid = partition(arr, left, right);
if (mid[0] - 1 > left) {
stack.push(left);
stack.push(mid[0] - 1);
}
if (mid[1] + 1 < right) {
stack.push(mid[1] + 1);
stack.push(right);
}
}
}
private int[] partition(int[] arr, int left, int right) {
int less = left - 1;
int more = right;
int cur = left;
while (cur < more) {
if (arr[cur] < arr[right]) {
swap(arr, cur++, ++less);
} else if (arr[cur] > arr[right]) {
swap(arr, cur, --more);
} else {
++cur;
}
}
swap(arr, more, right);
return new int[]{less + 1, more};
}
private void swap(int[] arr, int x, int y) {
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
}
class sortPart {
int[] bubbleSort(int[] arr, int k) {
long before = System.currentTimeMillis();
for (int i = 0; i < k; i++) {
boolean flag = true;
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {//降序排列
swap(arr, j, j + 1);
flag = false;
}
}
if (flag) {
break;
}
}
int[] ret = new int[k];
System.out.print("前" + k + "个大的元素:");
for (int i = 0; i < k; i++) {
ret[i] = arr[arr.length - 1 - i];
System.out.print(ret[i] + " ");
}
long last = System.currentTimeMillis();
System.out.println("冒泡部分排序耗时: " + (last - before));
return ret;
}
private void swap(int[] arr, int x, int y) {
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
}
class heap {
int[] TopK(int[] arr, int k) {
long before = System.currentTimeMillis();
if (arr == null || arr.length == 0) {
return null;
} else {
// 1.优先级队列默认是建立小根堆
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
// 2.建立大小为 k 的堆
for (int e : arr) {
if (minHeap.size() < k) {
minHeap.offer(e);
} else {
int top = minHeap.peek();
if (e > top) {// 获取前 K 个大元素利用小根堆原理: 如果比堆中最小的大, 那一定比堆中其它元素大方可入堆. 如果用大根堆, 只能表明比堆顶最大元素大并不能保证比堆中其它元素的值大
minHeap.poll();
minHeap.offer(e);
}
}
}
System.out.print("前" + k + "个大元素是:");
int[] ret = new int[k];
for (int i = 0; i < k; i++) {
ret[i] = minHeap.poll();
System.out.print(ret[i] + " ");
}
long last = System.currentTimeMillis();
System.out.println("堆解决耗时:" + (last - before));
return ret;
}
}
}
public class main {
private static void testSortAll(int k) {
int[] createArr = new createArr().arr;
new sortAll().quickSort(createArr, k);
}
private static void testSortPart(int k) {
int[] createArr = new createArr().arr;
new sortPart().bubbleSort(createArr, k);
}
private static void testheap(int k) {
int[] createArr = new createArr().arr;
new heap().TopK(createArr, k);
}
public static void main(String[] args) {
int k = 4;
testSortAll(k);
testSortPart(k);
testheap(k);
}
}
前4个大的元素:99999999 99999998 99999997 99999995 快速排序全排列耗时:31671
前4个大的元素:99999999 99999998 99999998 99999998 冒泡部分排序耗时: 1132
前4个大元素是:99999996 99999997 99999999 99999999 堆解决耗时:228
意外的发现冒泡排序并非一无是处的, 某些情况下还是优于快速排序的. 但还是没有TopK解决速度快
现在已经知道了最基础的 TopK 问题
再分析两个具有代表性的 TopK 中等难度的问题
5.5 查找和最小的K对数字
力扣
找最小值, 则应该考虑建立大根堆, 因为如果比大根堆的堆顶元素还要小则说明此元素一定小于堆中其它元素的值
class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
// 1.重写 compare方法建立大根堆
PriorityQueue<List<Integer>> maxHeap = new PriorityQueue<>(new Comparator<List<Integer>>(){
@Override
public int compare(List<Integer> o1, List<Integer>o2){
return (o2.get(0)+o2.get(1))-(o1.get(0)+o1.get(1));
}
});
// 2.遍历两个数组
List<Integer> list = null;
for(int i=0; i<Math.min(k, nums1.length); ++i){
for(int j=0; j<Math.min(k, nums2.length); ++j){
// 3.堆没放满就添加
if(maxHeap.size()<k){
list = new ArrayList();
list.add(nums1[i]);
list.add(nums2[j]);
maxHeap.add(list);
}else{
// 4.放满后就和堆顶元素比较后小的再入堆
int top = maxHeap.peek().get(0) + maxHeap.peek().get(1);
if(top > nums1[i]+nums2[j]){
maxHeap.poll();
list = new ArrayList();
list.add(nums1[i]);
list.add(nums2[j]);
maxHeap.add(list);
}
}
}
}
List<List<Integer>> ret = new ArrayList<>();
for(int i=0; i<k && !maxHeap.isEmpty(); ++i){
ret.add(maxHeap.poll());
}
return ret;
}
}
为何o2-o1就是大根堆呢?
继续查看源码
我们找到传入比较器的参数的源码, 它会跳转到
public PriorityQueue(Comparator<? super E> comparator) {
this(DEFAULT_INITIAL_CAPACITY, comparator);
}
初始化容量为 11
再点击 this 跳转到如下函数

随意的查看 poll 或者 offer 的代码, 就可以查看到 shiftDown
由于size 初始化为 0【为了方便以下代码都按照第一次offer元素建堆来分析】
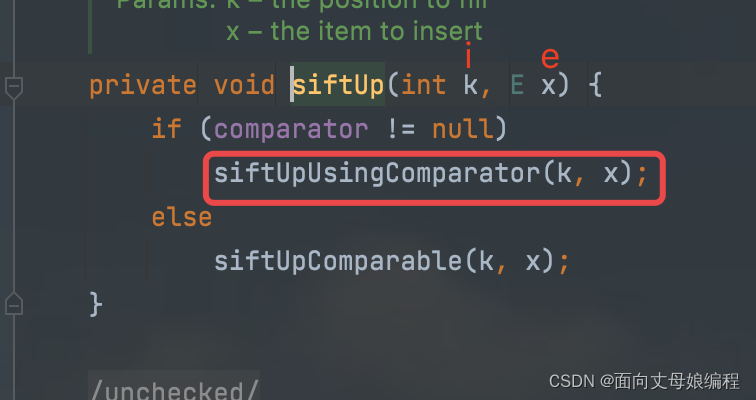
由于比较器不为空, 所以会按照规定的比较器而不是默认的比较器进行建堆
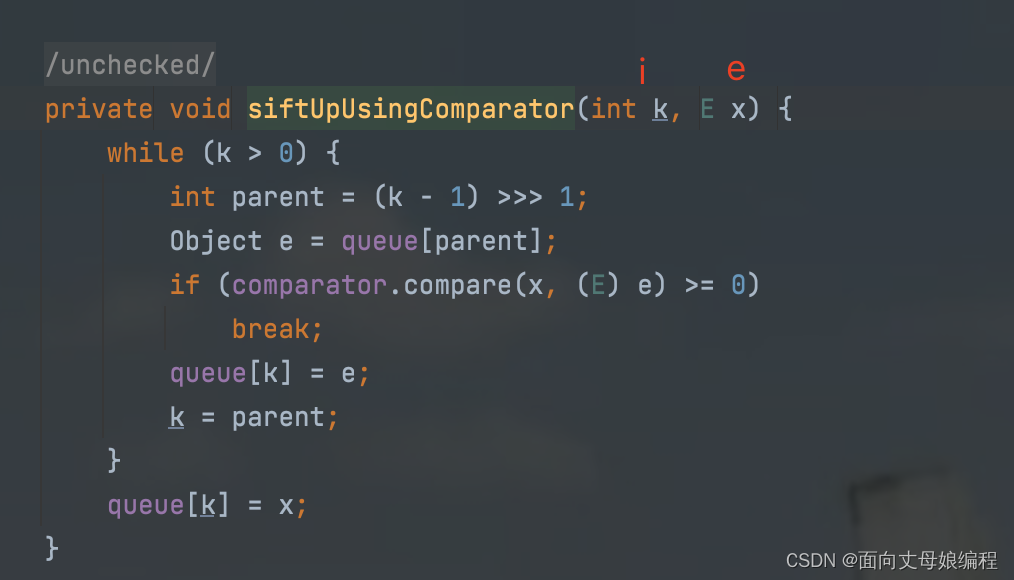
此时就很简单了
1 private void siftUpUsingComparator(int k, E x) {
2 while (k > 0) {
3 int parent = (k - 1) >>> 1;
4 Object e = queue[parent];
5 if (comparator.compare(x, (E) e) >= 0)
6 break;
7 queue[k] = e;
8 k = parent;
9 }
10 queue[k] = x;
}
Object e = queue[parent];
e代表的是形参x节点的父节点
图片中标注的 红色e 只是前一个函数
shiftUp(k, e)中的e, 并非下标 k 节点的父节点的 e
if (comparator.compare(x, (E) e) >= 0)
break;
这段代码是决定大小堆的核心代码
再看看我们的Comparable接口是如何实现的
public int compare(List<Integer> o1, List<Integer>o2){
return (o2.get(0)+o2.get(1))-(o1.get(0)+o1.get(1));
}
x 是 compare 的第一个参数也就是 o1
父节点 e 是 compare 的第二个参数也就是 o2
如果 x > e 就 break
如图所示
k=1
x对应形参中的x
e对应函数中 parent节点
我们在看 return 的代码是
o2-o1
如果父节点 e 比子节点 x 要大, 就不调整, 继续保持父节点的大根堆性质.
然后再看代码
7 queue[k] = e;
8 k = parent;
程序执行到这儿, 说明 x 是小于 父节点 e 的.
需要进行调整后再更新parent值使其循环处理这个分之上的每一个父节点一直到堆顶节点结束
queue[1] = e
k=0;
已经可以结束循环, 这里为了方便理解和解释顾只选取了两个元素进行说明

10 queue[k] = x;
程序执行到这儿, 说明已经完毕了, 最后赋值给堆顶元素
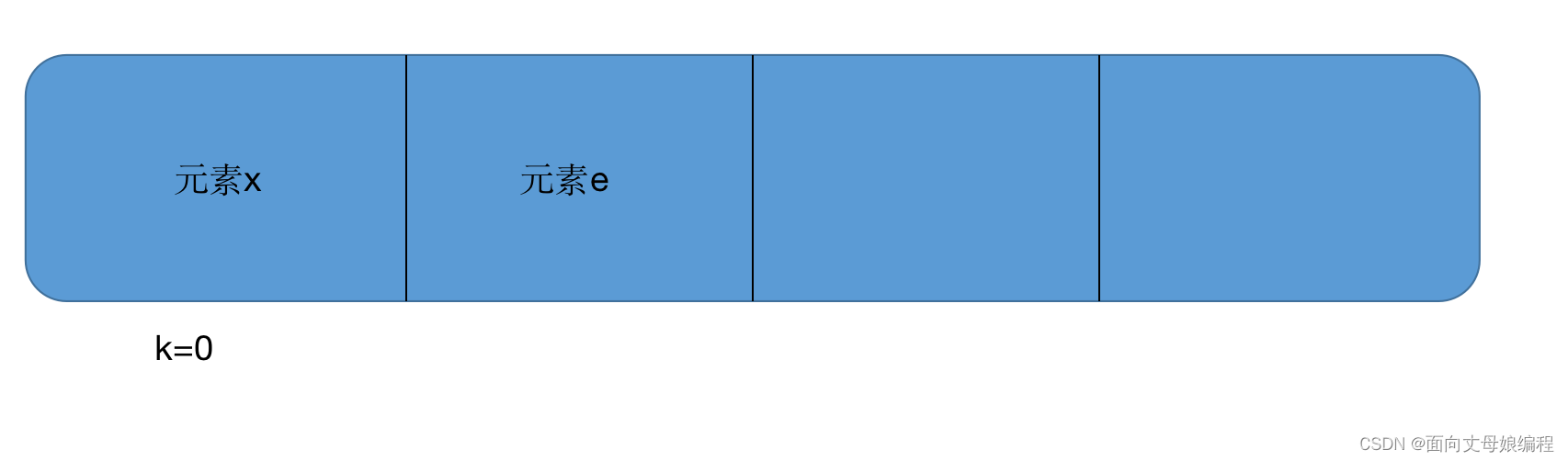
自此, 堆已经调整完毕.
5.6 前K个高频单词
首先应该考虑的是建立大小堆问题.
找到前 k 个高频单词, 也就是找到频率的最大值, 找最大值就建立小堆
可以使用全排序后截取来解决 TopK 问题
class Solution {
public List<String> topKFrequent(String[] words, int k) {
// 1.存放单词出现次数
HashMap<String, Integer> minHeap = new HashMap<>();
for(String x : words){
minHeap.put(x, minHeap.getOrDefault(x, 0) + 1);
}
// 2.存储所有的 key
List<String> wordList = new ArrayList<>(minHeap.keySet());
Collections.sort(wordList, new Comparator<String>(){
@Override
public int compare(String o1, String o2){
Integer count1 = minHeap.get(o1);
Integer count2 = minHeap.get(o2);
// 频率相同返回字母顺序
if(count1.equals(count2)){
return o1.compareTo(o2);
}else{
return count2-count1;
}
}
});
return wordList.subList(0, k);
}
}
这样就完成了 TopK 问题明显不可以, 我们来点也可以使用 TopK 的解法
class Solution {
public List<String> topKFrequent(String[] words, int k) {
// 1.存储所有的映射关系
HashMap<String, Integer> map = new HashMap<>();
for (String x : words) {
map.put(x, map.getOrDefault(x, 0) + 1);
}
// 2.建立小根堆
PriorityQueue<Map.Entry<String, Integer>> minHeap = new PriorityQueue<>(new Comparator<Map.Entry<String, Integer>>() {
@Override
public int compare(Map.Entry<String, Integer> o1, Map.Entry<String, Integer> o2) {
if (o1.getValue().equals(o2.getValue())) {
return o2.getKey().compareTo(o1.getKey());// 这里是这个题目的困难所在: 当频率相同的时候我们考虑的是字母顺序, 应为会被 Collections 反转所以就建立对同频率的大根堆, 即可 "反转" 经历 Collections 反转后就回归到正常顺序
} else {
return o1.getValue() - o2.getValue();// 按照顺序建立小根堆
}
}
});
// 3. 开始遍历, 拿到每一个 key-value 集合
for(Map.Entry<String, Integer> entry : map.entrySet()){
if(minHeap.size()<k){
minHeap.offer(entry);
}else{
// 3. 频率和字母两种情况讨论
Map.Entry<String, Integer> top = minHeap.peek();
if(entry.getValue().compareTo(top.getValue())==0){// 与堆顶元素频率相等
if(entry.getKey().compareTo(top.getKey())<0){// 与堆顶元素字母顺序: 小的入堆
minHeap.poll();
minHeap.offer(entry);
}
}else{// 频率不同
if(entry.getValue().compareTo(top.getValue()) > 0){// 频率高的入堆
minHeap.poll();
minHeap.offer(entry);
}
}
}
}
List<String> ret = new ArrayList<String>();
for(int i=0; i<k; ++i){
ret.add(minHeap.poll().getKey());
}
Collections.reverse(ret);// 反转一下
return ret;
}
}