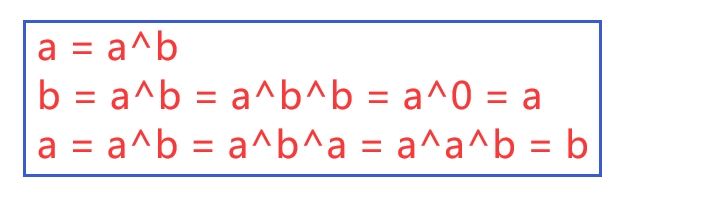位运算可以大幅度提高代码的运行效率,是每个人都应熟练掌握的解题技巧,首先感谢英雄大佬的b站视频,感兴趣的话可以前往b站一睹为快:可能会占据你陪女朋友的时间,但是你要相信……
位运算两大类:
逻辑位运算符
位移运算符
逻辑位运算符包括:
逻辑与(&&):只有两个运算数都为true是才是true,其他则为false。
逻辑或(||):如果其中一个或两个运算数都是true,那么返回true,如果两个运算数都是false,那么返回false。
位移运算符包括:
位与运算符(&):只有对应的两个二进位均为1时,结果位才为1 ,否则为0。
位或运算符(|):只要对应的两个二进位有一个为1时,结果位就为1。
异或运算符(^):只有对应的两个二进制位相同的时候,结果位返回0,否则返回1。
按位取反运算符(~):转换为二进制数后,0变1,1变0。
左移运算符(<<):把位按指定的值向左移动对应的位数,超过的位将丢失,空位补0,左移也可以看作是对此数乘以2。
右移运算符(>>):把位按指定的值向右移动对应的位数,移动过程中,正数最高位补0,负数最高位补1,右移也可以看作是对此数除以2。
举一些栗子:
1.231. 2 的幂


分析:当这个是小于或者等于0的时候,一定不是2的幂,我们可以知道二进制最高位为 1,其余所有位均为 0。所以这个数如果是2的幂,一定是1加上若干个0,那么我们减去一,也就是0加上若干个1,我们让这两个数进行位与运算,那么一定是若干个0。也就是我们有:n & (n - 1) == 0,所以此题可解。
class Solution {
public boolean isPowerOfTwo(int n) {
return (n > 0) && ((n-1) & n)==0;
}
}
2.342. 4的幂

分析:4的幂一定是2的幂,但是2的幂不一定是4的幂。我们可以推出,2的偶数次幂模3等于1,2的奇数次幂模3等于2。而2的偶数次幂正好是4的幂,所以我们可以知道,如果一个数字是2的幂,并且它模3等于1,那么它一定就是4的幂。
class Solution {
public boolean isPowerOfFour(int n) {
return (n > 0) && (n & (n - 1))== 0 && (n % 3 == 1);
}
}
分析:我们把一个数a的二进制数假设为(…1000),那么我们剪去1,就可以得到了(…0111),我们让(…1000)&(…0111),那么就可以得到(…0000),于是我们这样就可以把a的二进制数最低位的1消去了。我们通过这种操作,就可以把所有的1都消去了,然后统计消去的1的个数,我们就可以得到结果了。
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int number = 0;//记录1的个数
while(n!=0){
n &= (n - 1);
++number;
}
return number;
}
}
分析:我们先看一个运算规则,规则:0^0=0; 0^1=1; 1^0=1; 1^1=0;所以我们可以得到两个相同的数进行异或运算,可以得到0,那么一个数和0进行异或运算,就是得到这个数的本身。我们看下面这张图,这样就可以将a与b进行交换了:
class Solution {
public int[] swapNumbers(int[] numbers) {
numbers[0] = numbers[0]^numbers[1];
numbers[1] = numbers[0]^numbers[1];
numbers[0] = numbers[0]^numbers[1];
return numbers;
}
}
分析:我们先看一个运算规则,规则:0^0=0; 0^1=1; 1^0=1; 1^1=0;所以我们可以得到两个相同的数进行异或运算,可以得到0,那么一个数和0进行异或运算,就是得到这个数的本身。那么我们只要不断异或下去,就可以得到把出现两次的数全部解决,所以就可以剩下只出现了一次的数字。
class Solution {
public int singleNumber(int[] nums) {
int number = 0;
for(int i = 0; i < nums.length; i++){
number = number^nums[i];
}
return number;
}
}
分析:由下图可知,异或完去求所得结果上1的个数就是所求的汉明距离。
class Solution {
public int hammingDistance(int x, int y) {
int n = x^y;
int number = 0;
while(n != 0){
n &= (n - 1);
number++;
}
return number;
}
}
分析:我们对这个正整数的二进制进行两位两位判断,从尾部开始,向头部两位两位判断,如果相邻的这两个数是11或者是00,那么就不符合题意。我们又可以知道,二进制的00对应十进制就是0,二进制的11对应十进制就是3,于是我们可以让3的二进制不断与这个数的二进制数进行&运算,我们看一张图:
class Solution {
public boolean hasAlternatingBits(int n) {
while(n!=0){
if( (n & 3)==3 || (n & 3) == 0 ){
return false;
}
n>>=1;
}
return true;
}
}
分析:我们给定一个数组,将里面的子集进行分解:
如果二进制对应的位置上有1,就证明在集合里面,否则就不在。
上面的意思是,在i这个数的二进制表示中,从低到高第 j 位是否是1,把 1 的数字对应的位都进行异或,得到的结果累加到最终结果就是答案。
class Solution {
public int subsetXORSum(int[] nums) {
int answer,sum = 0;
for(int i = 0; i < (1<<nums.length); i++){
answer = 0;
for(int j = 0; j < nums.length; j++){
if((i&(1<<j))!=0){
answer^=nums[j];
}
}
sum = sum + answer;
}
return sum;
}
}
分析:首先我们可以看一下十进制的情况: 9+3=12,
第一步:相加各位的值,但是不算进位,得到2。
第二步:计算进位值,得到10。
第三步:重复上述两步,得到相加值为12。
¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥
我们可以同理计算二进制值相加: 比如101和111
第一步:相加各位的值,但是不算进位,得到010,二进制的每位相加就相当于各位做异或操作,101^111。
第二步:计算进位值,得到1010,相当于各位进行与操作得到101,再向左移一位得到1010,(101&111)<<1。
第三步:重复上述两步,各位相加 010^1010=1000,进位值为100=(010 & 1010)<<1。
继续重复上述两步:1000^100 = 1100,进位值为0,此时我们跳出循环,1100为最终结果。当我们的进位为0,即为最终所求结果。
class Solution {
public int getSum(int a, int b) {
return b == 0 ? a : getSum(a^b,(a&b) << 1);
}
}
分析:先把N的第i到第j都归零,然后把M插入到N的对应位置,归零可以使用位与&运算,将其和第k位为0,其余位为1的二进制数进行运算,达到消零操作:
然后我们在将N左移i位,和现在的数进行位或,就可以得到结果:
class Solution {
public int insertBits(int N, int M, int i, int j) {
for(int k = i; k <= j; k++){
N &= ~((long)1<<k);
}
return N|(M<<i);
}
}
学习位运算最好的时间是在大一,其次就是现在。