试题 A: 解密
小明设计了一种文章加密的方法:对于每个字母 c,将它变成某个另外的字符 T c 。下表给出了字符变换的规则:
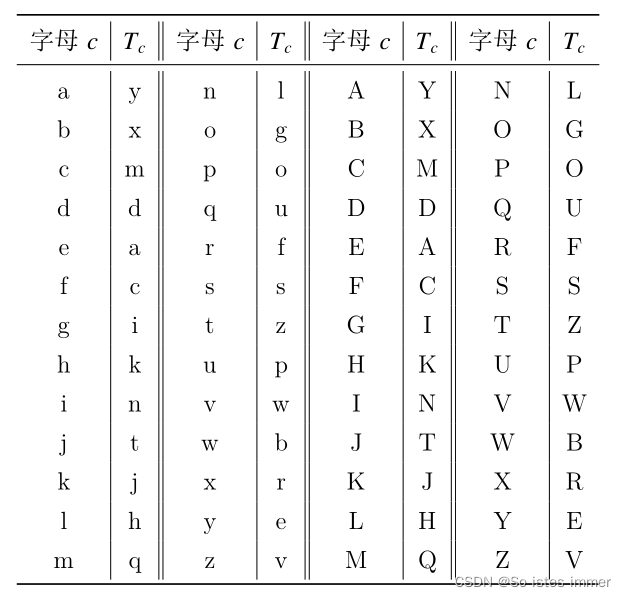
例如,将字符串 YeRi 加密可得字符串 EaFn。小明有一个随机的字符串,加密后为EaFnjISplhFviDhwFbEjRjfIBBkRyY(由 30 个大小写英文字母组成,不包含换行符),请问原字符串是多少?
答案:YeRikGSunlRzgDlvRwYkXkrGWWhXaA
试题 B: 纪念日
2020 年 7 月 1 日是CPC成立 99 周年纪念日。CPC成立于 1921 年 7 月 23 日。
请问从 1921 年 7 月 23 日中午 12 时到 2020 年 7 月 1 日中午 12 时一共包含多少分钟??
答案:52038720
闰年:24个? 平年:75个
(25*366+74*365)*24*60 - 22*24*60 =?52038720
试题 C: 合并检测

答案:10
分析:假设A国有n个人,感染者有n/100,每k个人一组,共n/k组,共用n/k瓶试剂
按照最坏的情况,每多出一个感染者就多用k瓶试剂,因此共用n/k+(n/100)*k瓶试剂
n=10时,n*(1/k+k/100)最小
试题 D: 分配口罩
某市市长获得了若干批口罩,每一批口罩的数目如下:(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 mask.txt,内容与下面的文本相同)
9090400
8499400
5926800
8547000
4958200
4422600
5751200
4175600
6309600
5865200
6604400
4635000
10663400
8087200
4554000
现在市长要把口罩分配给市内的 2 所医院。由于物流限制,每一批口罩只能全部分配给其中一家医院。市长希望 2 所医院获得的口罩总数之差越小越好。请你计算这个差最小是多少?
答案:2400
设这些数的和为sum,分为两组后,一组数的和必定<=sum/2,另一组数的和必定>=sum/2。
我们只需要求出这样一组数,它们的和<=sum/2,并且这个和要尽可能最大。
用dp[j]表示一组数的和,这个和<=j,并且在所有情况下最大,这里我们要求dp[sum/2]。
public class Main {
public static void main(String[] args) {
int[] nums = {9090400,8499400,5926800,8547000,4958200,4422600,5751200,4175600
,6309600,5865200,6604400,4635000,10663400,8087200,4554000};
int sum = 0;
for(int i = 0; i < nums.length; ++i) {
sum+=nums[i];
}
int half_sum = sum/2;
int[] dp = new int[99990000];
for(int i = 0; i < nums.length; ++i) {
for(int j = half_sum; j >= nums[i]; --j) {
dp[j] = Math.max(dp[j], dp[j-nums[i]]+nums[i]);
}
}
System.out.print(sum-2*dp[half_sum]);
}
}
试题 E: 斐波那契数列最大公约数
斐波那契数列满足 F1 = F2 = 1,从 F3 开始有 Fn = Fn?1+Fn?2 。请你计算GCD(F2020 ,F520),其中GCD(A, B) 表示 A 和 B 的最大公约数。
答案:6765
import java.math.BigInteger;
public class Main {
public static BigInteger gcd(BigInteger a,BigInteger b) {
return b.equals(BigInteger.ZERO) ? a : gcd(b, a.mod(b));
}
public static void main(String[] args) {
BigInteger arr[] = new BigInteger[2021];
arr[1] = arr[2] = BigInteger.ONE;
for(int i = 3; i <=2020; ++i) {
arr[i] = arr[i-1].add(arr[i-2]);
}
System.out.print(arr[2020].gcd(arr[520]));
}
}试题 F: 分类计数
输入一个字符串,请输出这个字符串包含多少个大写字母,多少个小写字母,多少个数字。
【输入格式】
输入一行包含一个字符串。
【输出格式】
输出三行,每行一个整数,分别表示大写字母、小写字母和数字的个数。
【样例输入】
1+a=Aab
【样例输出】
? 1
? 3
? 1?
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
String str = s.next();
char[] arr = str.toCharArray();
int upper = 0, lower = 0, digit = 0;
for(int i = 0; i < arr.length; ++i) {
if(arr[i] >= 'A' && arr[i] <= 'Z') {
upper++;
} else if(arr[i] >= 'a' && arr[i] <= 'z'){
lower++;
} else if(arr[i] >= '0' && arr[i] <= '9') {
digit++;
}
}
System.out.print(upper+"\n"+lower+"\n"+digit);
s.close();
}
}
试题 G: 八次求和
【问题描述】
给定正整数 n, 求 1^8 + 2^8 + ··· + n^8 mod 123456789 。其中 mod 表示取余。
【输入格式】
输入的第一行包含一个整数 n。
【输出格式】
输出一行,包含一个整数,表示答案。
【样例输入】
? 2
【样例输出】
? 257
【评测用例规模与约定】
? 对于 20% 的评测用例,1 ≤ n ≤ 20。
? 对于 60% 的评测用例,1 ≤ n ≤ 1000。
? 对于所有评测用例,1 ≤ n ≤ 1000000。
快速幂运算(算乘法的时间复杂度为logn)+模运算
import java.util.Scanner;
public class Main {
static int mod = 123456789;
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int n = s.nextInt();
long ans = 0;
for(long i = 1; i <= n; ++i) {
ans = (ans+quickPow(i,8))%mod; //long型的i防止计算时溢出
}
System.out.print(ans);
s.close();
}
static long quickPow(long a, int b) {
long ans = 1;
while(b>0) {
if((b&1) == 1) {
ans = (ans*a)%mod;
}
a = (a*a)%mod; //记录位权
b >>= 1;
}
return ans;
}
}BigInteger类
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
public static final BigInteger mod = BigInteger.valueOf(123456789);
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int n = s.nextInt();
BigInteger sum = BigInteger.ZERO;
for(int i = 1; i <= n; ++i) {
BigInteger temp = BigInteger.valueOf(i);
sum = sum.add(temp.multiply(temp).multiply(temp).multiply(temp)
.multiply(temp).multiply(temp).multiply(temp).multiply(temp));
}
System.out.print(sum.mod(mod));
s.close();
}
}