[Java知识库]心得体会day33(日撸 Java 三百行)

文章链接：日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客

Day33 图的广度优先遍历

33.1 思路：

结合下图，广度优先遍历假设从a节点出发，a访问后，访问领接点b/c,b访问了再访问c,又接着访问b的领接点，c的领接点，这样一层一层的访问，这就好比树的层次遍历一样。在访问图时要借助一个队列来实现

如图广度优先遍历的一种顺序是：a->b->c->d->e

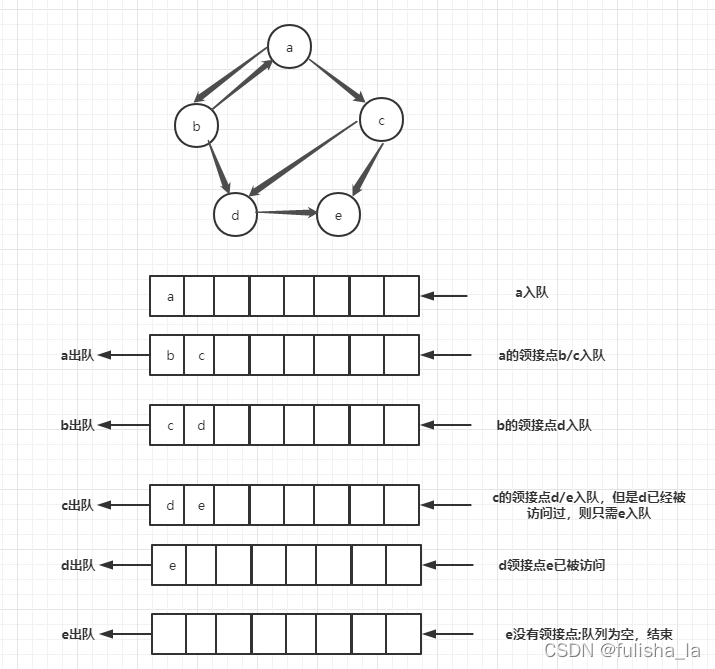
33.2 代码实现

结合上面的思路和文章来敲代码，在这段代码中，正如文章所说矩阵只要准备好了，写这些代码真的很方便。我感受最深的是：找节点的邻接点，这一行代码就可以去判断节点的领接点。

connectivityMatrix.getData()[tempIndex][i] == 0

    /**
     *  Breadth first traversal. paraStartIndex The start index.
     * @param paraStartIndex
     * @return
     */
    public String breadthFirstTraversal(int paraStartIndex) {
        CircleQueue tempQueue =  new CircleQueue();
        String resultString = "";

        int tempNumNodes = connectivityMatrix.getRows();
        boolean[] tempVisitedArray = new boolean[tempNumNodes];

        //Initialize the queue
        tempVisitedArray[paraStartIndex] = true;
        resultString += paraStartIndex;
        tempQueue.enqueue(new Integer(paraStartIndex));

        //Now visit the rest of the graph
        int tempIndex;
        Integer tempInteger = (Integer) tempQueue.dequeue();
        while (tempInteger != null) {
            tempIndex = tempInteger.intValue();

            //Enqueue all its unvisited neighbors.
            for (int i = 0; i < tempNumNodes; i++) {
                if (tempVisitedArray[i]) {
                    continue;
                }

                //Not directly connected
                if (connectivityMatrix.getData()[tempIndex][i] == 0) {
                    continue;
                }

                //Visit before enqueue.
                tempVisitedArray[i] = true;
                resultString += i;
                tempQueue.enqueue(new Integer(i));
            }

            //Take out one from the head.
            tempInteger = (Integer)tempQueue.dequeue();
        }

        return resultString;
    }

结合单元测试的例子画的图如下：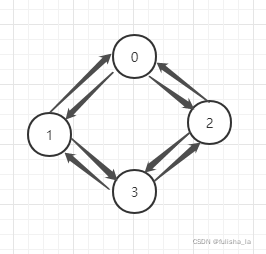

This is the connectivity matrix of the graph.
[[0, 1, 1, 0], [1, 0, 0, 1], [1, 0, 0, 1], [0, 1, 1, 0]]
No element in the queue
The breadth first order of visit: 2031

33.3 判断联通性

在今天的文章中，这个遍历只能遍历连通图(有向图)，若是非连通图，则会漏一些节点数据（需要加一个循环来验证节点是否访问完）。在代码中有一个布尔类型数组：boolean[] tempVisitedArray = new boolean[tempNumNodes];若我们在一次广度遍历完遍历这个tempVisitedArray数组，再循环遍历是否有false，若有则说明图是非连通图，这是我们还需要把未遍历的节点再遍历完。我自己写了一个判断连通，这里传了一个参数，为了方便，没有将这个数组设置为成员变量，仅仅只是做了一个测试。

    /**
     * Judge connectivity
     * @param tempVisitedArray bool类型 数组
     * @return
     */
    public boolean isConectivity(boolean[] tempVisitedArray) {
        int tempNumNodes = connectivityMatrix.getRows();
        for (int i = 0; i < tempNumNodes; i++){
            if (!tempVisitedArray[i]){
                System.out.println("The graph is not connectivity, The node is " + i);
                return false;
            }
        }
        return true;
    }

测试 1：?将测试的领接矩阵改为如下图所示的非连通图，则会发现打印的遍历会少打印

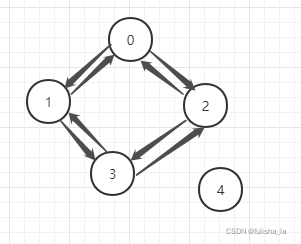
This is the connectivity matrix of the graph.
[[0, 1, 1, 0, 0], [1, 0, 0, 1, 0], [1, 0, 0, 1, 0], [0, 1, 1, 0, 0], [0, 0, 0, 0, 0]]
No element in the queue
The graph is not connectivity, The node is 4  //则是未被访问的节点 则图为非连通
The breadth first order of visit: 2031

测试2： (这里考虑的是无向图)

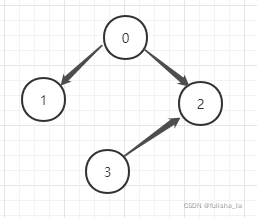
This is the connectivity matrix of the graph.
[[0, 1, 1, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 1, 1, 0]]
No element in the queue
The graph is not connectivity, The node is 3
The breadth first order of visit: 012

总结：

今天主要学习了图的遍历之广度优先遍历算法，结合day32利用矩阵运算可以判断图的连通性，则今天的广度优先遍历算法也可以判断图的连通性，我们只需要再借助一个bool类型的数组即可