[Java知识库]哈工大2022软件构造Lab1

说明

此博客内容为哈工大2022春季学期软件构造Lab1:Fundamental Java Programming and Testing，文章为个人记录，不保证正确性，仅供练习和思路参考，请勿抄袭。实验所需文件可以从这里获取（若打不开可以复制到浏览器）。
实验环境：IntelliJ IDEA 2022.1(Ultimate Edition)

一、Magic Squares

给定一个矩阵，判断其是否是一个幻方。矩阵以文件形式给出，同一行数字之间用制表符分隔。幻方需要满足：
（1）它是一个$n$阶方阵，且元素均为正整数；
（2）它的每行之和、每列之和、主副对角线之和相等。

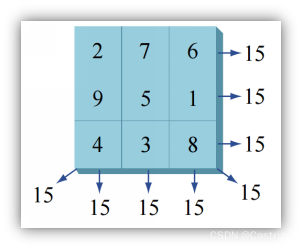
注意：当遇到文件数据不符合定义（如行列数不相等，不是矩阵，数字不是正整数，数字之间不以制表符分隔等），需要返回false并在控制台输出错误信息。

函数原型

static boolean isLegalMagicSquare(String filename) throws FileNotFoundException {
}

文件输入并检查

int row = 0,col = 0;
ArrayList<String> nums;
ArrayList<ArrayList<Integer>> matrix = new ArrayList<ArrayList<Integer>>();
Scanner input = new Scanner(new File(filename));

while(input.hasNextLine()) {
    nums = new ArrayList<String>(List.of(input.nextLine().split("\t")));

    if(col == 0) col = nums.size();
    else if(col != nums.size()) {
        System.out.println("The column of the rows are not equal!(Or, the numbers are not divided by '\\t')");
        return false;
    }
    try {
        for (int i = 0; i < nums.size(); i++) {
        	int value = Integer.parseInt(nums.get(i));
            matrix.get(row).add(value);
            if(value <= 0) {
                System.out.println("One of the numbers in the matrix is not a positive integer!");
                return false;
           	}
        }
    } catch(NumberFormatException e) {
        System.out.println("One of the numbers in the matrix is not an integer!");
        return false;
    }
    row++;
}
if(row != col) {
    System.out.println("The row of the matrix and the column are not equal!");
}

判断幻方

int sum = 0,sum1 = 0, sum2 = 0, sum_diag1 = 0, sum_diag2 = 0;

for(int i = 0; i < row; i++) {

    sum1 = sum2 = 0;
    sum_diag1 += matrix.get(i).get(i);
    sum_diag2 += matrix.get(i).get(row - i - 1);
    for(int j = 0; j < col; j++) {
        sum1 += matrix.get(i).get(j);
        sum2 += matrix.get(j).get(i);
    }

    if(sum == 0) sum = sum1;
    if(sum1 != sum2) return false;
    if(sum1 != sum) return false;
}
//判断对角线
if(sum_diag1 != sum_diag2 || sum_diag1 != sum) return false;

return true;

二、Turtle Graphics

原实验为MIT的实验。
任务：
下载turtle相关类，放于P2包中。实现TurtleSoup中的各个方法，控制turtle绘制图案并通过JUnit中的测试。下面对于git部分的problem不加以说明。
*注意：由于要把Turtle放入P2包中，Turtle中package需要加上P2。

package P2.turtle;

Problem 3

调用已经实现的forward和turn函数，实现TurtleSoup.java中的drawSquare方法，在main函数中测试其功能。

函数原型

//已经被实现，使turtle向前走units个单位
public void forward(int units) {
}
//已经被实现，使turtle顺时针转弯degrees度（角度制）
public void turn(double degrees) {
}
//需要实现
public static void drawSquare(Turtle turtle, int sideLength) {
}

实现

实现很简单，只需要向前走sideLength,转弯90°即可。

public static void drawSquare(Turtle turtle, int sideLength) {
    for(int i = 0; i < 4; i++) {
        turtle.forward(sideLength);
        turtle.turn(90);
    }
}

Problem 5

用turn和forward实现画正多边形的三个方法，并通过JUnit的测试。

函数原型

//给定正多边形边数，计算其内角角度
public static double calculateRegularPolygonAngle(int sides) {
}
//给定正多边形角度，计算其边数
public static int calculatePolygonSidesFromAngle(double angle) {
}
//画正多边形
public static void drawRegularPolygon(Turtle turtle, int sides, int sideLength) {
}

实现

思维难度不高，用初中数学知识算一下就行。

public static double calculateRegularPolygonAngle(int sides) {
    return 180.0 - 360.0 / sides;
}
//为了保证准确度，四舍五入
public static int calculatePolygonSidesFromAngle(double angle) {
    return (int)Math.round(360 / (180 - angle));
}
public static void drawRegularPolygon(Turtle turtle, int sides, int sideLength) {
    double angle = calculateRegularPolygonAngle(sides);
    for(int i = 0; i < sides; i++) {
        turtle.forward(sideLength);
        turtle.turn(180 - angle);
    }
}

JUnit单元测试

在IDEA下若TurtleSoupTest.java报错，在提示的窗口中自动fix下载即可。
测试方法：实现方法后，在TurtleSoup.java中的对应测试旁点击小箭头后直接运行该测试。


测试通过：

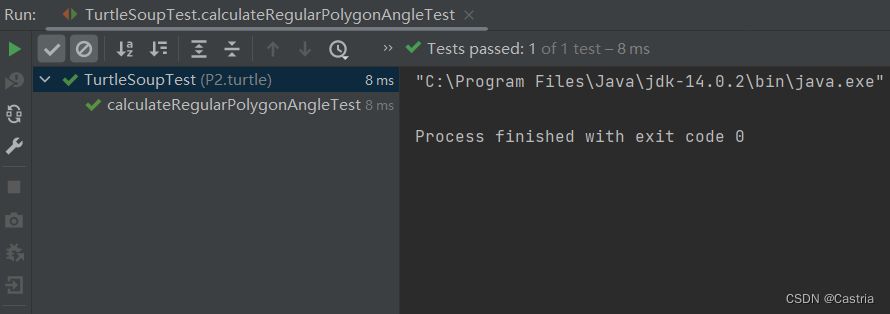
Problem 6

实现方法calculateBearingToPoint和calculateBearings，并通过JUnit测试。

calculateBearingToPoint方法：
给定当前朝向（以正北方向为0°，顺时针方向），坐标和目的地，计算旋转角度的大小（始终向顺时针旋转，旋转角度在$[0,360°)$中）
calculateBearings方法：
给定两个List xCoords和yCoords，分别含有一系列横坐标和纵坐标，且个数相同（记为$n$）；设最初turtle的朝向为正北并在(xCoords[0], yCoords[0])处，计算$n?1$次转向的角度。当$n==0$，返回空列表。

函数原型

public static double calculateBearingToPoint(double currentBearing, int currentX, int currentY,
                                             int targetX, int targetY) {
}

实现

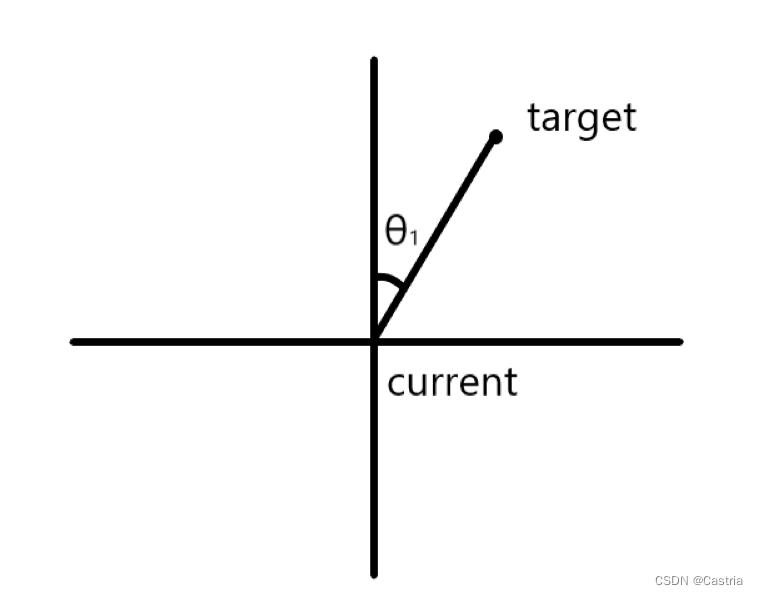
对于每个target坐标，先计算它相对于当前位置的偏转角${\theta }_1$（代码中的targetBearing），可以通过Math库中的反三角函数实现(弧度制要转化成角度制)；此外，由于反三角函数返回$[?\frac{\pi }{2},\frac{\pi }{2}]$中的值，无法区分$30°$和$150°,$需要判断一下target的相对位置（在current的上方还是下方，注意坐标轴的情况）

public static double calculateBearingToPoint(double currentBearing, int currentX, int currentY,
                                             int targetX, int targetY) {
    double deltaX = targetX - currentX;
    double deltaY = targetY - currentY;
    double dist = Math.sqrt(deltaX * deltaX + deltaY * deltaY);

	//相同点, return 0.0
    if(dist == 0) return 0;
    double targetBearing = Math.toDegrees(Math.asin((targetX - currentX) / dist));
    if(targetX >= currentX) { // right
        if(targetY < currentY) { // right, down
            targetBearing = 180 - targetBearing;
        }
        /*
        特殊情况:
        when theta == 0, asin = 0;
        when theta == 90, asin = 1;
        when theta == 180, asin = 0.
        */
    }
    else {
    	/*
    	特殊情况:
    	when theta == 270, asin = -1.(180 - (-90) = 270)
    	*/
        if(targetY <= currentY) {
            targetBearing = 180 - targetBearing;
        }
        else {
            targetBearing = 360 - targetBearing;
        }
    }
    
    targetBearing -= currentBearing;
    //由于只能顺时针转，对两角之差的正负讨论一下
    return targetBearing >= 0? targetBearing: targetBearing + 360;
}

calculateBearings用calculateBearingToPoint很好实现。记录当前位置和朝向，不断调用calculateBearings即可。
*List是抽象类，需要返回其子类ArrayList。

public static List<Double> calculateBearings(List<Integer> xCoords, List<Integer> yCoords) {
    if(xCoords.size() == 0) {
        return new ArrayList<>();
    }
    ArrayList<Double> ld = new ArrayList<Double>();
    int currentX = xCoords.get(0), currentY = yCoords.get(0);
    double currentBearing = 0;
    for(int i = 1; i < xCoords.size(); i++) {
        currentBearing = calculateBearingToPoint(currentBearing, currentX, currentY, xCoords.get(i), yCoords.get(i));
        ld.add(currentBearing);
        currentX = xCoords.get(i);
        currentY = yCoords.get(i);
    }
    return ld;
}

Problem 7

实现convexHull方法（计算点集的凸包），并通过JUnit测试。文件中提示了一种Gift-wrapping算法($O(n^2)$)；由于篇幅较长，另一种算法（Graham扫描法,$O(nlogn)$）单独放在了我的另一篇博客中。

Problem 8

用前面实现的方法绘制自己的Personal Art，由于是开放式问题整活的机会 ，略去。

三、Social Network

实现FriendshipGraph和Person类，其中FriendshipGraph应该有方法addVertex(加点)，addEdge(加单向边)，getDistance(返回二人最短距离，若不连通返回-1)；Person类有一个String型的name成员。

Person类

简单地设置一下构造函数和getter/setter。

public class Person {
    private String name;

    public Person(String name) {
        this.name = name;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

}

FriendshipGraph类

addVertex方法

这里采用邻接表存图：用一个从Person到ArrayList<Person>的HashMap。

private HashMap<Person, ArrayList<Person>> adjList;
//构造方法
public FriendshipGraph() {
    adjList = new HashMap<Person, ArrayList<Person>>();
}
public void addVertex(Person p) {
    if(!adjList.containsKey(p)) {
        adjList.put(p, new ArrayList<Person>());
    }
    else {
        System.out.println("There is already a person named " + p.getName() + "!");
    }
}

addEdge方法

直接在邻接表中添加对应项即可。这里没有判断重边：邻接表判断重边需要$O(n)$时间，重边也不影响getDistance的结果。

public void addEdge(Person from, Person to) {
    if(!adjList.containsKey(from)) {
        System.out.println("There is no person named " + from.getName() + "!");
        return;
    }
    adjList.get(from).add(to);
}

getDistance方法

直接进行一次BFS即可。这里用了一个私有内部类pair来记录到当前状态步数。

public int getDistance(Person from, Person to) {
    if(!adjList.containsKey(from)) {
        System.out.println("There is no person named " + from.getName() + "!");
    }
    if(!adjList.containsKey(to)) {
        System.out.println("There is no person named " + to.getName() + "!");
    }

	//队列
    LinkedList<pair> Q = new LinkedList<pair>();
    //记录是否访问过
    HashMap<Person, Boolean> visit = new HashMap<Person, Boolean>();
    
    //从第一个人开始，步数为0
    Q.add(new pair(from, 0));
        
    while(!Q.isEmpty()) {
        pair now = Q.pollFirst();
        visit.put(now.getPerson(), true);
        if(now.equals(to)) {
            return now.getStep();
        }
        for(Person p: adjList.get(now.getPerson())) {
            if(!visit.containsKey(p)) {
                Q.add(new pair(p, now.getStep() + 1));
            }
        }
    }

    return -1;
}

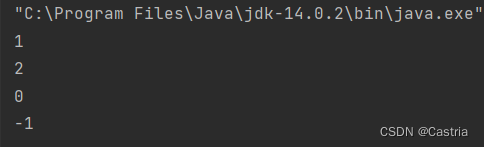
运行结果

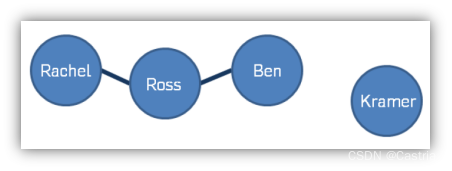
public static void main(String[] args) {
    FriendshipGraph graph = new FriendshipGraph();
    Person rachel = new Person("Rachel");
    Person ross = new Person("Ross");
    Person ben = new Person("Ben");
    Person kramer = new Person("Kramer");
    graph.addVertex(rachel);
    graph.addVertex(ross);
    graph.addVertex(ben);
    graph.addVertex(kramer);
    graph.addEdge(rachel, ross);
    graph.addEdge(ross, rachel);
    graph.addEdge(ross, ben);
    graph.addEdge(ben, ross);
    System.out.println(graph.getDistance(rachel, ross));//should return 1
    System.out.println(graph.getDistance(rachel, ben));//should return 2
    System.out.println(graph.getDistance(rachel, rachel));//should return 0
    System.out.println(graph.getDistance(rachel, kramer));//should return -1
}

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖